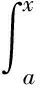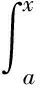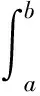离散化方法在积分中的应用
李排昌,王铁英
(中国人民公安大学网络安全保卫学院,北京 100038)
0 引言
定义1 数学上涉及点的结构的范畴,称为微观数学。
定义2 数学上不涉及点的结构的范畴,称为宏观数学。
在数学中,点是构成图形的基本单元,点动成线,线动成面。曲线、曲面都是宏观意义下的几何形状,曲线的长度、曲边梯形的面积都是宏观意义下的数学问题。点在宏观意义下既没有大小也没有长度。宏观上实数轴上的有理点是密集的,即宏观上我们看不到所谓相邻的有理点。假如承认实数轴上的有理点是离散的,即承认上数轴上有相邻的有理点且相邻点与点之间有间隔距离,则在宏观意义下的连续曲线,其自变量为有理点所对应的图形在宏观意义下仍是连续曲线,在微观意义下实际却是散点图。这就是所谓微观数学,用这种观点分析解决积分问题,我们称之为积分的离散化处理。
1 区间[0,1]内有理点的密集性与离散性
设R01为[0,1]区间内的有理数集合,由于R01是可数点集,故R01中的有理数可排成一个无穷序列
R01∶x1,x2,…,xn,…。
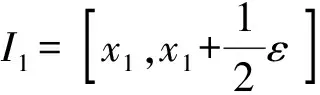
由于[0,1]区间的长度是1,而ε<1,从区间覆盖的结论看,这个区间序列I1,I2,…,In,…显然不能完全覆盖[0,1]区间,否则,这个区间序列的总长度就会大于1。由此可知,这个区间序列I1,I2,…,In,…中必然有某些区间仅套住R01内唯一的一个点,即R01内的有理点可以用不相交的区间分离开来。这就是所谓R01微观上离散。这使我们不得不承认R01内有相邻点(两个有理数之间不再有其他有理数),且相邻两点之间有间隔距离,我们把这个间隔距离记为dx,并称为一个有理数点的占位长度(引入点有占位长度与R01宏观上密集性并不矛盾)。由于[0,1]区间内有理数点的密集性,dx既不是宏观意义下的0.1也不是0.01,它在宏观意义下是0,但微观上并不是0。[0,1]区间内所有有理数点占位长度的对接长度是1。在微观意义下,n→∞时In的长度|In|甚至比dx还小,小到连一个有理数点的占位长度都盖不住,才不发生区间相交的情况,这个区间序列I1,I2,…,In,…的总长度才可以小于任意给定的正数ε。值得注意的是,宏观意义下并不能解释dx的存在与大小,因为不能解释从哪个n开始,区间In才仅套住唯一的一个有理数点。
命题1:R01宏观上是密集的,微观上是离散的,有理数点的占位长度是客观存在的。
同理可得,任何区间[a,b]内的有理点集宏观上是密集的,微观上是离散的。
2 离散化方法在定积分中的应用
我们首先通过一个面积实例引入定积分的定义,并对连续变量的离散化方法在积分中的应用进行论述和说明,逐步揭示积分的奥秘。
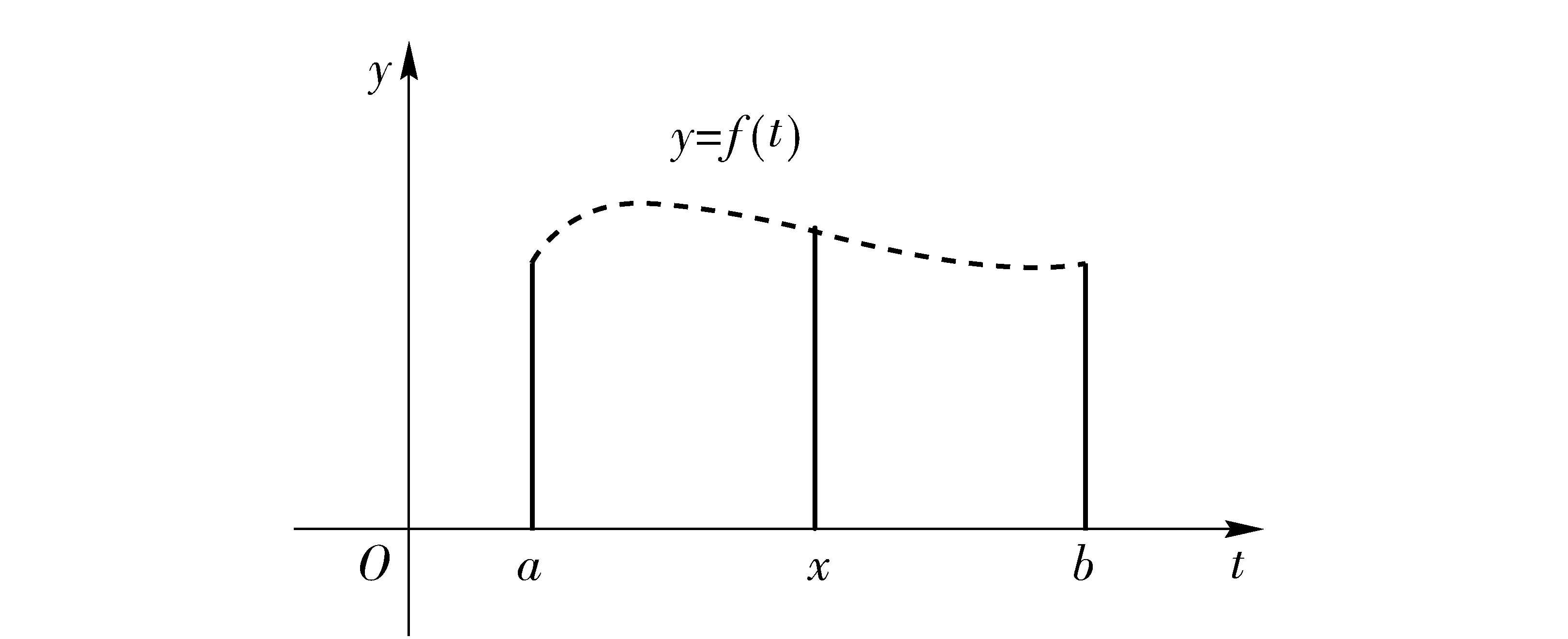
例1(曲边梯形面积的经典实例) 设函数y=f(x)≥0在[a,b]区间上连续。曲线y=f(x)与直线x=a、x=b及x轴围成曲边梯形(见图1),求曲边梯形的面积S。
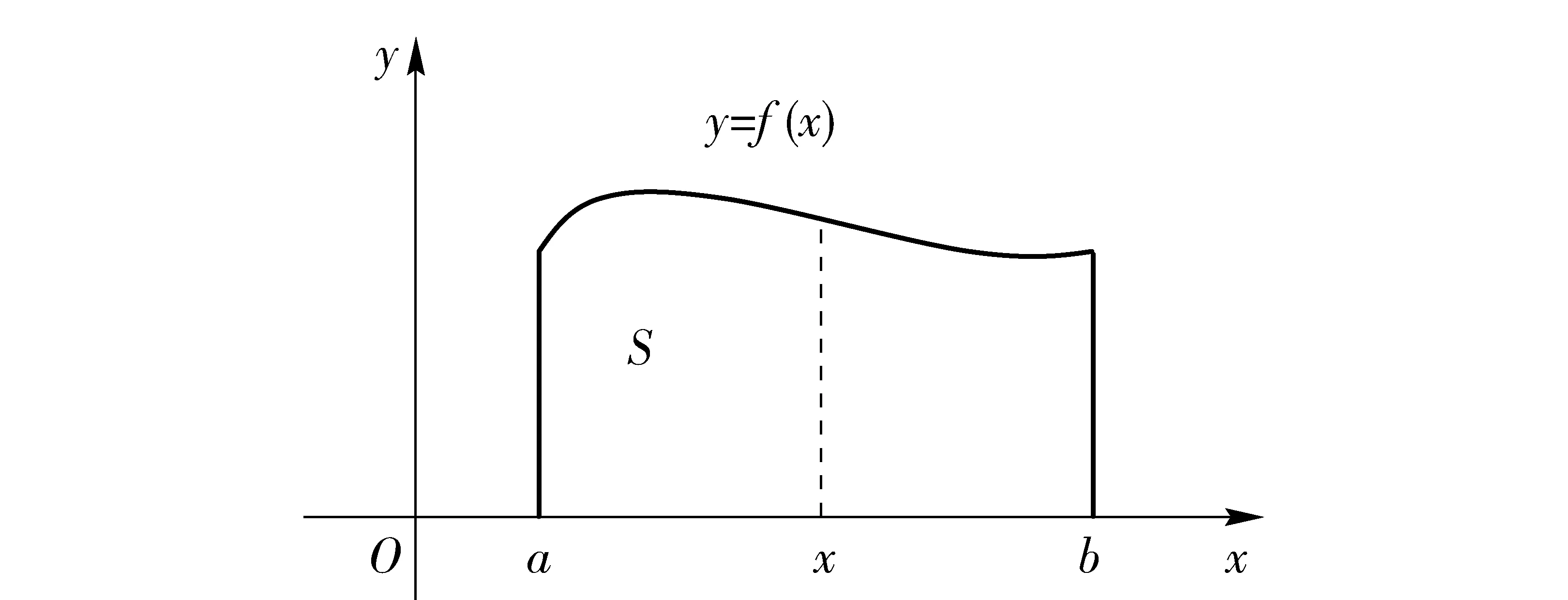
图1
解:显然,所求面积客观存在。区间[a,b]内的每个有理点x唯一对应曲边上的一点M(x,f(x))。由于区间[a,b]内的有理点是密集的,其自变量为有理点所对应的图形在宏观意义下仍是连续曲线,在微观意义下是散点图(见图2)。在区间[a,b]上,对于每个有理点x,有一个嵌于曲边梯形内的高为f(x)宽为dx(dx表示有理数点的占位长度)的微观矩形,其面积为f(x)dx,我们称之为占位面积(区别于宏观意义下的面积)。区间[a,b]内从a到b全部有理点所对应的微观矩形对接成宏观上的曲边梯形,而区间[a,b]内全部有理点所对应的微观矩形的占位面积对接后的面积正是曲边梯形的面积S。
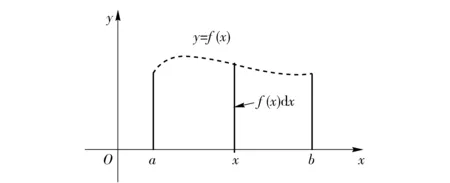
图2

当函数y=f(x)在[a,b]上连续时(目前仅讨论这种情况),其积分一定存在。函数y=f(x)在[a,b]上的积分,其几何意义表示占位微元f(x)dx对应的微观图有序对接后所形成的平面图形的面积或面积的代数和。积分是一种新的求和方式,其求和范围是[a,b]上的全部有理点,我们称积分为对接和。占位微元f(x)dx的引入为解决实际问题时构造被积函数提供了理论依据,它不同于现行积分理论中微元法的微元。这是用连续变量的离散化方法解决积分问题。我们不再用分割、求和、取极限的定义和方法处理定积分。
设函数f(x)、g(x)在[a,b]上连续,由定积分的定义容易证明积分具有下述7个性质:


(3) 若f(x)≥0,从而f(x)dx≥0,则
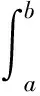
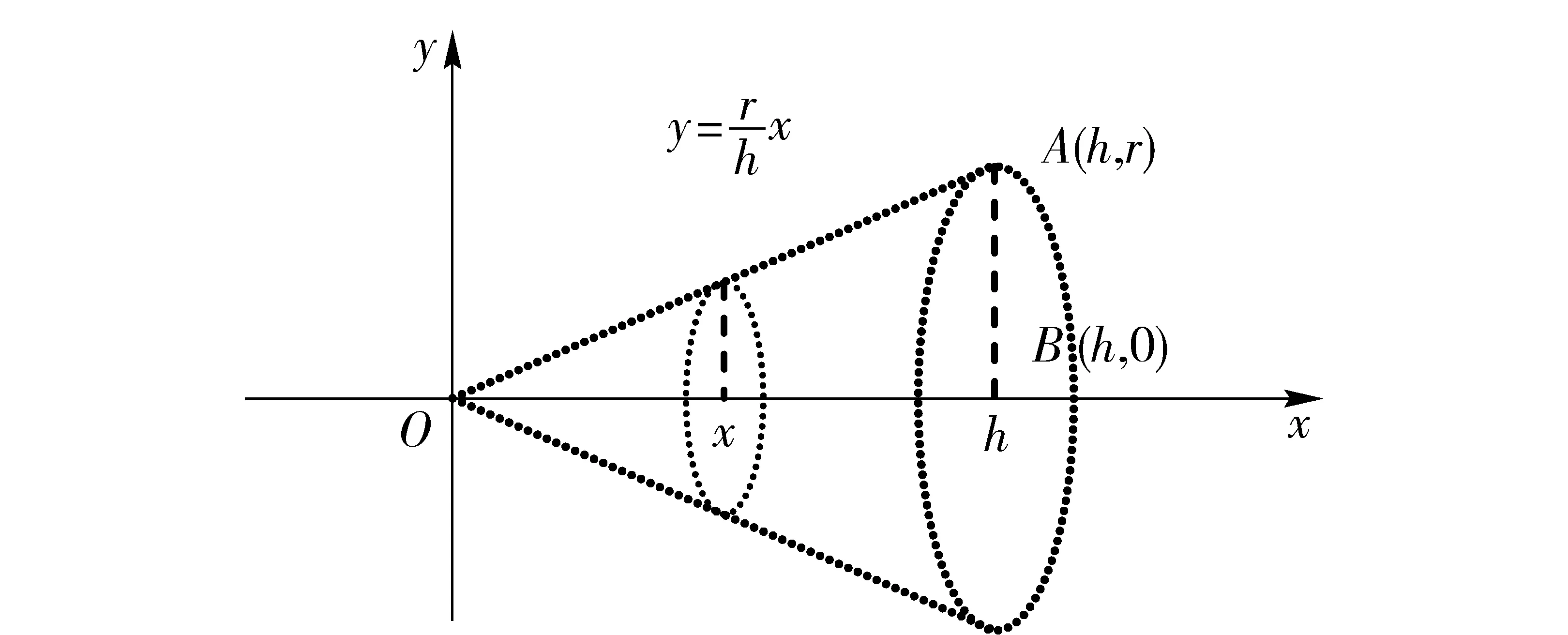
(4) 设a 由积分的几何意义,这4个性质显然成立。 证明:只证明f(x)+g(x)的情况。由积分的几何意义,当f(x)≥0、g(x)≥0或f(x)≤0、g(x)≤0时,结论显然成立。对于一般情况,由于f(x)、g(x)是连续函数,则f(x)+g(x)也连续。在区间[a,b]上,设f(x)的最小值是-m(m>0)、g(x)的最小值是-n(n>0)。此时,显然有: f(x)+m≥0,g(x)+n≥0。 由积分的几何意义得 (1) 另一方面,还有 (2) 比较上述(1)、(2)两式的左右两端;左端相等,故右端相等,所以 同理可证明其他情况。 由以上性质可得: (6) 若y=f(x)在区间[a,b]上的最小值是m、最大值是M,则 由性质(6)以及连续函数的介值定理可得积分中值定理: (7) 必有ξ∈[a,b],使得 图3 由积分的性质和导数的定义容易证明Φ′(x)=f(x),即Φ(x)恰好是f(x)的一个原函数。 由于f(x)的两个原函数之间仅差某一常数,因此,假设F(x)也为f(x)的一个原函数,则存在某一常数C使得 Φ(x)=F(x)+C, 由Φ(a)=0,可得C=-F(a),而 (3) 从而,所求积分为 (4) 公式(4)称为牛顿—莱布尼兹公式[1]223-242。 例2 (旋转体体积的经典实例) 求底半径为r、高为h的圆锥的体积V。 图4 解:我们建立如图4所示的坐标系,则圆锥是由平面直角三角形△OBA绕Ox轴旋转而成的旋转体。在微观数学意义下,区间[0,h]内每个有理点x处对应一个底半径为rx/h、厚度为dx的圆柱体,其体积为π(rx/h)2dx,我们称之为占位体积(区别于宏观意义下的体积),所有圆柱体的占位体积对接和就是圆锥的体积V,即圆锥的体积V是函数π(rx/h)2在区间[0,h]上的积分。所以 例3(曲线弧长的经典实例)设L∶y=f(x),x∈[a,b]是一条光滑的平面曲线。求曲线L的弧长[1]282-283s。 解:由于区间[a,b]内的每个有理点x唯一对应曲边上的一点M(x,f(x)),而且区间[a,b]内的有理点是密集的,其自变量为有理点所对应的图形在宏观意义下仍是连续曲线L,在微观意义下是散点图(见图5)。曲线上任意相邻两点P(x,f(x))、P1(x+dx,f(x+dx))的距离ds(称为占位长度)就是曲线上相邻两点曲线的弧长,曲线L的弧长s是曲线上相邻点的占位长度之和,也就是自变量为有理点所对应的散点图构成的折线总长。这是用连续变量的离散化方法解决积分中的曲线弧长问题。 由于曲线上的折线段与区间[a,b]内的有理点一一对应,故曲线的弧长为 (5) 例4 求曲线y=x2在区间[0,1]上一段的弧长。 解:由于y′=2x,由公式(5),曲线的弧长为 [1]同济大学数学系.高等数学[M].北京:高等教育出版社,2007:223-242;282-283.

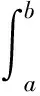
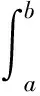
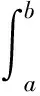
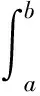
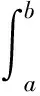
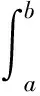
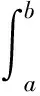
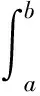
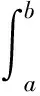
3 变上限函数与积分的计算