永磁同步电机一种新型滑模观测器的设计

徐雯静，宋蛰存

(东北林业大学 机电工程学院，哈尔滨 150040)

随着微处理器、电力电子技术、 现代控制理论以及高性能永磁材料的发展，永磁同步电机(PMSM)在工业上得到日益广泛的应用，如空调压缩机、电动自行车、洗衣机等。在PMSM自控变频调速系统中，转子位置信息是需要获得的，进行转子磁场定向控制时，坐标变换就需要提供精确的转子位置信息。通常，转子位置可以通过旋转变压器、光电编码器或其他类型的机械式传感器直接测量计算得到，但这些传感器由于其成本、维护量以及稳定性等原因而往往不被实际控制系统所采纳。无传感控制的概念出现在20世纪70年代，其在PMSM转子位置及转速估算方面取得了不断的发展。无传感控制的基本原则是通过使用包括直接计算、参数辨识、条件估算和间接测量等手段方式推断出转子位置和速度，定子电流和电压通常用来计算转子位置和转速信息[1-4]。

基于滑模观测器(SMO)的PMSM无位置传感控制技术的研究始于20世纪90年代[5]，滑模是一个非线性的概念，其利用合适的切换率可以控制系统在两个结构中切换，目的是令系统收敛于滑模平面。对于在PMSM控制系统中的SMO来说，通过一些可测量参数去估算未知参数是其目的所在。由于SMO对精确的模型及参数的不敏感特性，使其拥有很强的鲁棒性。

本文设计了一种新型滑模观测器来估算转子位置，用于实现PMSM的无位置传感矢量控制。基于文献[6-8]，新型滑模观测器主要包括对滑模电流观测器模型的设计和对反电势滤波器的设计。在分析PMSM数学模型的基础上，建立了基于新型滑模观测器的PMSM无位置传感矢量驱动系统，并通过对一定转速下的PMSM进行相关测试，验证新型滑模观测器控制策略的实际性能。

1 新型滑模观测器的设计原理

1.1 滑模电流观测器模型的设计原理

PMSM在定子两相静止参考坐标系(α-β轴系)下的数学模型表示为：

(1)

式中：iα、iβ为α-β轴电流分量；uα、uβ为α-β轴电压分量；eα、eβ为α-β轴反电动势分量；Rs为定子相电阻；Ls为定子相电感；ωe为电角速度；ψf为磁链系数；θe为电机电角度。

考虑到滑模变结构控制理论和文献[9]中提出的滑模抖振问题，可以设计出一个基于饱和函数的新型滑模电流观测器为：

(2)

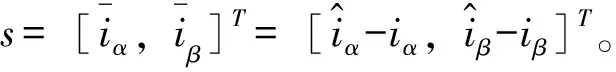
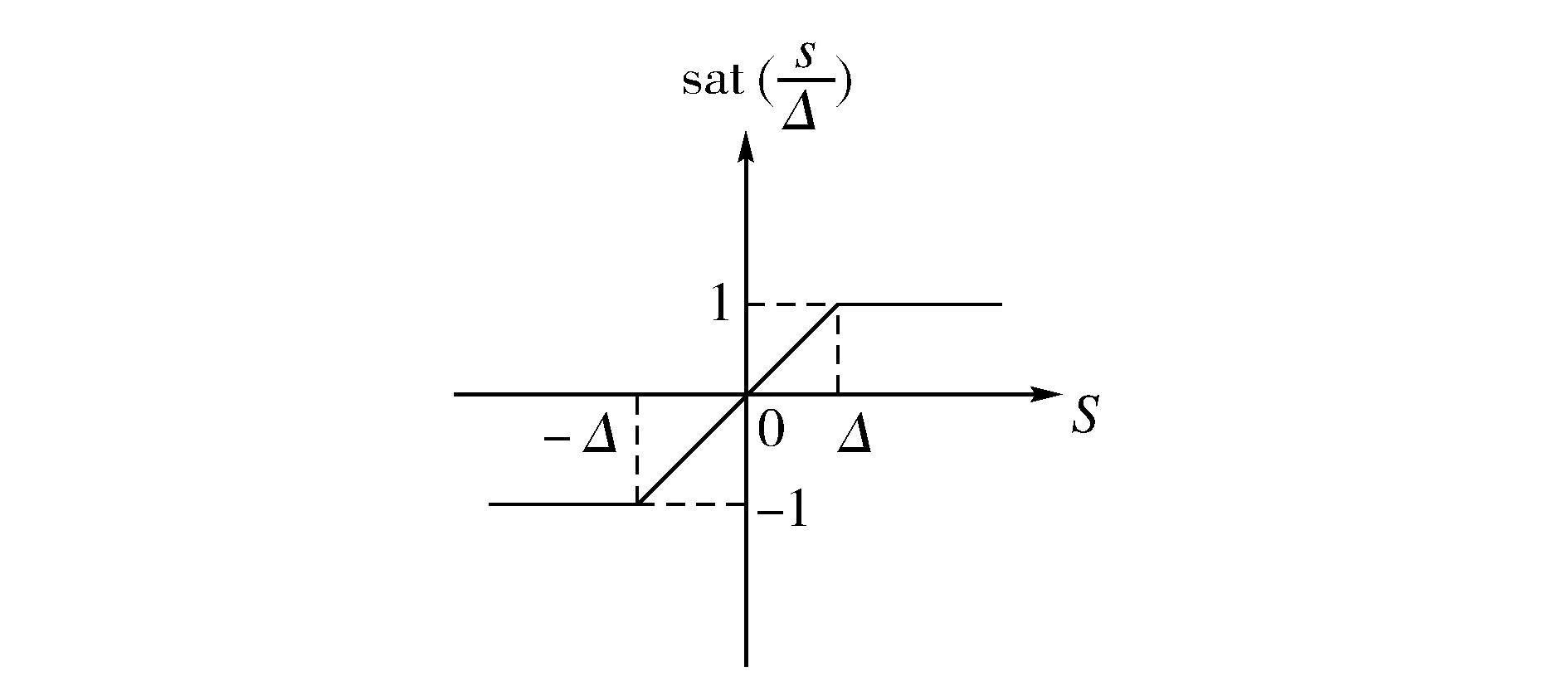
图1 饱和函数特性曲线

从图1可以看出，饱和函数下的变结构控制可形成三种变换结构，包含s=Δ、s=-Δ两个滑模面。饱和函数在-ΔΔ或s<-Δ以外则是传统的滑模继电型控制。对zα、zβ定义为：

(3)

式中：k为大于零的滑模增益系数，Δ此时为估算电流与实际电流之间的误差设定值；而公式(2)中，zeα、zeβ为滑模控制函数的等效控制函数，是由zα、zβ经过低通滤波处理获得，定义为：

(4)

由公式(1)、(2)可得所设计的新型滑模电流观测器的动态误差方程为：

(5)

(6)

得到由滑模控制函数和其等效控制函数组合构成的反电势原理框图如图2所示。

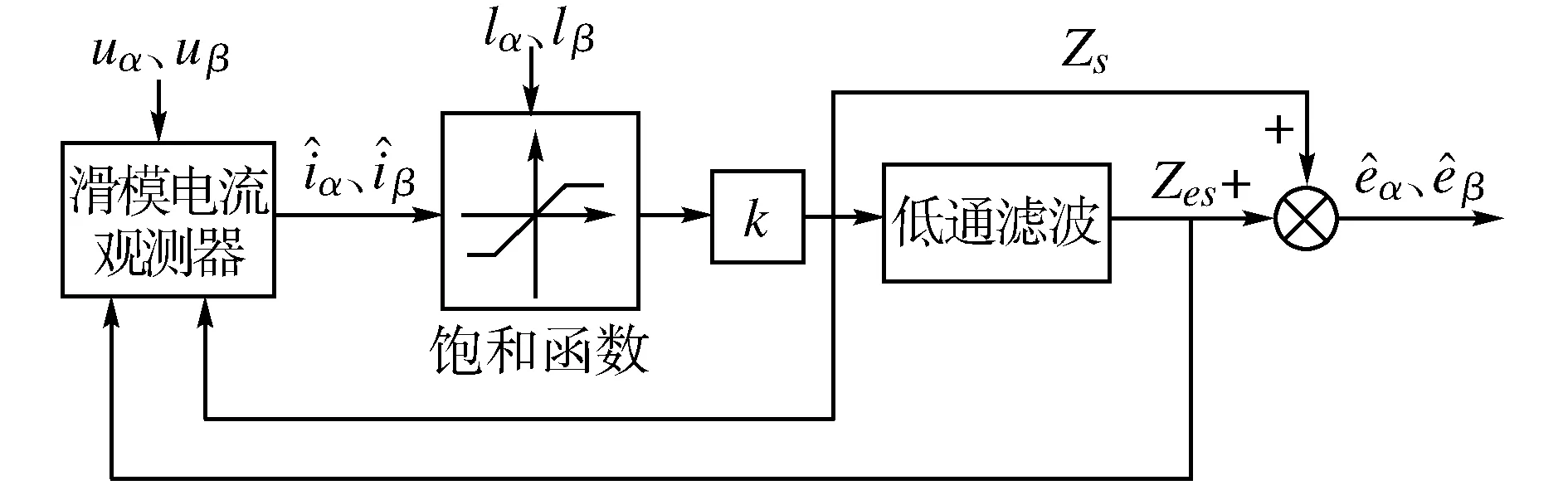
图2 反电势构成原理框图

由此，估算得到反电势信息之后，可利用公式(7)进行转子位置的计算：

(7)

1.2 稳定性分析

根据滑模变结构控制理论[10]，滑模观测器需要满足的稳定性条件为：

(8)

即得到：

(9)

(10)

即当k>max(|eα|/2,|eβ|/2)时，滑模观测器能够满足其稳定性条件。可以看出，相比传统滑模观测器而言，新型滑模观测器的滑模增益k扩大了其取值下限，即可以减小滑模增益k，同时对滑模抖振也会起到一定的抑制作用，从而使得电流能稳定输出。

1.3 反电势自适应滤波器的设计原理

反电势是用来估算转子位置的直接变量，但对于传统滑模观测器而言，控制函数采用开关符号函数时，由于滑模抖振作用较为剧烈，估算反电势将包含一定的高频抖动分量，这将直接影响到位置估算的精确性。设计的新型电流滑模观测器在一定程度上对抖振起到了削弱的作用，为了进一步提高反电势的估算精度，满足系统对高性能应用的要求，本文参考了文献[7～8]，设计了反电势自适应滤波器，来对反电势进行二次滤波处理，该滤波器具有扩展卡尔曼滤波结构：

(11)

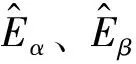
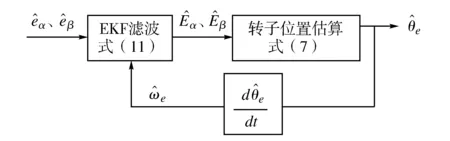
图3 反电势自适应滤波器原理图

2 系统仿真分析

根据前述所设计的新型SMO以及PMSM矢量驱动控制原理，对一台两对极表贴式永磁同步电机进行仿真实验，仿真电机参数见表1。

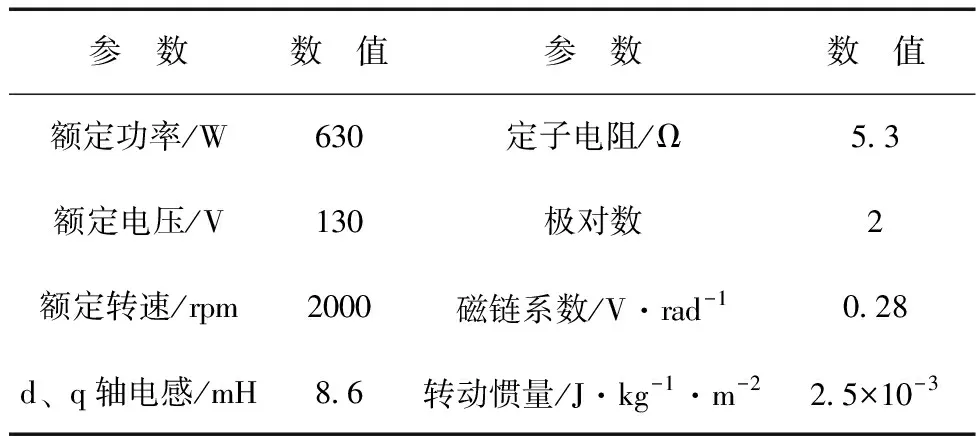
表1 仿真电机参数

如图4所示为建立的基于SMO的PMSM无位置传感矢量驱动系统模型，电流控制策略采取ID=0的控制，对应的Simulink系统仿真模型如图5所示。传统SMO和新型SMO可以在系统的滑模观测器(SMO)模块内部替换，以方便对比显示所设计的新型SMO具有的优越性能。

图4 基于新型SMO的PMSM矢量系统控制模型

如图6所示为比较传统SMO和新型SMO两种方法估算性能的相应仿真结果，包括估算反电势波形和估算转子位置局部放大波形，其中仿真电机给定转速为500r/min。可以看出，传统SMO估算出的反电势包含有一定的高频抖动分量，这是由于滑模固有的抖振作用所导致，该高频抖动分量通过反正切运算环节的除法运算被放大，致使估算转子位置产生较大的波动；而新型SMO由于采取了削弱抖振的设计措施，并且利用反电势自适应滤波器对估算反电势进一步加以滤波处理，使估算出的反电势无明显高频抖动分量，估算转子位置更为平滑。

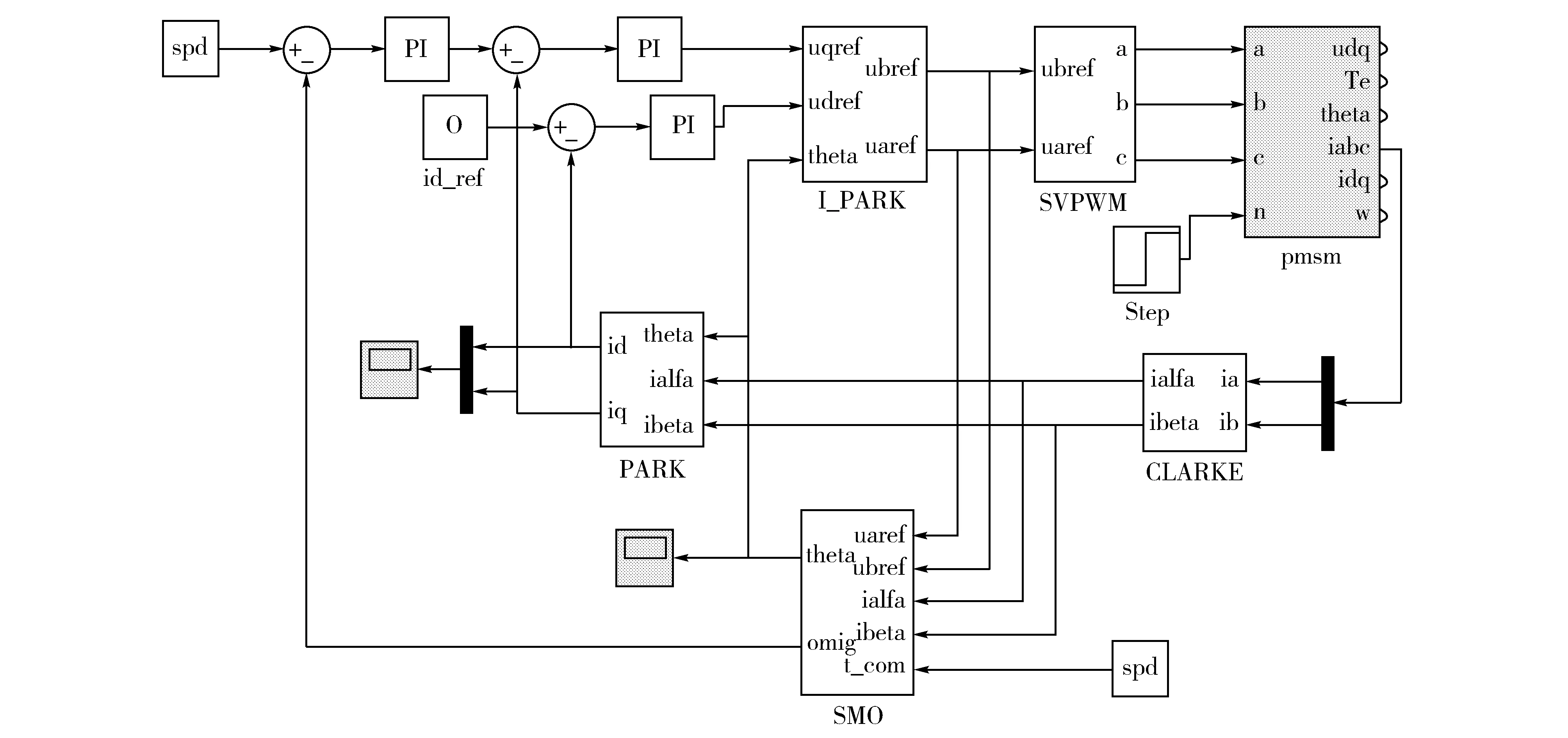
图5 基于新型SMO的PMSM矢量系统仿真模型

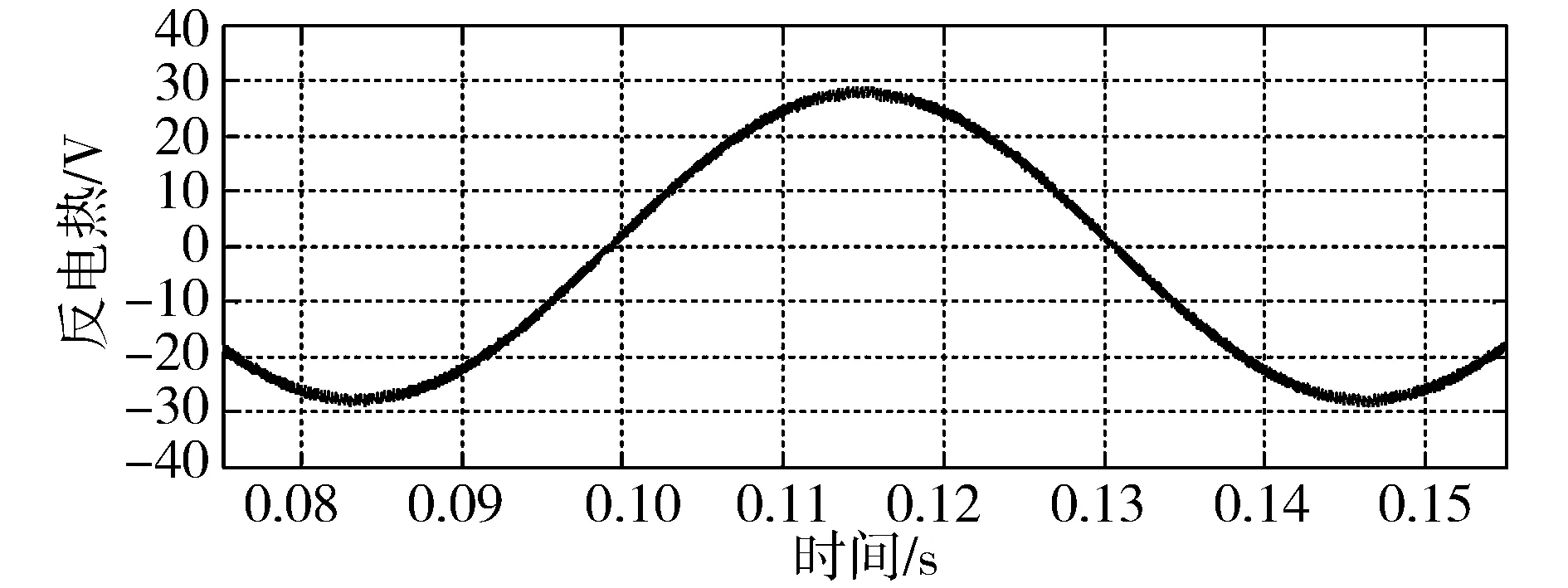
(a)传统SMO估算反电势波形

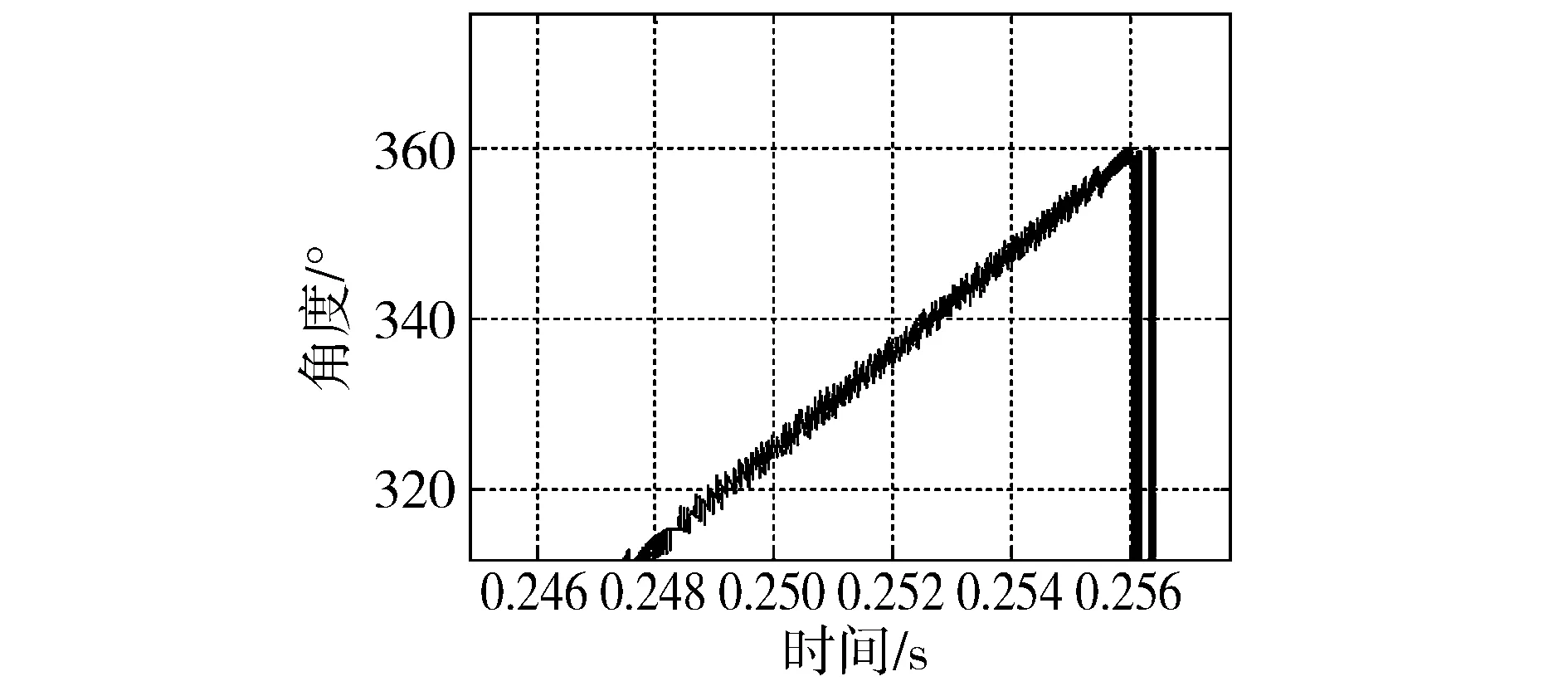
(b)传统SMO估算转子位置局部放大波

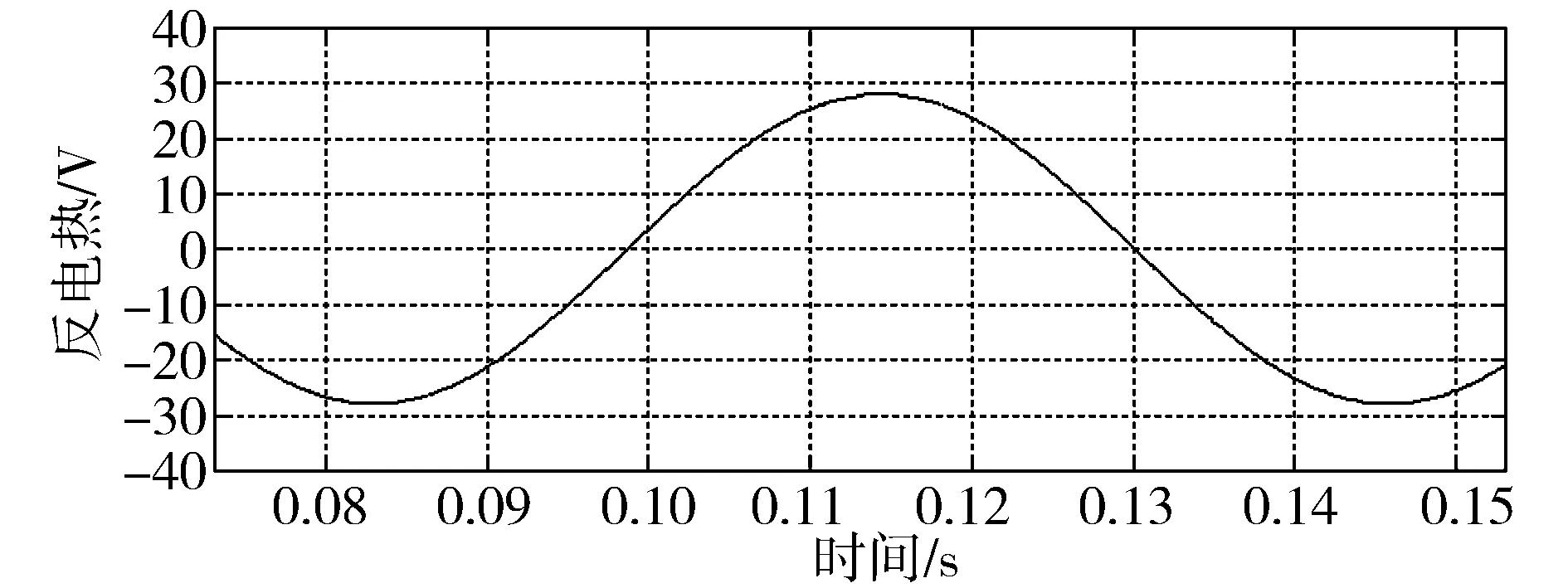
(c)新型SMO估算反电势波形

(d)新型SMO估算转子位置局部放大波形

3 系统实验分析

为验证所设计的新型SMO应用于实际的无位置传感PMSM矢量驱动系统时的正确性及可行性，搭建基于TMS320F2808 DSP的实验平台，对一台四对极表贴式PMSM进行实验验证。实验波形如图7和图8所示。

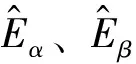
(a)f=12.5Hz

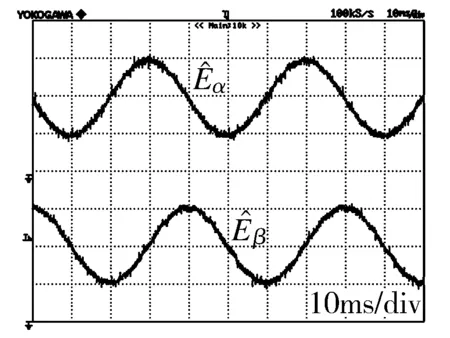
(b)f=25Hz

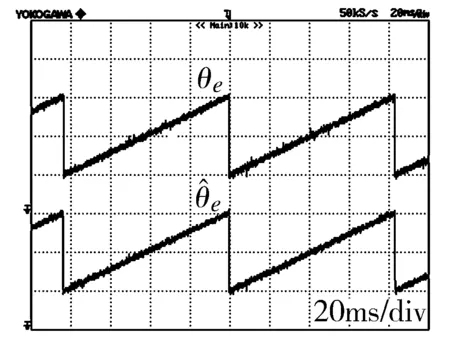
(a)f=12Hz

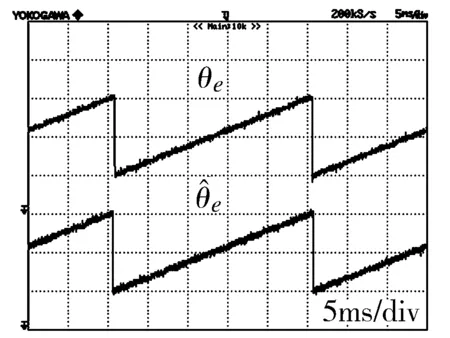
(b)f=40Hz

4 结束语

本文设计并实现了一种新型滑模观测器，设计内容包括电流观测器模型的设计、滑模控制函数的选取以及反电势自适应滤波器的设计。对新型滑模电流观测器的稳定性加以分析，所设计的新型滑模观测器对滑模抖振作用能够起到一定的抑制作用，并通过对反电势的滤波处理，使系统能够在提高反电势估算精度的同时，提高转子位置的估算精度。仿真实验验证了本文所设计的新型滑模观测器相比于传统滑模观测器，能够获得更高精度的反电势以及转子位置信息，并通过实验平台验证了新型滑模观测器应用在PMSM无位置传感矢量驱动系统中的正确性、可行性。

【参 考 文 献】

[1]梁 艳，李永东.无传感器永磁同步电机矢量控制系统概述[J].电气传动，2003(4)：4-9.

[2]李永东，张 猛.高性能交流永磁同步电机伺服系统现状[J].伺服控制，2008(1)：34-36.

[3]Proca A B，Keyhani A.Identification of variable frequency induction motor models from operating data[J].IEEE Trans.Electrical Energy，2002，17(1)：24-31.

[4]Lima F，Kaiser W，da Silva I N，et al.Speed neuro-fuzzy estimator applied to sensorless induction motor control.Latin Am.Trans[J].IEEE(Revista IEEE America Latina)，2012，10(5)：2065-2073.

[5]Utkin V，Guldner J，Shi J.Sliding Mode in Electromechanical Systems[M].New York：Taylor & Francis Group Press，1999.

[6]Lin F J，Chou W D.An induction motor servo drive using sliding-mode controller with algorithm[J].Electric Power Systems Research，2003，6(2)：93-108.

[7]Karanayil B，Rahman M F，Grantham C.Online stator and rotor resistance estimation scheme using artificial neural networks for vector controlled speed sensorless induction motor drive[J].IEEE Trans.Ind.Electron，2007，54(1)：167-176.

[8]Cheng Y，Qi W，Cai W.Dynamic properties of Elman and modified Elman neural network[A].2002 International Conference on Machine Learning and Cybernetics[C]，2002：637-640.

[9]Liu J，Wang G，Yu J.A Study of SMO buffeting elimination in Sensorless control of PMSM[A].IEEE 2010 8th WCICA[C]，2010：4948-4952.

[10]刘金坤.滑模变结构控制MATLAB仿真[M].北京：清华大学出版社，2006.