木材CT图像的三维重构
王在山,戚大伟
(东北林业大学 理学院,哈尔滨 150040)
随着计算机断层扫描(Computed Tomography)成像技术的不断发展,虚拟现实技术的应用领域范围在不断扩大,其中利用CT图像分析探索木材内部缺陷是近几年逐渐兴起的一项新技术。CT检测作为X射线无损检测的分支,是X射线的一种应用[1]。运用CT检测能够有效的防止传统X射线检测三维信息重叠和分辨率较低所造成的影响,加强了木材缺陷检测的质量,同时能够精确的获得木材内部缺陷特征及位置。利用虚实技术将二维图像在计算机上实现木材内部结构的三维重建,通过三维成像可获得多种方案的虚拟切割,选用最佳的加工方案进行加工,具有广泛的应用前景。木材CT图像边缘信息提取的精确性直接决定三维重构的结果。
多重分形(Multifractal)也称作复分形,常被用来表示只用一个来源于整体的分形维数所不能完整描述的奇异规律分布的形式,借助某一普函数来论述不同层次的分形体的生长特征,利用局部系统的特征来研究最终的整体特征[2]。提供在尺度产生变化时为引起不等范围的幂定律现象的模型和奇异结构的测度量化,主要应用于难以建立数学模型的无规则图像的信息进行处理[3-4]。
线性插值法是数学、计算机图形学等领域广泛使用的一种简单插值法。常用于已知函数f在两点的值的近似获得其它点数值的方法。在研究层间轮廓线性插值各种插值点对建立方法上,经过平行移动使它的终止轮廓的形心与起始轮廓的形心相重合[5]。运用直接搜索法确立初始值点对,构建其余插值点对,然后经过平行移动来还原插值点对的坐标值以及得到插值轮廓的顶点坐标。
伴随着三维重构技术在各个检测领域的迅速发展,应用在木材CT图像三维重建的软件越来越多,但是这些工作站的花费比较昂贵,致使其无法得到普及利用。而本文所选取的利用多充分性频谱技术与线性插值法相结合的方法能够快速、简单的实现CT图像的三维重建,花费大幅降低,而形成的图像也完整、清晰。
1 多重分形频谱技术与数据处理
1.1 多重分型频谱
HIder指数α是Haudorff频谱用来定义分形体各个小区域的分维,但是分形体具有很大数目的小区域,因此可得到由不同α构成的无穷序列谱f(α),f(α)即为奇异谱。
令HIder指数α的点集为Eα,fh(α)=dimh(Eα),dimh是多重分形的维,那么称fh(α)为Eα的多重分形频谱,所以Haudorff频谱可以准确地描述整体的Eα。
选择一个容量序列υn及参考测度μ[6],运算得出该图像的HIder指数的α(χ)以及Haudorff频谱fh(α(x)),再通过(α(χ),fh(α(x)))运用概率和几何的方法来逐个分类及处理图像的所有像素点。由此可得出,图像的整体性和局部的特征是判定一个像素点是否是边缘像素点的决定性因素。
1.2 多重分形频谱的选择
根据多重分形理论可知:具有较低规律性的点来源于粗糙区域,要找到一种区分轮廓线的方法,当某一点的HIder指数所对应的Haudorff频谱的数值f(α)=1时,那么可以确定该点在轮廓上;边缘上的点存在几何学和统计学特征。在某一个图像中随意的选定一个像素点,我们就可以由它得到的概率来判定这个点是否在边缘上。比如,当Haudorff频谱值f(α)=1时,就能得出所有的边缘点;当频谱值f(α)=1.5,就能得到由边缘点绘画成的不规则的线;当Haudorff频谱值趋近于2时,就能得到粗糙区域或光滑区域的具体信息[7]。
1.3 实验对象的选取
运用CT技术对木材的缺陷进行检测,相比于传统的无损检测技术,CT检测的优点:CT给出的被检测原木的断层扫描,用CT扫描木材得出的图像,可以清晰地得到缺陷的大小、形状以及所处木材内部的空间位置,不受其它因素的影响;传统的无损检测是将原木放在射线接收屏和放射源中间,将整个木材的信息投影到一个平面上得到图像,图像中的信息是重叠的,无法清晰的确定目标细节。
1.4 原木CT图像处理与分析
如图1所示为一幅原木CT断层扫描图像,图2~图5分别为使用Robert算子、Sobel算子、Log算子和Canny算子对图1通过边缘检测处理后得到的图像。图6~图7为使用多重分形进行边缘检测的结果。
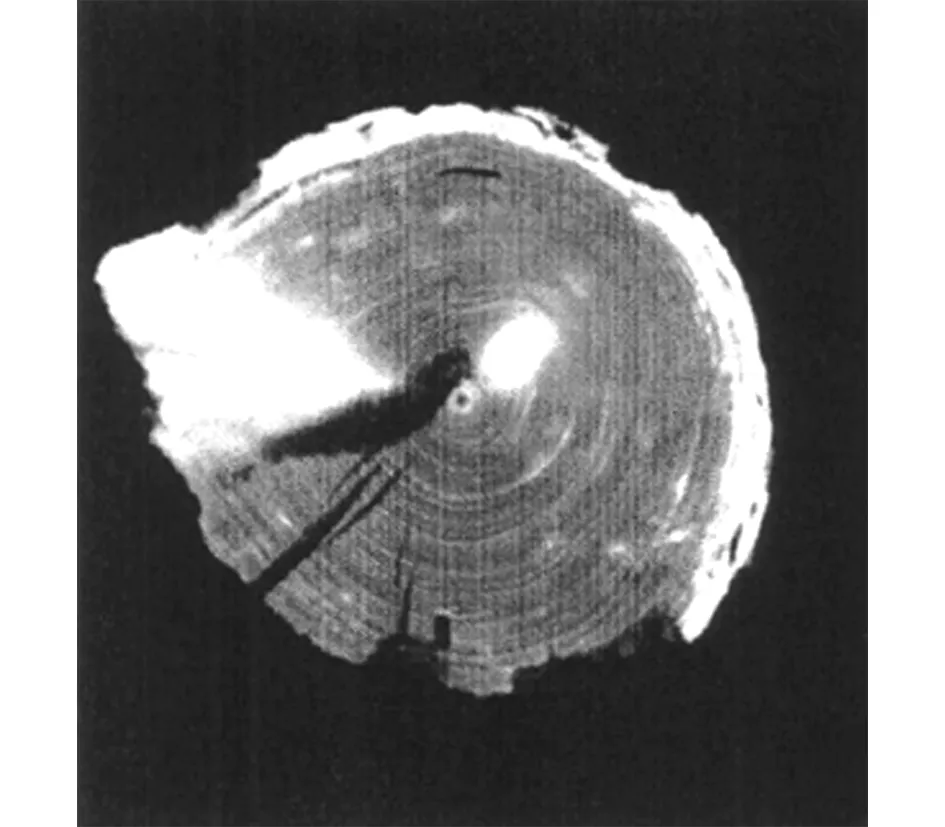
图1 木材CT断层扫描图像

图2 Robert算子处理的图
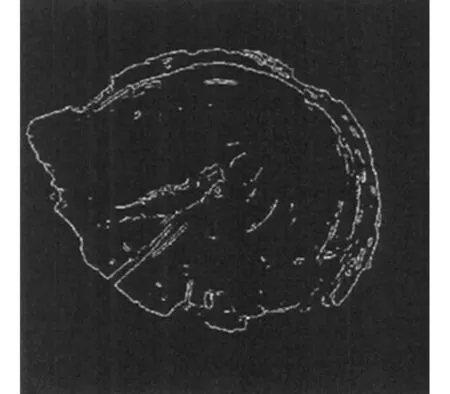
图3 Sobel 算子处理过的图像
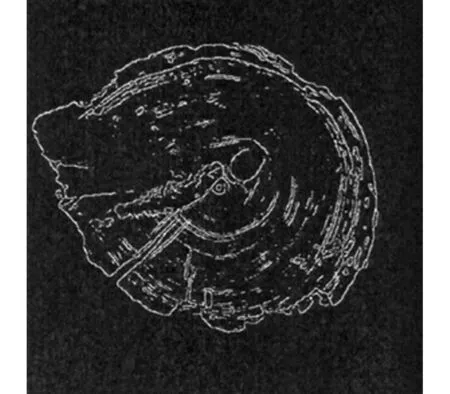
图4 Prewitt算子处理过的图像

图5 Canny算子处理过的图像

图6 频谱值1.0≤f(α)≤1.2处理过的图像
2 线性插值法及三维重建
2.1 线性插值法
如图7所示,将已知的两个轮廓分别定义为起始轮廓CS和终止轮廓CG,插值得到的轮廓称为差值轮廓或结果轮廓CT各种层间轮廓线性插值方法的基本原理:在已知的两个轮廓中确立一个插值点对,PS0与PG0,再运用差值平面Q截取PS0PG0的连线来获得插值点,则差值轮廓的顶点为获得的交点PT0,差值的轮廓就是由所有的交点组成的集合所确定的。
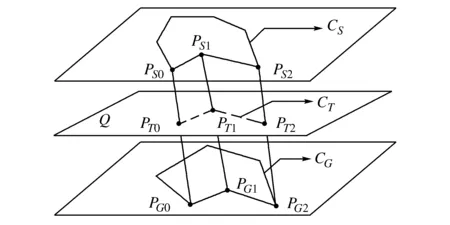
图7 线性插值原理
2.2 基于线性插值法的三维重建
CT扫描获得图像的厚度为8 mm,运用线性插值法对两相邻的图像进行差值,则断层图像的厚度变为4 mm,将所有图像进行差值得到的图像的数量是原先的两倍,这种方法能够将三维重建过程中产生的失真降低。
运用Haudorff频谱对木材CT图像进行边缘检测,提取出图像的轮廓,再对提取出的轮廓进行线性差值,然后对获得的所有轮廓进行逐一整合,从而得到三维的木材表面的轮廓,如图8所示。对获得的木材CT图像进行线性插值计算,将得到的图像再与原扫描图像按之前进行处理的顺序相结合,从而能够得到木材内部的三维重建,再与得到的三维表面轮廓相组合,即得到木材CT图像整体的三维重构,如图9所示为不同角度观察的整体投影图像。

图8 三维重建轮廓图像

图9 不同视角的三维重建观测投影图像
3 结 论
Haudorff频谱对木材的CT图像进行边缘检测,具有以下优点:高准确度和强局部性,能够保留更多的边缘细节,提取出的边缘清晰、完整,在保持图像的边缘细节上具有较好的效果。运用线性插值法对木材CT图像进行三维重建,该方法能够高效的完成三维重建,具有运算效率高以及能够直观、清晰的重建木材的三维轮廓的特点,可以精确的对木材内部各种缺陷的大小、形状、空间位置等做出判断,为木材的虚拟切割和合理利用木材提供了一种有效的方法。由本文可以得出,对木材CT图像进行三维重建的过程中,采用线性插值法结合多重分形频谱的方法是一种简单、有效的方法,提供了一种新的思路。
【参 考 文 献】
[1]于 雷,戚大伟.计算机断层扫描技术检测木材内部缺陷的研[J].森林工程,2006,22(5):13-15.
[2]张济忠.分形[M].北京:清华大学出版社,2004.
[3]Falconer K J.分形几何学中的技巧[M].曾文曲,王向阳,陆 夷,译.沈阳:东北大学出版社,1999.
[4]朴顺姬,戚大伟,金雪婧.多尺度分形特征在木材内部缺陷检测中的应用[J].森林工程,2012,28(5):56-59.
[5]王 巍,洪 军,王永银,等.基于断层图像的RP三维重构中层间轮廓线性插值算法[J].机械工程学报,2006,42(7):170-175.
[6]Véhel J L,Vojak R.Multifractal analysis of Choquet capacities:preliminary results [J].Adv.Appl.Math,1998,20(1):1-43.
[7]Canus C.Robust large deviation mutifractal spectrum estimation [J].Journal of Mathematics,1995,35:462-490.

