基于灰色逼近理想点高速公路安全设施评价

高 贺，周会聪

(东北林业大学 土木工程学院，哈尔滨 150040)

高速公路交通安全设施，在保证驾驶安全性、车辆高速连续行驶创造良好的驾驶环境等起着重要的作用[1]，因此，对高速公路安全设施系统开展客观评价是十分必要的。然而，在实际的指标评价体系中，指标变量错综复杂，指标数据的不完全性和不确定性呈一定程度的灰色关系。在以往的评价过程采取的评价方法中，或者过于简单，信息丢失太多，使评价结果难以令人信服；或者过于复杂，可操作性不强，缺乏实用价值。基于以上情况，本文引入灰色关联分析理论指导，借助于逼近理想点法的思想，构建评价指标体系，建立更加客观合理的高速公路安全设施评价模型。

1 评价指标体系建立

1.1 高速公路安全设施评价指标筛选

目前，国内外对于高速公路安全设施系统评价并未形成一套完整的、科学的和完善的评价体系。在以往的指标体系建立中，高速公路安全设施指标体系大小不一，而大量相应指标内部之间都有较强的关联性，并且在一定程度上定性指标在指标数据获取的可靠度难以保证。

为了更加客观科学地评价高速公路安全设施系统，需要建立一套科学、完整及能够从全方位、多角度反映出高速公路安全设施实际运行水平的指标体系。为此，在选取指标时，遵照系统性、有效性、可比性及可操作性的原则，筛选出既能反映高速公路安全设施的主要方面，同时又能从现有的统计资料中获取数据的指标构建高速公路安全设施系统的指标体系。

通过查阅大量的参考资料及综合专家意见[2-3]，建立的评价指标体系由7大类22项基本指标构成，与以往的指标体系相比更加全面综合地考虑了经济、生态、社会等因素对高速公路安全设施影响较大的指标，而并非仅仅从安全的角度出发。该指标体系可以更好地反映高速公路安全设施实际效果的基本内涵。指标体系见表1。

表1 高速公路安全设施评价指标体系

1.2 评价指标标准化

将建立的高速公路安全设施评价指标体系细分为效益型指标(指标值越大越好)、成本型指标(指标值越小越好)和固定型指标(指标值越接近某一定值越好)，针对不同类型的指标采取对应的方法分类进行归一化处理，公式如下：[4-5]

(1)

(2)

(3)

其中xj为评价指标的最佳值。

2 灰色关联逼近理想点法

2.1 基础理论

高速公路安全设施评价体系是一个涉及多目标、多层次、多因素的评价过程。由于在高速公路安全设施评价体系中，部分指标所获取的数据无法从统计资料中获得，因此该系统具有“灰色”的特征，即信息不完全性和不确定性，运用灰色系统理论中的灰色关联分析评价该系统是合理可行的。灰色关联分析是挖掘数据内部规律的有效方法，能够定量描述或比较系统之间的接近程度，根据接近程度来计算关联度[6]。

然而，以往的灰色关联算法通常是以理想最优的方案作为参考序列，计算得出的结果只能反映与理想最优方案的关联度，并使得评价结果偏优，与现实情况不符。因此，本文引入逼近理想解排序法，将欧氏距离和灰色关联度有机结合，即灰色关联逼近理想点法，构造了一种新的相对贴近度，以实现对方案的评价及排序。新贴近度同时反映了方案与理想方案和负理想方案之间的位置关系和数据曲线的相似性差异，含义更加明确。

2.2 基于灰色关联逼近理想点法的评价步骤

综上所述，进行多指标评价时，基于灰色关联逼近理想点法的评价过程可归纳如下[7-9]。

(1)收集决策数据，建立评价矩阵；假设对m个评价指标进行评价，包含n个样本，则相对应的评价指标值为：rij(i=1,2,…,m,j=1,2,…,n)。所对应的指标矩阵为：R=(rij)m×n

(4)

(2)对评价指标进行分类，按照不同类型指标，对评价矩阵进行标准化处理，得到标准化矩阵：Y=(yij)m×n

(5)

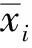
(6)

(7)

式中：xji为第j个被评价对象在第i项指标上的取值。各指标的变异系数vi为：

(8)

对vi作归一化处理，便可得到各指标的权数：

(9)

最终矩阵为：

W=(w1,w2,…,wm)T。

(10)

(4)计算灰色关系数，其中：

(11)

其中：

▷(min)=minjmink|X0(k)-Xi(k)|▷(max)=maximaxk|X0(k)-Xi(k)|▷ok(t)=|X0(k)-Xi(k)|。

式中：εi(k)为比较数列Xi与参考数列X0在第k个评价指标上的相对差值；ρ为分辨系数，人为引入这个系数是为了提高关联系数之间的差异显著性或敏感性，通常取0.5，取值范围为0<ρ<1。

(5)建立加权灰色关联系数矩阵。

R=(Rij)m×n=(Wjεij)m×n。

(12)

(6)确定灰色关联理想解和灰色关联负理想解。

(13)

(14)

(7)计算各待评方案到灰色关联理想解与灰色关联负理想解的欧式空间距离。

。

(15)

其中：i=1,2,…,m

。

(16)

(8)计算各候选方案与理想方案的贴近度，根据c的值从大到小排序，作为方案优选的依据。

(17)

3 实例分析

选取黑龙江省内5条高速公路作为样本数据进行分析与评价，数据来源为现场调研及相关部门提供。通过已获取数据，运用灰色逼近理想点法综合评价模型对高速公路安全设施系统开展评价。

3.1 建立评价矩阵及指标标准化处理

首先，将所收集数据进行整理，根据公式(4)建立评价矩阵。将评价指标体系中的基本指标按照不同类型进行分类。指标归类后分别按照公式(1)、公式(2)、公式(3)对三种不同类型的指标进行标准化处理，得到如下标准化矩阵。

其中效益型指标包括：c3,c4,c5,c10,c14,c15,c17,c19,c21,c22；成本型指标包括：c1,c2,c6,c7,c9,c12,c13,c20；固定型指标包括：c8,c11,c16。

Y=[yij]m×n

0.5450.818100.3480.8390.804100.3930.4120.23500.74510.2250.145010.7910.55300.6590.3830.9640.357010.78610.7140.64300.85700.0780.2160.745100.9230.3930.143100.4690.2810.781100.3750.1880.7510.37900.6210.89710.66711010.2610.54300.93510.6250.90600.87510.57100.28610.8570.6670.60400.917110.57600.7270.93910.4750.62700.27110.5930.49200.77900.22810.9290.33310.6280.2560.3590

3.2 指标权重确定

在权重值设定时，采用客观赋权法中的变异系数法进行权重确定，按照公式(6)～(10)计算，按指标顺序相应排列得到的权重结果如下：

3.3 确定加权灰色关联系数矩阵

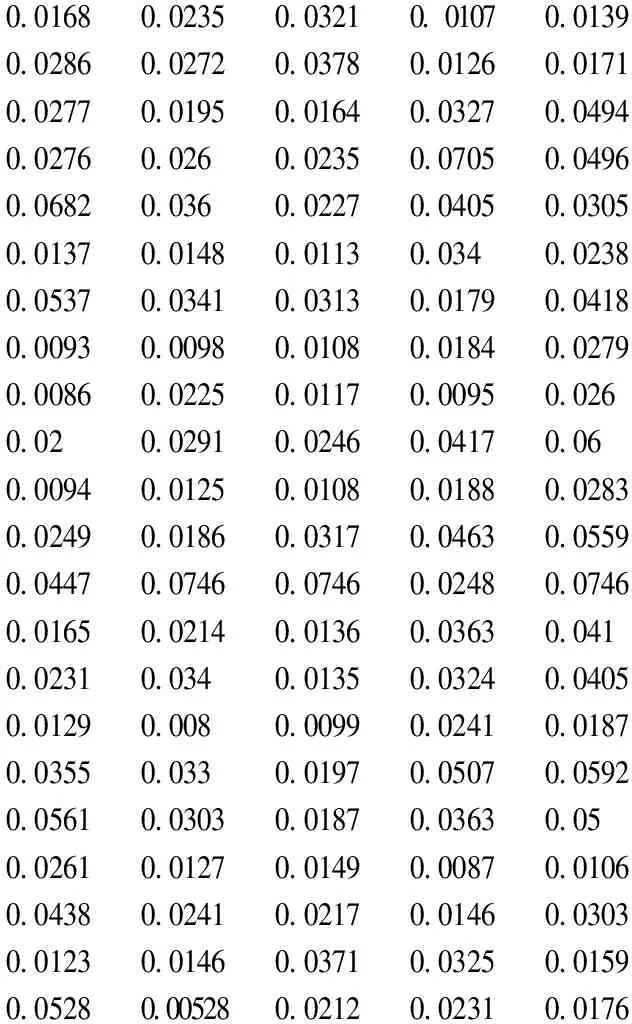
按照公式(11)计算灰色关联系数，其中分辨系数取0.5，并按照公式(12)计算求得灰色关联加权矩阵如下：

R=(Rij)m×n

0.01680.02350.03210. 01070.01390.02860.02720.03780.01260.01710.02770.01950.01640.03270.04940.02760.0260.02350.07050.04960.06820.0360.02270.04050.03050.01370.01480.01130.0340.02380.05370.03410.03130.01790.04180.00930.00980.01080.01840.02790.00860.02250.01170.00950.0260.020.02910.02460.04170.060.00940.01250.01080.01880.02830.02490.01860.03170.04630.05590.04470.07460.07460.02480.07460.01650.02140.01360.03630.0410.02310.0340.01350.03240.04050.01290.0080.00990.02410.01870.03550.0330.01970.05070.05920.05610.03030.01870.03630.050.02610.01270.01490.00870.01060.04380.02410.02170.01460.03030.01230.01460.03710.03250.01590.05280.005280.02120.02310.0176

3.4 确定灰色关联理想解与负理想解

按照公式(13)、(14)确定灰色关联理想解V+与灰色关联负理想解V-：

3.5 计算欧式空间距离

根据公式(15)、(16)计算各待评价方案到灰色关联理想解与灰色关联负理想解的欧式空间距离：

D+=[0.0965,0.1066,0.122,0.0965,0.0715]。

D-=[0.0935,0.0684,0.0685,0.087,0.116]。

3.6 计算相对贴近度

根据公式(17)计算各待评方案指标值与灰色关联理想解的相对贴近度：

c=[0.492，0.391，0.359，0.474，0.550]。

得出高速公路安全设施综合排序：

5>1>4>2>3。

3.7 改变分辨系数后的综合排序

考虑到灰色关联系数的计算中，分辨系数的选择并没有一个明确合理的标准，通常取值为0.5，取值范围为0<ρ<1。现将分辨系数取不同值，验证分辨系数改变下对评价结果的影响。结果见表2和表3。

表2 不同分辨系数下贴近度的结果

表3 不同分辨系数下高速公路安全设施实际效果排序

由表2和3分析可知，分辨系数越大，与理想方案的贴近度越强。并始终没有影响最终高速公路安全设施的优劣排序，进一步说明了模型评价的合理性。同时，在今后的高速公路相关建设方案选择时，可以参照高速公路5作为标准。

3.8 结果分析

通过排序结果可知，高速公路5安全设施实际效果最好。经分析该条高速公路所有设计要求参照最新规范，在设计过程中兼顾行车安全以及以人为本的中心思想，全面系统地考虑了高速公路安全设施对经济、生态、社会等因素的影响，并采用了较新的设计理念，故该条高速公路安全设施实际效果最好。该评价结果表明：高速公路综合排序结果与现实情况一致，从而科学有效的验证了模型的合理性。

4 结 论

本文从系统性、有效性、可比性及可操作性等多角度出发，建立了高速公路安全设施评价指标体系，应用灰色逼近理想点法相关理论，结合实例得出如下结论：

(1)构建了基于7个一级指标、22个二级指标的高速公路安全设施评价指标体系，能够全面合理的涵盖所需评价的内容，适用性更强。

(2)通过综合灰色关联分析与逼近理想点法各自的优点，提出了一种更加科学合理的多指标评价方法。结果表明，应用灰色逼近理想点法进行高速公路安全设施系统评价是合理可行的。

(3)结合黑龙江省5条高速公路验证分析，通过研究不同分辨系数下贴近度的结果可知，分辨系数越大，贴近度越强。

(4)分辨系数的改变并未影响最优排序的结果，高速公路5的安全设施实际效果最好。结果表明，在应用灰色逼近理想点法模型时，应该结合分辨系数进行综合分析，才能做出最正确的评价。该评价模型可以客观有效地评价高速公路服务现状。

【参 考 文 献】

[1]李富勇.高速公路交通安全设施系统评价研究[D].西安：长安大学，2006.

[2]王建军，刘乙橙，吴宜淞.高速公路交通安全设施系统评价指标及评价方法研究[J].交通运输系统工程与信息，2007(4)：6-70.

[3]陈毕伍，廖晓峰.公路交通可持续发展评价指标体系研究[J].中国公路学报，2009，22(5)：111-117.

[4]曹永军.高速公路交通工程设施系统分析及评价研究[D].西安：长安大学，2006.

[5]艾正海.关于多目标决策问题的理想点法研究[D].成都：西南交通大学，2007.

[6]王冬霞，灰色系统理论用于水电工程项目风险管理的研究[D].哈尔滨：哈尔滨工业大学.2006.

[7]张 毅，丘海礼，朱 江.改进逼近理想解排序法的供应商评价和优选[J].河南科技大学学报(自然科学版)，2013，34(3)：100-104.

[8]马超群，王玉萍，陈宽民，等，基于灰色加权关联度的城市轨道线网方案评价[J].长安大学学报(自然科学版)，2007，27(3)：84-87.

[9]张静静.基于逼近理想解法的第三方物流服务商选择研究[D].西安：长安大学，2010.

[10]郭延永，刘 攀，吴 瑶，等.基于属性识别的高速公路交通安全设施系统评价[J].东南大学学报(自然科学版)，2013，43(6)：1305-1311.