基于价格和销售努力补贴的库存模型

葛安华，苑文雅，白晓宇

(东北林业大学 工程技术学院，哈尔滨 150040)

在经济快速发展竞争激烈的环境下，经典库存控制EOQ模型不能完全适用于现在的市场需要。对市场的调查研究可以发现销售商所确定的销售价格和销售努力投入对市场的需求具有决定性的影响，同时越来越多的销售商意识到只有与供应商有效合作才能达到双赢。Kunreuther和Richard[1]第一次从定量的角度建立需求受价格影响的最优订购批量以及最优销售价格的数学模型；Baker W[2]和Huang Z[3]以广告作为促销手段建立供应商和销售商之间的供货模型；周永务[4]、汪峻萍[5]在考虑价格与广告投入费用的前提下，建立了商品的最优广告投入与订货策略的随机模型；胡本勇[6]、李清艳[7]在研究收益共享和销售努力成本共担的供应链模型中，分析了销售努力共担对供应链的协调的影响。

虽然许多研究者针对不同的合作问题建立了需求与价格、销售努力等相关的分析模型，但是在批量折扣前提下，把销售价格、销售努力以及供应商共担的销售努力补贴同时引入进行决策的却很少。本文以价格和销售努力决定的需求函数为前提，引入供应商提供的销售努力补贴，建立销售商最优的定价订货模型，以达到利润最大化。最后通过数值实例对模型进行验证。

1 销售商依赖价格和销售努力补贴的库存模型

1.1 参数意义与模型假设

(1)参数意义见表1。

(2)模型假定：①假设系统在无限周期水平上运行并且不允许缺货，补充缺货瞬时完成；②边际收入d(pD)/dD=p+D/D′是关于p的增函数[8]，对于任意的p，都存在2-(DD″/D′2)>0。

表1 参数意义

1.2 模型建立

最优库存控制的决策问题可以转化为存在批量折扣的情况下，如何确定最优的销售价格、订购量以及最优销售努力投入[9]，从而使销售商在一个周期内的平均总利润达到最大。

1.2.1 需求函数的确定

销售努力投入越多，就有越多的顾客了解其经销商品和经营场所的有关情况，因而对其经销商品的需求量就越大。但不能无限制增长，其递增效用会逐渐减弱，最终趋于零。在保证销售价格不变的前提下，受销售努力影响的增加的需求量为D(I)=αIβ[7]，此函数应用较为广泛更符合实际。α为促销投资系数，β为投资的弹性，由于边际效用是逐渐递减的，所以0<β<1 。

综合考虑需求受价格和销售努力的影响，则需求函数为D=f(p，I)=a-bq+αIβ(以下简称为D)。

1.2.2 供应商的批量折扣

在实际中，销售商单位产品的购进价是与其订购批量紧密联系的，订购批量越大，订购进价相应的减少，即批量折扣。考虑到简化模型，本文采用符合实际且运用广泛的全单位量折扣[4]，模型如下：

式中：c0>c1>…>cm。

1.2.3 模型的建立

一个周期内销售商所获得的平均总利润，与销售收益R、购买费用Cp、库存费用Ch、订购费用C0以及销售商努力投入CI有关，是I、p、Q的函数，记为G(I，p，Q)(以下简称为G)。其中，R是指企业在一定时期内销售产品的货币总收入，R=pD。Cp是指支付给供应商的所购物品的费用，Cp=cD。Ch是指货物入库到出库过程中用于物品保管的所有费用，可以简单地用单位产品在单位时间内库存持有成本占销售商单位购买成本的百分比来计算，Ch=Qhc/2。C0是指销售部门每订购一次货物所发生的费用，该项费用只与订购的次数有关，C0=AD/Q。CI是指在一个销售周期内，销售商为了促进商品销售所做的投入，本文考虑供应商向销售商提供的销售努力补贴，则销售商实际所做的销售努力投入为CI=λID/Q。

(1)

根据一阶最优性条件可得，最优的p*需满足下式：

(2)

再求G在p=p*的二阶偏导得，

同理最优的I*需满足下式，

(3)

再求G在I=I*的二阶偏导得：

(4)

将函数D(I*，p)=a-bp+α(I*)β带入公式(4)化简得：

因此，对于确定的订购批量Q，带入公式(2)和(3)求得p*和I*实际上是关于Q的函数，即p*=p*(Q)，I*=I*(Q)。将p*和I*带入式(1)，那么销售商的平均总利润可以表示为只关于Q的一元函数，不妨记为G(p*，I*，Q)=G1(Q)。然后，求最优订购批量Q*使G1(Q)取得最大值。

根据一阶最优性条件可得，最优的Q*需满足下式：

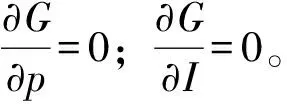
(5)

把函数D(I，p)带入(2)、(3)、(5)整理并化简得方程组：

(6)

2 实 例

以哈尔滨市大型超市家乐福所销售的维达四层薄荷手纸帕为例。经过调查发现家乐福销售的同类产品大约有10余种，每种又有不同的系列，价位在3～11元/条不等，同类产品之间可替代性强，需求价格弹性较大。根据以往的销售记录，利用多元回归分析的方法预测需求函数为D(p，I)=3600-400p+500I0.2。每次订购该商品需要的固定订购费用为A=200元，单位产品在单位时间内平均库存持有成本占零售商单位购买成本的百分比为h=40%，供应商对销售商所做的销售努力补贴率，则λ=1-s=0.8。供应商提供的全单位数量折扣如下：

考虑销售努力投入时，将所有已知的参数带入公式(6)中，利用matlab软件可算出不同订购价格下销售商的最优订购量、销售价格及销售努力投入见表2。

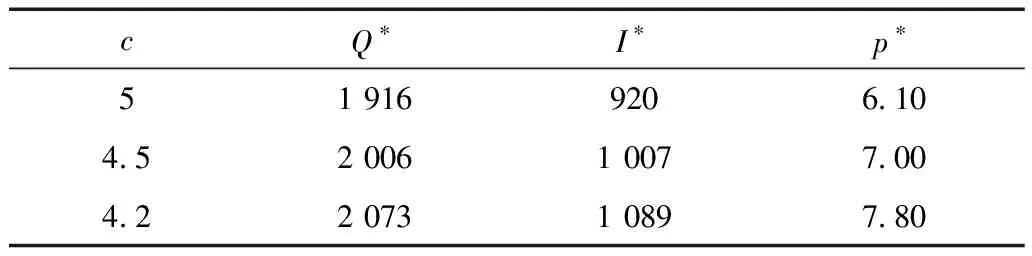
表2 计算结果

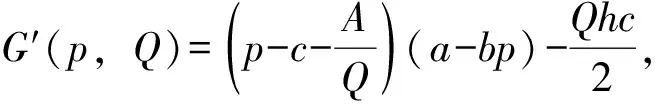
可以看出，在给定的数值条件下，考虑销售努力和不考虑时最优销售价格相差不大，但是大大提高了订购批量，从而验证销售努力促进商品的销售，提高销售商的平均总利润。

3 结 论

在批量折扣情况下，建立了由一个供应商和一个销售商组成的销售努力共担的库存控制模型。运用线性需求函数，并引入销售努力以及销售努力补贴更加贴近现实的市场运营形式。不同于传统的库存控制只确定最优订购批量，还确定了最优销售价格和销售努力水平。并通过实例进行验证，最后证明销售商平均总利润明显增加。

【参 考 文 献】

[1] Kunreuther H，Richard J F.Optimal pricing and inventory decisions for non-seasonalitems[J].Ecnometrica，1971，39(1)：173-175.

[2] Baker W，Marn M，Zawada C.Price smarter on the net[J].Harvard Business Review 2001，79(2)：122-127.[3] Huang Z，Li S X.Co-op advertising models in a manufacturer retailer supply chain：A game theory approach[J].European Journal of Operational Research，2001，135(3)：52-544.

[4] 周永务.库存控制理论与方法[M].上海：科学出版社，2009.

[5] 汪峻萍，周永务，杨剑波.需求依赖广告费用和销售价格的 newsboy 型产品库存模型[J].控制与决策，2010，25(1)：89-92.

[6] 胡本勇，王性玉.考虑努力因素的供应链收益共享演化契约[J].管理工程学报，2010，24(2)：135-138.

[7] 李清艳.需求依赖销售努力和销售价格的库存模型[D].合肥：合肥工业大学，2011.

[8] 克里斯托弗.R托马斯.管理经济学第九版[M].北京：机械工业出版社，2009.

[9] 杨英姿，杨慧敏，王 雨.基于RFID技术的现代仓储管理优化设计[J].森林工程，2013，29(3)：115-117.

[10] 高鸿业.西方经济学[M].北京：中国人民大学出版社，2007.