一种改进的基于差别矩阵的求核属性算法

陆 光，李 想

(东北林业大学 信息与计算机工程学院，哈尔滨 150040)

粗糙集是一个强大的数据分析工具，能表达和处理不完备信息，目前已被广泛应用于数据挖掘和智能决策等各个领域[1]，其表现为能提高对不完整数据进行分析和学习的能力。求核、属性约简、规则提取都是粗糙集理论中非常重要的研究课题。众所周知，通过属性约简删除冗余属性，可以提高系统潜在知识的清晰度。由文献[2-3]可知，最常见的约简模型有：基于正域的属性约简模型[4]，基于条件属性熵的属性约简模型[5]，基于skowron的差别矩阵的属性约简模型[6]，基于分配的属性约简模型[7]，以及基于近似的属性约简模型[8]等。对于大多数约简模型，其算法一般要先求出其核，然后再根据核，通过启发式知识加入其它属性，扩展到最小约简。基于skowron的差别矩阵是一种非常经典的的求核方法，很多学者通过改进其方法，使其得到的结果最优，其中，Hu提出将改进的skowron的差别矩阵方法应用在决策表的属性约简中，得到基于差别矩阵的Hu属性约简[6]。现有研究结果表明基于正区域的属性约简模型的核，基于Skowron差别矩阵的属性约简的核和基于信息熵的求核模型得到的结果是不完全等价的[3，9]，因此，改进Hu差别矩阵方法是当前研究的热点[10]，张振林等提出了改进的差别矩阵方法，大大减少了数据存储空间。本文基于张振林等的改进的差别矩阵方法基础上提出分决策属性“D集”的求核方法。

1 粗糙集理论基本知识

有关粗糙集的相关基础知识请参考文献[4，11]，不同书籍或文献对粗糙集的概念描述有所不同，如粗糙集方法是一种能有效地分析和处理不精确、不一致、不完整等各种不确定性信息的数据分析工具；粗糙集的研究对象是由一个多值属性(特征、症状、特性等)集合描述的一个对象(观察、病例等)集合[12]；粗糙集理论的观点是，“知识(人的智能)就是一种对对象进行分类的能力”[13]。粗糙集理论对事物的表述不需要任何假设的先验知识，只依赖于给定的知识表达系统。知识约简在智能信息或数据的处理中占有十分重要的地位，也是粗糙集理论的核心内容之一。知识表达系统中有一种叫决策系统，也称决策表，即含有决策属性的知识表达系统。

定义1[13]设在决策表S=(U，C，D，V，f)中，记U={x1,x2,…,xn}，为对象的非空有限集合，称为论域；C={α|α∈C}称为条件属性集，每个αj∈C(1≤∈j≤m)称为C的一个简单属性；D={d|d∈D}称为决策属性集，且C∩D=Ø，C=Ø，D=Ø；V=UVα(∀α∈C∪D)是信息函数f的值域，而Vα表示值域；f={fα：U→Vα,α∈C∪D}表示决策表的信息函数，fα为属性α的信息函数。

定义2[13]决策表S=(U,C,D,V,f)，∀α∈C∪和∀x∈U，定义dx：C∪D→V,α|→dx(α)=α(x)为决策表的决策函数。

dx|C表示决策函数dx被限制为只能在条件属性集C上取值，称为dx的条件；

dx|D表示决策函数dx被限制为只能在决策属性集D上取值，称为dx的决策；

∀y∈U，且y≠x，如果有dx|C=dy|C⟹dx|D=dy|D成立，则称决策dx是相容的，也称一致的，否则为不相容或不一致的；若∀x∈U,dx是相容的，则称决策表是相容的。相容决策表中有一个颇为重要的性质，即POSC(D)=U。

核是粗糙集理论中所有属性约简的交集，意味着核包含在知识的每一个约简中，是约简的最基础部分。基于相对正域的一般求核方法，思想是求出决策属性在整个条件属性集上的正域，记为POSC(D)，再去掉一个条件属性在整个条件属性集上的正域，记为POSC(D)，若POSC(D)≠POSC(D)，则称去掉的这个属性为核属性。定义如下：

定义3[11]在决策表S=(U,C,D,V,f)中，若∀B⊆C,POSB(D)=POSC(D)；∀b∈B均有POSB-|b|(D)≠POSC(D)，则称B是C相对于D的基于正区域的属性约简，记其所有的属性约简为PREDD(C)。称Core(C)=∩B⊆PREDD(C)(B)，为正区域属性约简模型的核，简称为正区域的核。

基于正域的求核方法，有时不会那么尽如人意，虽然会得到核集，但是不排除得到的核集就是属性全集，如果采用深度或者宽度优先等策略可以得到所有可能的约简结果，但是文献[14]中证明了穷尽的搜索花费的时间和空间代价是非常高的，是一个NP-hard问题。

差别矩阵的概念由波兰华沙大学数学家Skowron于1992年提出，方法是通过矩阵求得约简，再由所有的约简交集得到核属性[15]。

定义4设S=(U,C,D,V,f)是一个决策表，其中，论域是对象的一个非空有限集合U={x1,x2,…,xn}，|U|=n，则定义：

为决策表的差别矩阵，其中，i,j=1,2,…,n。

Ø为如果论域中两个对象的决策值不同，但属性值全部相同，说明两个对象所对应的决策是不相容的；

“-”为如果论域中两个对象的决策值相同，则没有必要考虑它们存在的差异；

在一个相容决策表中，决策表的相对D核等于该差别矩阵中所有单个属性组成的集合。差别矩阵会占用很大的存储空间，逻辑运算量很大。

HU对Skowron分辨矩阵进行改进，定义如下：

定义5[6]在决策表S=(U，C，D，V，f)中，设M=(mij)是HU的差别矩阵，∀B⊆C，若B满足：

(1)∀Ø≠mij∈M，有B∩mij≠Ø。

(2)∀b∈B,B-(b)不满足(1)，则称B是C相对于D的基

于HU的差别矩阵的属性约简.记其所有的属性约简为PREDD(C).称Core(C)=∩B⊆PREDD(C)(B)，为改进的基于skowron的差别矩阵属性约简的核。

叶东毅，杨明，孙志挥等，对Hu的方法进行纠正[16-17]，其中，杨明教授在文献中提出了一种核属性判定定理，张振林等学者基于此提出了一个新的简洁的核属性判定定理，以此为依据，提出了新的改进的差别矩阵及求核方法[18]，定义如下：

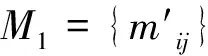
张振林等改进的差别矩阵算法中，省去了一些不必要的元素，减少了矩阵中非空元素的个数，减少了计算代价，降低了差别矩阵的复杂度。

2 改进的求核方法

上述求核方法中，基于相对正域的一般求核方法，其缺点是有时得不到单个的核属性，即使得到的是核集，也有可能是属性全集；Skowron提出的基于差别矩阵的求核方法，由于把所有属性相交的结果均存储，所以会占用较大的存储空间，并且对所有项进行计算，其计算量很大；HU对Skowron分辨矩阵改进的算法中，有时会有得不到核属性的情况出现；张改进的差别矩阵求核算法，由于省略了部分元素的计算，矩阵的规模缩减了很多，减少了存储空间占用，降低了差别矩阵的复杂度，但是在某些不相容决策表中，差别矩阵会存在两种情况：差别矩阵中并非存在单个属性，此时，得不到核属性；可能存在单个属性，但所有单个属性的并集为整个属性集，此时和基于正域的求核属性可能得到的结果一样，差别矩阵并未起到求核的作用。张的方法，差别矩阵中行和列的确定是比较模糊的，当决策属性有两种取值时，能轻松的得到行列的数据，而有些时候，决策属性值并非两种，此时，差别矩阵是不好确定的。基于此，本文提出了一种分级策略的求核属性方法，即根据决策属性的值提出分级策略，构成分级差别矩阵，通过本文方法，弥补了其他求核方法中得不到核属性的缺点，同时，通过决策值的分级策略，得到的分级矩阵，有效压缩差别矩阵中的空值元素，能减少存储空间。算法描述如下：

输入：一个决策系统S=(U，C，D，V，f)。

输出：属性核CORE。

Step1：判断数据是否为适合操作的数据形式，如果不是，则概化系统数据，即用相应的数字代替，并令CORE=Ø。

Step2：求U/C={X1,X2,…,Xn}和U/D={Y1,Y2,…,Ym,},POSC(D).如果POSC(D)=U，转到Step4；否则转到Step3。

Step3：α∈C,β∈C，如果α(xi)=β(xi)，则可以去掉α或者β,此时U=U-1,令U1=POSC(D)，U2=U/U1，构建差别矩阵M1，其中行由U1构成，列由U2构成：形成如下形式的矩阵：

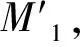
如果差别矩阵中存在单个属性，且所有单个属性的并集并非属性全集，则为核，转到Step5.

Step5：CORE={α}，算法结束。

3 实例分析

下面以一个不相容的交易决策表表1为例，对该算法进行解释说明。

决策信息表S=(U,C,D,V,f)，其中，U={{1}，{2}，{3}，{4}，{5},{6},{7},{8},{9}}c={a,b,c,d},D={e},Va={0,1,2},Vb={0,1,2,3},Vc={0,1,2},Vd={0,1,2,3}

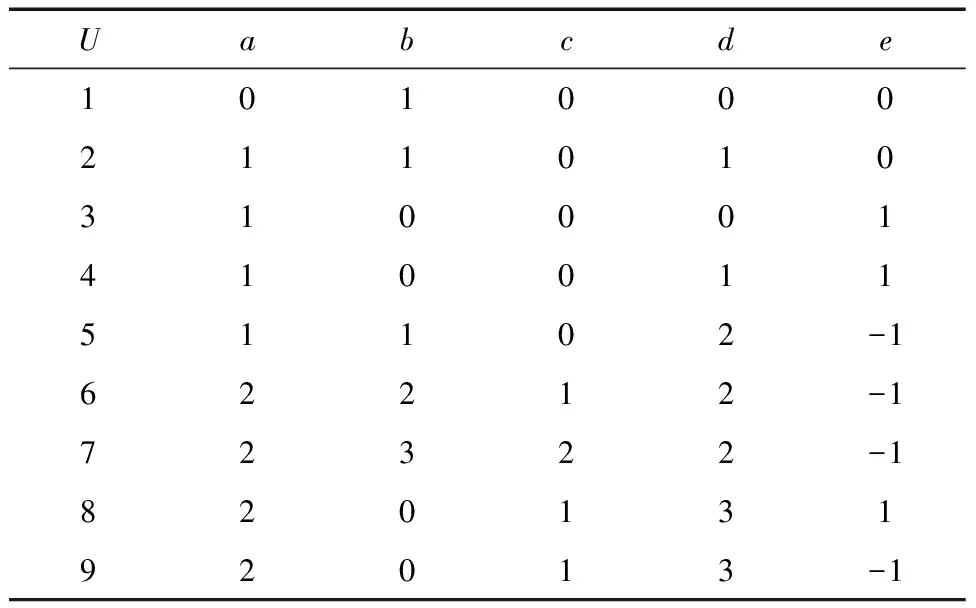
表1 决策信息表

(1)基于正域的求核方法：

U/C={{1}，{2}，{3}，{4}，{5}，{6}，{7}，{8，9}}

U/D={{1，2}，{3，4，8}，{5，6，7，9}

U/(C/{a})={{1}，{2}，{3}，{4}，{5}，{6}，{7}，{8，9}；

U/(C/{b})={{1},{2,4},{3},{5},{6},{7},{8,9}}；

U/(C/{c})={{1},{2},{3},{4},{5},{6},{7},{8,9}}；

U/(C/{d})={{1},{2},{3,4},{5},{6},{7},{8,9}}；

POSC(D)={{1},{2},{3},{4},{5},{6},{7}}

POSC/(a)(D)={{1},{2},{3},{4},{5},{6},{7}}

POSC/(b)(D)={{1},{3},{5},{6},{7}}

POSC/(c)(D)={{1},{2},{3},{4},{5},{6},{7}}

POSC/(d)(D)={{1},{2},{3},{4},{5},{6},{7}}

由上可知，POSC/(b)(D)≠POSC(D)，所以，核属性为{b}。

(2)张振林等提出的改进的求核算法如下：

由上述可知，POSC(D)={{1},{2},{3},{4},{5},{6},{7}}≠U，此时，U1={{1},{2},{3},{4},{5},{6},{7}}，U2=U/U1={{8,9}}，得到差别矩阵见表2。

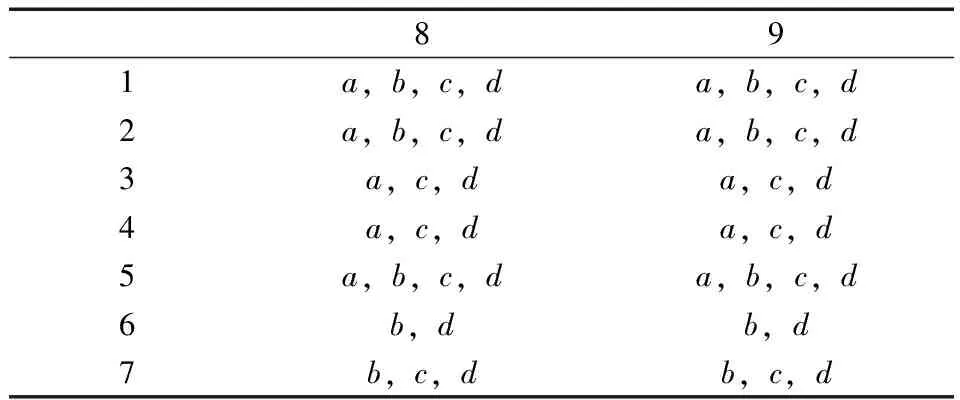
表2 差别矩阵表

表3 约简差别矩阵

上述矩阵中不存在单个属性，所以得不到核属性，并且，很容易看出，由于{8,9}∈U/C，所以，差别矩阵中，得到的两列数据是重复的，此时，会占用一定的存储空间，同时增加了计算量。

(3)本文改进的基于差别矩阵的分级策略求核算法处理如下：

Step1：由表1可知，决策信息表为适合挖掘的形式，不用再概化。

Step2：根据(1)中描述，POSC(D)≠U，则转到Step3。

Step3：由计算可知{8,9}∈U/C，则可以得到差别矩阵见表3，得不到单个的属性，即得不到核值，所以转Step4。

Step4：决策属性分级[D]i，此例中i=1,2,3，[D]1={1,2}，[D]2={3,4,8}，[D]3={5，6，7，9}，此时U也得到了分级，U1={1，2}，U2={3，4，8}，U3={5，6，7，9}，差别矩阵见表4。

表4 分级矩阵(1)

表4 分级矩阵(2)

由于决策属性取值分级为3，则可以形成如上的两个矩阵，两矩阵之间并不存在交叉重复的情况，从分级矩阵(1)中可看出，单个属性b,d，则核集CORE={b,d}，上述三种方法中，基于正域的核提取，本例中顺利得到核{b}；张振林等的方法，可以处理不相容决策表，但是构建的差别矩阵，没有对所有对象进行两两对比，可能会遗漏信息，同时差别矩阵的形成的数据可能是冗余的，如上述情况所示，当两个对象对应的所有取值都是一样时，既占用数据存储空间，又降低算法的运行效率和时间代价，也会有得不到单个属性的时候；本文提出的方法，不仅可以处理相容决策表，也能处理不一致决策表，避免了差别矩阵中出现冗余的数据。

4 实验分析

选择数据库中的6个数据集进行实验，实验数据为林农对林业保险的需求影响因素，其中条件属性包括林业生产损失程度、林木种植的最大风险类型、是否考虑用保险来分担风险、林农对风险的感知程度等，决策属性为林农是否愿意参加林业保险。具体信息见表5。计算机硬件配置Intel(R)Core(TM)i3 CPU M330 2.13GHz，内存2GB，开发平台为Myeclipse，用java语言实验本文的算法。

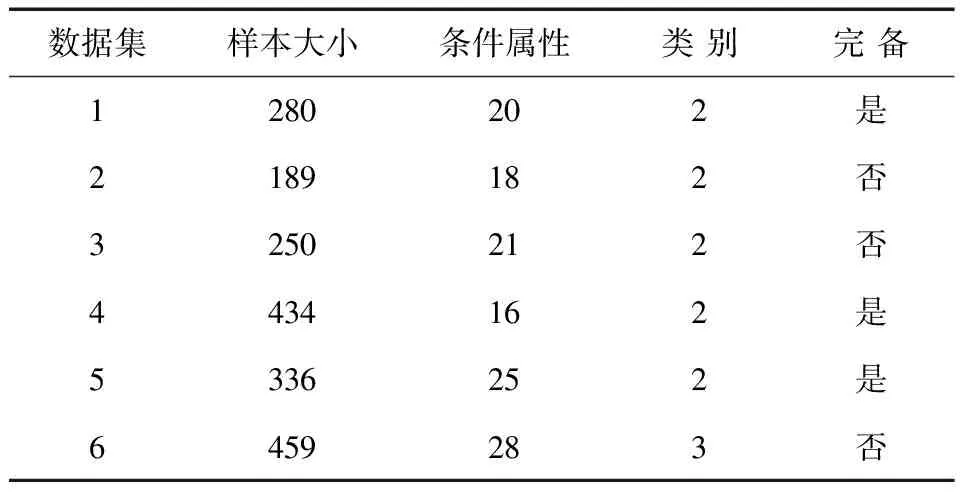
表5 数据集信息表

求核属性的结果见表6。

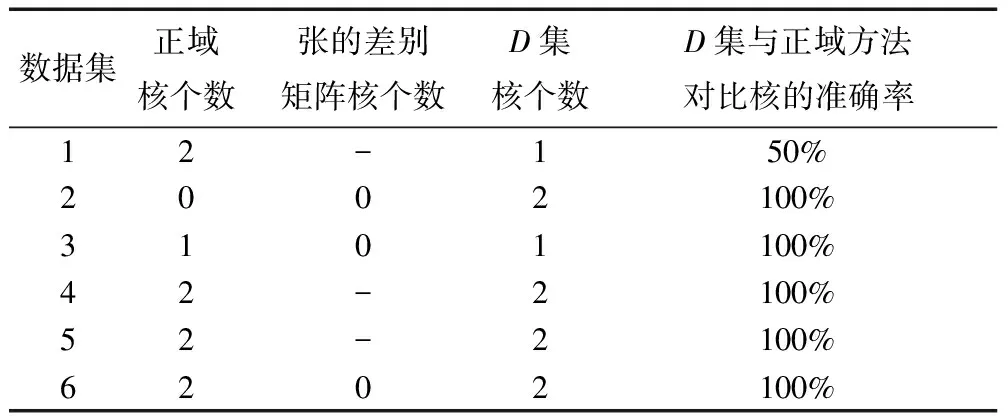
表6 求核属性结果

上述实验中，因为差别矩阵的方法适用于不完备的决策信息表，所以用“-”代表决策表是完备的。从实验结果可以看出，本文的算法和基于正域的求核属性算法得到的核几乎完全相同，只有部分数据由于去除了单个属性后，仍然得不到核约简，但是通过D集的运算，可以得到核集，说明了D集的可用性。数据集2中可以明显的看出，决策表是适用于差别矩阵方法的，但是得不到核，而正域的方法也同样得不到核，经过D集算法的运算，可以得到核，说明算法的有效性。同理可以得到，数据集3和6，不适用于差别矩阵的方法，D集方法和正域方法得到的核是一样的，再次说明了D集算法的有效性。

5 结束语

在完备决策表中，用基于正域方法相对来说是比较有效的，但是不免有得不到核属性的情况；在不完备决策表中，通常用差别矩阵求核属性的方法是比较好的，但是对有些数据集，此方法就显得不那么有效。本文从一致到不一致的角度，全面考虑决策表的特点，提出了一种基于D集的差别矩阵的求核方法，即在一致表时直接用D集和在不一致表时用差别矩阵、当差别矩阵得不到核属性时再用D集来求核的方法。实验结果表明，该算法能更有效的对决策系统进行约简，获得较好的核结果。

【参 考 文 献】

[1] 张国清，郑雪峰，张明德，等.粗糙集中不同核的比较研究[J]，小型微型计算机系统，2012，1(1)121-122.

[2] Deng D，Huang H，Li X.Comparision of various types of reductions in inconsistent systems[J].ACTA Electronica Sinica，2007，35(2)：252-255.

[3] Xu Z，Yang B，Song W，et al.Comparative research of different attribute reduction definitions[J].Journal of Chinese Computer System，2008，29(5)：848-853.

[4] Pawlak Z.Rough set[J].Communication of the ACM，1995，38(11)：89-95.

[5] 王国胤，于 洪，杨大春.基于条件信息熵的决策表[J].计算机学报，2002，75(7)：759-766.

[6] Hu X，Cercne N.Learning in relational databases：a rough set approach[J].International Journal of Computional Intelligence，1995，11(2)：323-338.

[7] Zhang W，Mi J，Wu W.Knowledge reductions in inconsistent information systems[J].Chinese Journal of Computer，2003，26(1)：12-18.

[8] 余承依，李进金.变精度粗糙集β下近似属性约简？[J]山东大学学报(理学版)2011.46(11)：17-21.

[9] 黄国顺，曾凡智.不一致决策表各种属性约简的不一致性分析与转化[J].小型微型计算机系统，2008，29(4)：703-708.

[10] 张迎春，王宇新，郭 禾.基于有序差别集和属性重要性的属性约简[J].计算机科学2011，38(10)：243-246.

[11] Pawlak Z.Rough set theory and its application to data analysis[J].Cybernetics and Systems，1998，29(7)：661-668.

[12] 王 珏.粗糙集理论及其应用研究[D]，西安：西安电子科技大学2005：1-5.

[13] 苗夺谦，李道国.粗糙集理论、算法与应用[M].清华大学出版社，2008.

[14] 王国胤.Rough理论与知识获取.西安交通大学出版社.2001.

[15] 张文修.粗糙集理论与方法.北京：科技出版社，2001.

[16] 叶东毅，陈昭炯.一个新的差别矩阵及其求核方法[J].电子学报，2002，30(7)：1086-1088.

[17] 杨 明，孙志挥.改进的差别矩阵及其求核方法[J].复旦学报(自然科学版)，2004，43(5)：865-869.

[18] 张振琳，黄 明.改进的差别矩阵及其求核方法[J].大连交通大学学报，2008，29(4)：79-82.