异方差对生物量模型构建的影响

杨嘉龙，肖生苓

(东北林业大学 工程技术学院，哈尔滨 150040)

自国际林联(IUFRO)1994年出版《国际森林监测指南》将生物量列为全球、区域和国家级森林资源监测的重要内容，越来越多的专家和学者提出了更新的生物量研究方法和理论，从变量选取到模型优化，生物量模型经历了从线性到非线性的结构转变。目前，应用最广泛也最被认可的是建立非线性的相容性生物量模型[1-5]。非线性模型对生物量的拟合效果比线性模型好，模型评价指标更高，更加符合林木的生长规律。相容性生物量模型通过以总量或树干生物量为基础的分级控制理论，能够很好的解决的总量和分量不相容的问题，而且模型检验指标满足建模要求。

非线性生物量模型的构建不同于线性生物量模型，其中最主要的原因就是非线性模型中变量的方差非齐性，线性生物量模型的构建就是基于方差齐性的假设前提，模型的误差项期望Eζ=0，得到线性模型的最优估计。而实际中，误差项的方差随自变量的变化而变化，如果忽略了模型中的异方差性，将会造成模型的参数估计值变化，不仅降低模型的估计精度，还会使估计值的检验和置信区间失效。为此，对模型的异方差检验和消除就显得尤为重要。

1 生物量模型中异方差的检验

由于调查数据往往存在测量误差，以及样本数据具有的个体差异性和建模模型的忽略因素，导致估计结果存在异方差性，在数据处理时，往往首先要检验误差项间是否有异方差存在，从而不影响模型的建立和参数的估计。可采用的检验方法有：图示检验法、帕克(Park)检验、巴特利特(Bartlett)检验、格莱泽(Glejser)检验、斯皮尔曼(Spearman)等级相关检验、戈德菲尔特-匡特(Goldfelt-Quandt)检验、布劳特-陪干-戈弗雷(Breusch-Pangan-Godfrey)检验、怀特(White)检验、ARCH(自回归条件异方差)检验、Wald检验、拉格朗日乘数检验和似然比检验[6]。其中，比较常用的是图示检验法、格莱泽(Glejser)检验、斯皮尔曼(Spearman)等级相关检验和怀特(White)检验。

1.1 图示检验法

图1 几种可能存在异方差的残差示意图

图示检验法虽然简单直观，但是只能够作为一种趋势的判定，不能通过图形看出引起异方差的变量，也得不到异方差的具体形式。

1.2 格莱泽(Glejser)检验

格莱泽(Glejser)检验是基于残差和解释变量间有显著成立的关系，如果方程存在异方差，那么异方差与解释变量的幂相关，假设异方差σi与第j个解释变量的关系如下：

(1)

由于异方差σi是经过检验后计算所得，格莱泽利用残差绝对值|ei|代替异方差σi，得到：

(2)

假如δ1=0，则可以认为异方差σ1与xi无关，即随即扰动项ui的方差与xj无关；δ1≠0，则随即扰动项ui的方差与xj的变化相关。异方差检验就转化为对δ1是否为0的检验，用T检验，如果参数δ1显著的不为0，则认为存在异方差。

此检验不仅能对异方差的存在作出判断，而且还能得到异方差随变量变化的具体形式，检验需要大量样本数据，而且误差项本身可能含有异方差。

1.3 斯皮尔曼(Spearman)等级相关检验

斯皮尔曼(Spearman)等级相关检验不用考虑模型参数，类似于格莱泽(Glejser)检验，通过检验残差和解释变量是否有显著关系，来判定异方差性。基于公式(1)将求得的随机变量的残差ei取绝对值，并与xi以升序或降序排列，按斯皮尔曼(Spearman)等级相关系数计算公式：

(3)

式中：Di=xi-ei，N为样本个数。

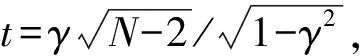
检验需要对残差和解释变量进行排序，样本容量过小会导致数据变异程度较大，降低检验可信度，而且此检验也无法给出异方差的具体形式[7]。

1.4 怀特(White)检验。

怀特检验能够将残差与不同形式的自变量结合起来，建立多元回归方程，其基本多元回归方程形式如下：

yi=δ0+δ1x1i+δ2x2i+δ3x3i+…+σnxni+ui。

(4)

再通过建立辅助回归模型的方式来判断回归方程的异方差性，假设自变量含3种形式，其辅助回归模型形式[8]为：

(5)

以上常用检验除格莱泽(Glejser)检验能得到异方差的具体形式，其余检验只能验证异方差性，图示检验可以依靠SPSS、SAS、MALTABLE等统计软件直接给出，应用最为普遍。

2 异方差的消除

通过上述检验，可以知道误差项是否具有异方差性，而且异方差的存在并不影响普通最小二乘法(Ordinary Least Squares，简称OLS)估计量的无偏性，但是会造成估计量的方差变大，导致通常假设的检验值失效。所以，对已经验证的异方差要采用办法去消除，以保证得到的模型具有最优的无偏估计。通常采用加权最小二乘法(The Weighted Least squares，简称WLS)、改变变量形式或重新设定模型这三种方法，这里只介绍最简单和最常用的方法——加权最小二乘法(WLS)。

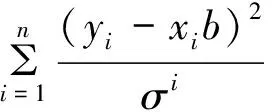
应用加权最小二乘法消除异方差已被得到广泛证实。采用加权最小二乘法最回归估计在消除异方差的同时，能够保证模型不含系统误差，其权函数形式可由变量本身构造，方便适用[10]。模型的拟合结果与普通最小二乘法相比，各项指标均有明显改善[11]。如果假定因变量yi的方差与自变量xi的某种形式成一定比例，权函数可以定义为wi=1/f(xi)消除异方差，但是要想得到准确具体的f(xi)形式就相对比较困难[12]。在实际应用WLS时，常以SPSS、Eviews等统计软件为工具，绘制残差图或对消除异方差的权函数进行探讨，理论上的最优权函数应该是与最大对数似然函数相应的取值[13]。

3 实例分析

以77株落叶松树干生物量建模数据为例，拟合的单木树干生物量优势方程形式为W树干=a(D2H)b，用此经验模型作为分析异方差的基础模型，通过SPSS软件绘制的残差图可以看出方程存在异方差性，如图2(a)所示。

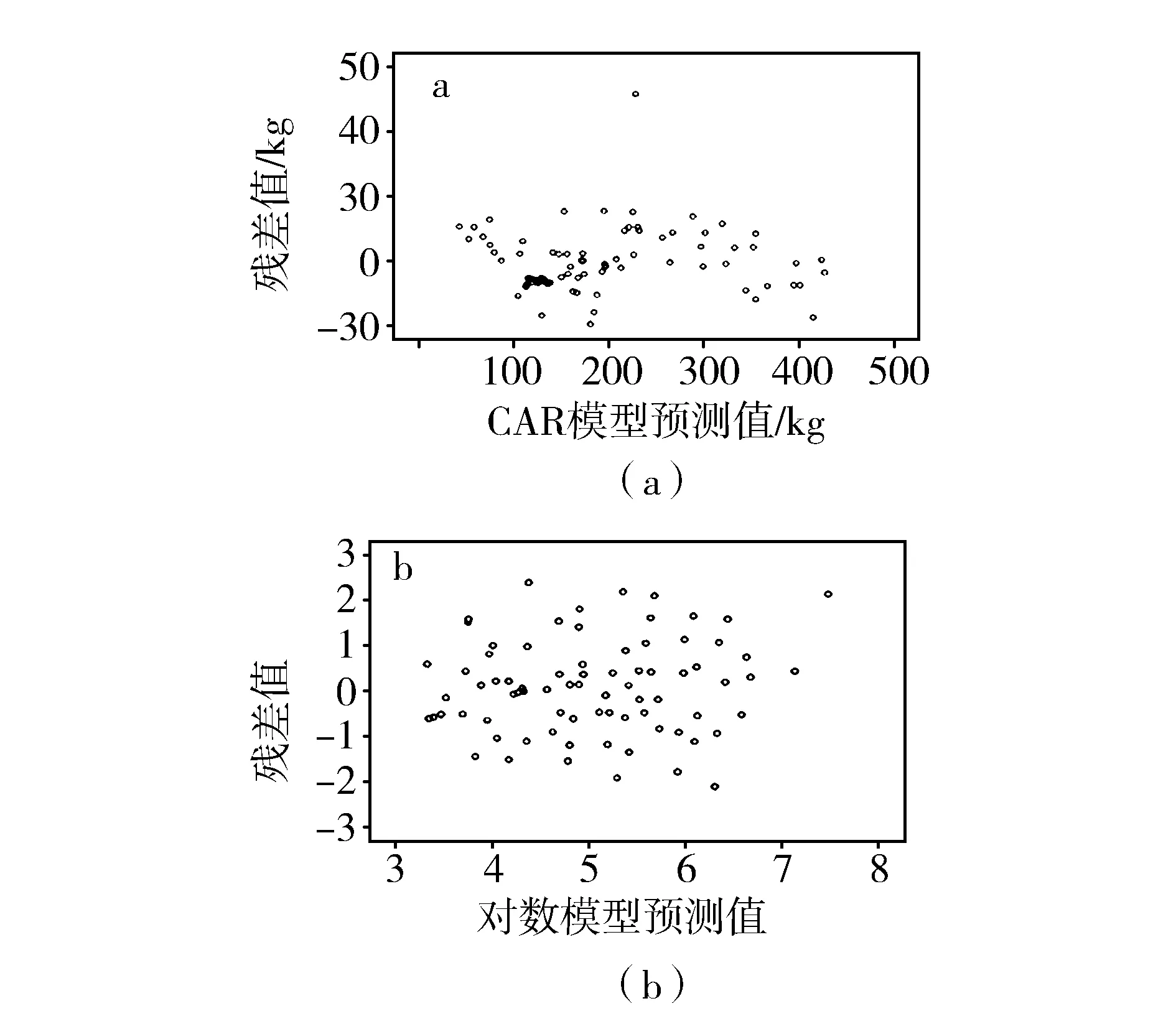
图2 存在和消除异方差的树干模型残差图

对模型异方差的消除分两个部分，首先是对经验模型进行对数转换，消除基于OLS下假设误差期望为0而造成的参数偏小和异方差性，如图2(b)所示。其次，建立树干相容性生物量模型，做到总量和各分量和相等，为了消除模型间的度量误差和异方差，要对干材和树皮生物量方程进行非线性联合估计，复杂生物量模型异方差的消除采取构造权函数的方法，鉴于一元回归方程与二元回归权函数方程对消除异方差的效果差别不大，这里采用由胸径D和树干生物量预估残差值方差1.06构造的一元回归方程作为权函数方程，即权函数为G=1/D1.06，模型通过决定系数(R2)、估计值的标准差(SEE)、平均估计误差(MPE)、平均相对偏差(ME)、平均相对偏差绝对值(MAE)以及预估精度(P)作为选择最优模型的检验指标。消除异方差的树干生物量模型拟合和检验结果，见表1。

通过表1可以看出，消除异方差后的对数模型和相容性生物量模型SEE值减小，说明采用模型转换和加权函数的方法是可行有效的，而且对模型的预估效果起到了很好的作用。

表1 消除异方差的树干生物量模型拟合结果和检验结果统计

4 结 论

生物量建模过程中，往往存在着异方差性，会导致采用普通最小二乘法进行回归所得估计值有偏，参数值和有效区间失真。这就需要对误差项可能存在的方差性进行检验，并采取有效的消除方法，文章通过实例证明检验和消除异方差的方法是行之有效的，而且能够保证系统模型的建模要求。

【参 考 文 献】

[1] 唐守正，张会儒，胥 辉.相容性生物量模型的建立及其估计方法研究[J].林业科学，2000，36(1)：20-27.

[2] 胥 辉，刘伟平.相容性生物量模型研究[J].福建林学院学报，2001，21(1)：18-23.

[3] 罗云建.森林生物量的估算方法及其研究进展[J].林业科学，2009，45(8)：129-134.

[4] 翟 畅，胡润田，范文义.森林水源县生态效益的估算与评价研究[J].森林工程，2012，28(4)：69-72.

[5] 曾伟生，唐守正.利用度量误差模型方法建立相容性立木生物量方程系统[J].林业科学研究，2010，23(6)：797-802.

[6] 白雪梅.异方差性的检验方法及评述[J].东北财经大学学报，2002(6)：26-29.

[7] 徐唐先.关于等级相关中斯皮尔曼公式[J].统计与决策，1995，22-23.

[8] 申屠惠良.使用怀特检验判断生物量模型的异方差性[J].浙江林业科技，2012，32(3)：43-45.

[9] 龚秀芳.回归模型中异方差数据的处理[D].上海：华东师范大学，2002.

[10] 唐守正，胥 辉.关于生物量模型中的异方差问题[J].林业资源管理，1999(1)：46-49.

[11] 郑春茂.加权回归及权函数的变换在生物量建模中的应用[J].华东森林经理，2012，26(2)：77-79.

[12]胥 辉.生物量模型方差非齐性研究[J].西南林学院学报，1999，19(2)：73-77.

[13]宋廷山，李 杰.回归模型的异方差性消除方法探讨[J].统计教育，2007(4)：6-7.