三阶非线性三点边值问题的正解

徐鑫，李德虎

(安徽大学 数学科学学院，安徽 合肥 230601)

0 引言

文献[1]考虑了下列三阶边值问题正解的存在性:

(1)

文献[2]考虑了下列三阶边值问题正解的存在性:

(2)

受到上面两篇文章的启发,本文考虑了不同边值问题(1)式正解的存在性问题,即

(3)

基本假设如下:

(H1)a∈C([0,1]→[0,+∞)),且存在t0∈[0,1],使得a(t0)≠0；

(H2)a∈C([0,1]→[0,+∞)),且存在t0∈[0,1],使得a(t0)≠0；

主要证明基于下面的不动点定理:

考虑E=C[0,1]，在E中构造如下锥P：

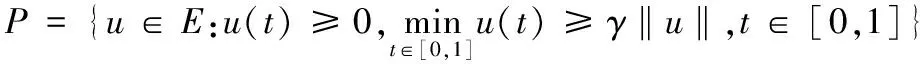
(4)

定义算子A：P→E

(5)

1 引理证明

边值问题(1.1)有解的充要条件是算子方程u=Au有不动点.

引理1.1 令y(t)∈C[0,1]，则边值问题

(6)

(7)

(8)

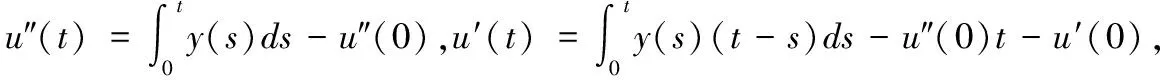
由边值问题可求得：

(9)

(10)

故A(P)⊂P

引理1.3 设条件(H1)(H2)成立，则A是P→P的全连续算子.

证明：由条件(H1)(H2)知：a(t),f(u)为连续函数，利用Arzela-Asxoli定理易验证A是P→P的全连续算子.其不动点即为(1.1)的解.

2 结论

定理2.1 假设条件(H1)(H2)成立，且f0=0,f∞=∞，则边值问题(1.1)至少存在一个正解.

(11)

令Ω1={u∈E:‖u‖≤h1}，故‖Au‖≤‖u‖，∀u∈P∩∂Ω1.

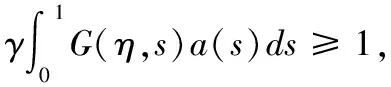
从而有

(12)

即有：‖Au‖≥‖u‖,∀u∈P∩∂Ω2

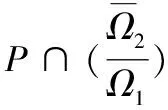
定理2.2 假设条件(H1)(H2)成立，且f0=∞,f∞=0，则边值问题(1.1)至少存在一个正解.

证明：定理的证明过程类似与定理(3.1)证明.

[1]Yongping Sun.Positive solutions for third-order three-point nonhomogeneous bound-ary value problems[J]. Applied Mathematics Letters, 2009,22(1):45-51.

[2]LiJun Guo , JianPing Sun, Ya-Hong Zhao, Existence of positive solutions for nonlinear third-order three-point boundary value problems[J].Nonlinear Analysis, 2008，68(2):3151-3158.