不等式的加强及应用

山东省高青一中 (邮编：256300)

山东省高青县教研室 董 林 (邮编：256300)

本文约定：△ABC的三边长为a、b、c，三个内角为A、B、C，外接圆半径为R，内切圆半径为r，半周长为s，面积为△，∑表示循环和，∏表示循环积.

①

本文将不等式①加强为：

②

利用Gerresten不等式[1]：

16Rr-5r2≤s2≤4R2+4Rr+3r2.

立得不等式②成立，证毕.

由著名的Euler不等式R≥2r，可知不等式②强于不等式①.

推论1在△ABC中，有

③

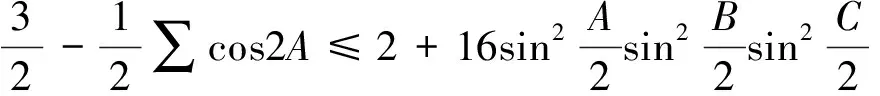
推论2在△ABC中，有

∑a2≤8R2+4r2

④

证明在不等式②的右边利用正弦定理就可得到不等式④.

推论3在△ABC中，有

⑤

证明由Colombier-Doucet不等式[3]

由不等式②利用正弦定理得：

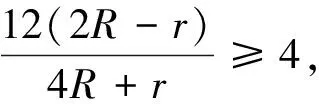
⑥

推论5在△ABC中，有

∏(b2+c2-a2)≤∏(b+c-a)2⑦

1 O.Bottema等著，单墫译.几何不等式[M].北京：北京大学出版社,1991

2 S.Nakajimc,Tohoku Math.J.25(1925)

3 G.Colombier-T.Doucet.Problem 1051.Nouv Ann.31(1872)，467