向心球轴承的负荷分布研究

沙 钊马 青

（1.上海飞机设计研究院，中国 上海 201210；2.华东师范大学，中国 上海 200062）

滚动轴承是采用滚动摩擦原理工作的支承件，具有摩擦力小、易于启动、升速迅速、结构紧凑，适应现代各种机械要求的工作性能和使用寿命以及维护保养简便等特点，在国民经济发展和国防建设中正起着越来越突出的作用，可以毫不夸张地说：轴承技术代表着世界整个工业的发展水平[1]。

滚动轴承的承载能力影响着生产效益、产品质量和操作者的安全。目前，机械设计中采用的滚动轴承，往往是根据经验的、保守的方法来选择。这样做虽然安全，但造成材料浪费，成本增加，设备笨重。因此，合理地分析计算滚动轴承的承载能力，并据此选用轴承，在工业生产中具有重要的意义。

1 数学模型建立

向心球轴承负荷分布如图1所示：

图1 向心球轴承负荷分布图[2]

图中Fr为向心球轴承所承受径向负载，ψ为该滚动体与最大负荷滚动体之间的夹角。

轴承上各滚动体所承受的最大载荷为Qmax，如式（1）所示。

z为轴承上滚动体数量，Jr为椭圆积分，如下式所示：

其中φ为负荷分布区夹角的一半，当轴承径向游隙ur=0时，φ=为轴承负荷分布系数：

上式中δmax为轴承滚动体最大变形量：

式中 v1，v2，E1，E2根据材料的不同而变化，为主曲率和，由下面两式：

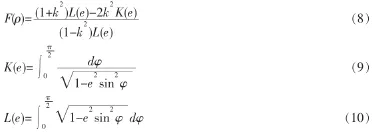
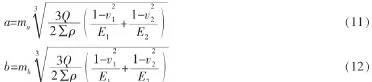
可以解出ma、mb，进而解出Kp，逐步求出向心球轴承所承受的罪的负荷Qmax。

由上述数学模型我们可以看出，如何通过主曲率函数F(ρ)求出偏心率 e，以及如何求出椭圆积分 K(e)、L(e)、Jr(ε)是上述数学模型得以解出的关键之处，也是该数学模型的难点。

2 计算准备

按通过牛顿迭代法[3]，可以得到主曲率函数F(ρ)与偏心率e之间的关系曲线如图2所示。

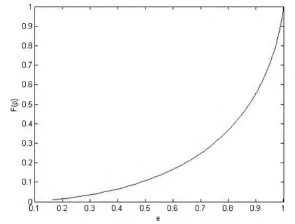
图2 主曲率函数F(ρ)与偏心率e的关系曲线

在已知偏心率e的情况下，可以得出K(e)、L(e)和与偏心率e的关系曲线如图3所示，其中虚线表示的是K(e)曲线，点线表示的是L(e)曲线。

在已知载荷分布系数ε的情况下，我们可以得出Jr(ε)曲线如图4所示。

图4 向心球轴承的Jr与ε的关系曲线

3 影响分析

针对轴承代号为6008的深沟球轴承，采用上述数学模型对其负荷分布进行计算，主要分析轴承径向游隙[5]、滚动体直径以及滚动体数量对滚动体上最大负荷的影响。待计算轴承的基本参数有：轴承外径D=68mm，轴承内径d=40mm，轴承宽度B=15mm，轴承所承受外加径向力大小Fr=15kN。

3.1 径向游隙对轴承负荷分布的影响

轴承其余参数：滚动体直径取Db=8mm，滚动体数量z=12。

图5为径向游隙变化时，滚动体所受最大负荷的变化情况。

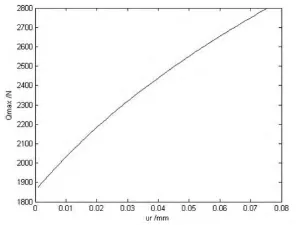
图5 向心球轴承的Q max与ur关系曲线

3.2 滚动体直径对轴承负荷分布的影响

轴承其余参数：径向游隙取ur=14μm，滚动体数量z=12。

图6为滚动体直径变化时，滚动体所受最大负荷的变化情况。

图6 向心球轴承的Q max与Db关系曲线

3.3 滚动体数量对轴承负荷分布的影响

轴承其余参数：径向游隙取ur=14μm，滚动体直径取Db=8mm。

图7为滚动体数量变化时，滚动体所受最大负荷的变化情况。

图7 向心球轴承的Q max与滚动体数目z关系曲线

4 结论

利由上述计算分析结果我们容易发现向心球轴承上的负荷分布与径向游隙、滚动体直径以及滚动体数目有着密切的关系，一般来说，径向游隙越小，滚动体直径越小，滚动体数目越多，则滚动体上所受的最大接触应力就越小。同时，径向游隙还影响着轴承的负荷分布范围，径向游隙越小，轴承的负荷分布范围就越大。

［1］毛尚涛.滚动轴承的发展状况与应用[J].济南纺织化纤科技,2005(1)：39-41.

［2］万长森.滚动轴承的分析方法[M].北京：机械工业出版社,1987.

［3］冈本纯三.球轴承的设计计算[M].黄志强,译.北京：机械工业出版社,2003.

［4］罗祝三,吴林丰.径向游隙对向心轴承性能的影响[J].机械设计,1993,10(4)：17-20.