艾尔布朗语义下的真谓词

熊 明

（华南师范大学政治与行政学院，广东广州510631）

塔斯基［Tarski 1936］提出了一阶语言的一种解释，这种解释允许使用任何个体对象作为变元的取值，不同的变元或常元可能以相同的对象作为它们的解释。这种解释现在已成为一阶语言的标准解释，被称为塔斯基语义。在塔斯基提出这种语义之前，法国逻辑学家艾尔布朗在对其“基本定理”（现称为艾尔布朗定理）的证明中，事实上也对一阶语言提出了一种解释。①塔斯基的论文发表于1935年，而艾尔布朗定理出现在艾尔布朗的博士论文[Herbrand 1930]（1929年4月完成，但因服兵役答辩直到1930年6月才完成），这篇论文甚至稍早于哥德尔关于完全性定理证明的那篇论文［1930年2月完成答辩］。参见［van Heijenoort 1967］，第 525、582页。在这种解释中，变元的取值只能是一阶语言中的项，各个项的解释就是项本身（因而，不同的项——特别地，不同的变元或常元——必定被解释为不同的对象）。这种解释现在称为一阶语言的艾尔布朗语义。

从表面看来，艾尔布朗语义仅仅是塔斯基语义的一种特殊情形。因此，虽然艾尔布朗定理是一阶逻辑中最基本的结果之一，但是艾尔布朗语义本身似乎并没有引起逻辑学家足够的重视。美国斯坦福大学的T．Hinrichs和M．Genesereth教授在文［Hinrichs&Genesereth 2006］中的研究表明，艾尔布朗语义与塔斯基语义在可判定性、逻辑后承关系等方面是不同的。

上述种种差异自然是由不同语义解释造成的。一阶语言中任何概念只要依赖于语义都可能会在塔斯基语义和艾尔布朗语义下有所不同。而真谓词作为语义中最基本的概念之一自然会被纳入到上述两种语义的框架之内。真谓词在艾尔布朗语义下是否具有不同于塔斯基语义中的表现呢？这个问题似乎在文献中还没有得到深入的研究，本文就是要想对这一问题进行初步的探索，指出艾尔布朗语义下的真谓词概念确实是值得注意的。

一、艾尔布朗语义

一阶语言中的初始符号、项、公式等句法对象一如往常规定。需要补充的是，为了使艾尔布朗语义不至于过于平庸，这里约定一阶语言中个体常元不空。注意，一阶语言中的语句指的是闭公式，即不含自由变元的公式。

我们知道，在塔斯基语义中，为了能对语句进行赋值，必须给出一定的模型对语句中的非逻辑符号做出解释，同时还必须通过指派对变元指定对象。这里主要的麻烦在于，虽然语句的赋值独立于指派，但是一般情况下，必须在模型和指派下对所有的公式进行赋值，然后才能在模型下对语句进行赋值。艾尔布朗语义就不存在这样的问题，我们可以直接对语句进行赋值。

我们规定，对于一个一阶语言L，只要确定L中原子语句的一个集合，就给出了L的一个艾尔布朗模型。在某个艾尔布朗模型M下，按如下方式规定原子语句的可满足性：形如s=t的原子语句在M下可满足，当且仅当项s和t作为符号串完全相同；形如Pt1…tn的原子语句在M下可满足，当且仅当项s和t作为符号串完全相同。由联接词联接得到的复合语句的可满足性如常规定，略去。量词语句的可满足性规定如下：形如∀xA的语句在M下可满足，当且仅当对L中每个闭项t，A（t）都在M下可满足；形如∃xA的语句在M下可满足，当且仅当L中存在某个闭项t，使得A（t）在M下可满足。

相应于上述可满足概念，可规定逻辑后承。如果任何满足语句集∑的艾尔布朗模型也一定满足语句A，那么就称A是∑的一个逻辑后承，又可称∑衍推出A。为明确起见，艾尔布朗模型下的可满足及逻辑后承概念加前缀“H-”，而塔斯基语义下的可满足及逻辑后承概念加前缀“T-”。

如［Hinrichs&Genesereth 2006］文所指出，在塔斯基语义下，一阶公式的可满足性是半可判定的，但在艾尔布朗语义下，一阶公式的可满足性不是半可判定的；在塔斯基语义下，逻辑后承关系具有紧致性，但在艾尔布朗语义下，逻辑后承关系不具备紧致性；在塔斯基语义下，自然数结构中的真语句是不能有穷可公理化的，但在艾尔布朗语义下，自然数结构中的真语句是有穷可公理化的。

作为例子，考虑这样一个一阶语言，其中非逻辑符号只有一元谓词P和个体常元a。众所周知，Pa不是∃xPx的T-逻辑后承。然而，Pa却是∃xPx的H-逻辑后承，理由是满足∃xPx的艾尔布朗模型只有{Pa}一个。再考虑一阶语言，其中除含上述P和a外，还含一个一元函数符f。因为这个语言中的闭项是a、fa、ffa如此等等，所以，∀xPx是集合{Pa，Pfa，Pffa，…}的一个 H-逻辑后承。然而，很明显，{Pa，Pfa，Pffa，…}的任何有穷子集都不会H-衍推出∀xPx。由此可见，与T-逻辑后承不同，H-逻辑后承不满足紧致性。

二、塔斯基T-模式

下面转入本文的主题：艾尔布朗语义下的真谓词。为此，先规定皮亚诺算术的一个形式语言LN，其中除等词=外，还含有二元谓词Less、三元谓词Add、Mult、一元函数符S以及个体常元0。注意，在艾尔布朗语义下，因为只有那些完全相同的项才是相等的，所以不能使用函数符来表示加法和乘法运算（不然的话，甚至如0+0=0这样的语句在艾尔布朗语义都是不可满足的）。在LN中添加一元谓词T得到的语言记为。这个语言就是我们考虑真谓词的一阶语言。除非特别声明，以下所说项、公式等皆指中的项、公式。用记号‘A’表示公式A的哥德尔数。

这里，T不是一个普通的谓词符，而是用来表示真谓词的符号。那么，什么时候T才能被视作是真谓词呢？按照塔斯基的思想，唯有下一模式对某个语言中的每个语句A都成立，才能认为T是该语言的真谓词：T‘A’当且仅当A（［Tarski 1936］，155-156）。此模式就是著名的塔斯基T-模式。此模式在塔斯基语义下的表现形式如下：

X作为T的解释，很自然应当包含且只包含中所有在N与X构成的解释中为真的语句。换句话说，式子（1）应对中每个语句A成立，只有这样，T的解释X才被认为是的真谓词。然而，塔斯基证明，这是不可能做到的，因为若不然，则在中，可以构造这样的语句λ，满足：

这样，把λ代入到式子（1）中会导致矛盾。这个结论常被称为“塔斯基定理”，而证明中所用语句λ因它断定它自己不真，故相当于说谎者语句。

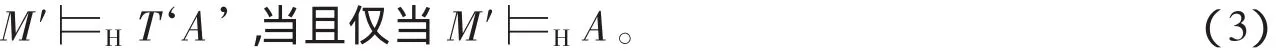
在此情况下，使用先前提到的语句λ，同样可以导出矛盾。因此，在的艾尔布朗语义下，塔斯基定理同样成立：不可能包含它自身的真谓词。

这里顺便指出，艾尔布朗语义下的塔斯基T-模式与塔斯基语义下的T-模式似乎并无太大的区别，但是对于［Hsiung 2009］所提出的T-模式的一个推广，情况似乎并不明了，究竟如何在艾尔布朗语义下表达T-模式的这个推广似乎是值得深入研究的问题。

三、亚布鲁悖论

美国逻辑学家亚布鲁（S．Yablo）在文［Yablo 1993］中提出了以他名字命名的悖论。这个悖论含有可数无穷多个语句：Y（0），Y（1），……，每个语句都断定它后面的每个语句都不真。这些语句蕴涵矛盾，这是因为假设Y（0）为真，根据Y（0）所说，对于k＞0，Y（k）为假。因而，一方面，Y（1）为假，另一方面，对于所有k＞1，Y（k）为假。这样，Y（1）为真，与Y（1）为假矛盾。于是，Y（0）必为假。同理，这个语句的其他每个语句都为假，因而，Y（0）又必为真，矛盾。

首先注意，语句集Υ是PA一致的。这是因为在PA中，从集合Υ的任何有穷子集都不会推出矛盾，然而PA的推演满足紧致性定理，因此，整个Υ就是PA一致的。然而，集合Υ是PAω不一致的（见［Ketland 2005］，299）。这一点可以从上一节的标准塔斯基解释不满足Υ可以看出。因而，在塔斯基语义下，只有PA的非标准模型能满足Υ。换言之，T的解释只有包含某个非标准数才能使Υ中语句（在非标准的塔斯基语义下）都为真。

四、语言层次

众所周知，为了突破塔斯基定理的限制，塔斯基本人采用了语言分层的方式来规定真谓词。事实上，仅需把T解释为LN中所有在N中为真的语句的哥德尔数构成的集合X，则式子（1）一定对中任意语句A都成立。在这个意义上虽然不能含有它自身的真谓词，但是它包含LN的真谓词因而被称为的元语言。

分层的想法同样适用于艾尔布朗语义。回到先前提出的艾尔布朗语义中的底模型M。注意，M中不含任何带真谓词符的语句，因此T在M中实际被解释为空谓词。但是，若规定M1是M与所有使得M⊨HA成立的语句T‘A’的并集，则对的任意语句A，都有，当且仅当M⊨A。特别地，对LN的语句，有，当且仅当M1⊨A。因此同样包含了这样的T，它被解释为LN的真谓词。

对语言进行分层规定真谓词的做法历来为学者所诟病，其中毛病之一如克里普克指出，这种做法无法对超穷的层次进行规定（见［Kripke 1975］，59～61）。克里普克批评的要点在于超穷层次要求对之前层次的真谓词外延进行累积，但真谓词的外延累积会导致矛盾。这一点是熟知的事实。此处，我们说明类似的累积在艾尔布朗语义也同样导致矛盾，甚至无需等到超穷层次，这种矛盾在第二层次就会产生。

为此，我们规定M2是M1与所有使得M1⊨HA成立的语句T‘A’的并集。考虑说谎者语句λ，因为T‘λ’不在M中，所以，M⊨Hλ。由此，T‘λ’在M1中，所以，M1⊨Hλ不成立。根据M2的规定，T‘λ’不在M2中。但由此由M1累积出来的，T‘λ’必在M1中，这就出现矛盾了。由此可见，在的艾尔布朗语义中，模型如果按累积规定下去至多到第一个层次就必须终止。

能使层次一直进行下去的办法主要有两种，一种是按克里普克的归纳构造方法，修改模型上的赋值引入真值空缺（见［Kripke 1975］）；另一种就是按古普塔和赫兹伯格的修正理论，在构造模型的时候不进行累积只进行修正（见［Gupta 1982］和［Herzberger 1982］）。本文限于经典逻辑，所以只考虑第二种办法。

在艾尔布朗语义中，可这样来规定不具累积效应的模型：以M作为起点，设之为；然后，对任意序数α，规定就是所有使得成立的语句T‘A’的并集；最后，对极限序数α，规定就是前面所有阶段的下极限，也就是说包含语句A，当且仅当存在一个小于α的序数γ，使得对任意大于γ但小于α的都包含A。通过这样的规定，我们就不难在艾尔布朗语义中展开修正理论了。

五、结论

前面的分析总结起来，有以下几点：塔斯基T-模式在艾尔布朗语义中的表达类似于塔斯基语义中的表达，而且使用说谎者悖论同样能够在艾尔布朗语义中得到塔斯基定理；亚布鲁悖论在塔斯基非标准模型中可以得到满足，但是在艾尔布朗语义中却是不可满足的；语言分层的思想在（经典）塔斯基语义中到第ω阶段一般情况下不能继续，但在艾尔布朗语义中甚至到第二阶段就不得不终止。

可以看到，艾尔布朗语义下的真理论与塔斯基语义下的真理论既有共通之处，又有某些让人感兴趣的差异。当然，这个对照分析还比较初步，我们主要的目的是抛砖引玉，希望引起读者注意，艾尔布朗语义下的真理论本身还是有许多问题值得考虑的。

[1]Gupta，A．Truth and paradox[J]．Journal of Philosophical Logic，1982，11（1）．

[2]Herbrand，J．Investigations in proof theory：The properties of true propositions[M]//van Heijenoort，J．（ed．）From Frege to Gödel：A Source Book in Mathematical Logic，1879-1931（Source Books in the History of the Sciences）．Cambridge：Harvard University Press，1967，525～581．

[3]Herzberger，H．G．Notes on naive semantics[J]．Journal of Philosophical Logic，1982，11（1）．

[4]Hinrichs，T．，Genesereth，M．Herbrand Logic[OL]．http://www．cs．uic．edu/～hinrichs/papers/hinrichs2006herbrand．pdf，2006-02．

[5]Hsiung，M．Jump Liars and Jourdain’s Card via the relativized T-scheme[J]．Studia Logica，2009，91（2）．

[6]Ketland，J．Yablo’s paradox and ω-inconsistency[J]．Synthese，2005，145（3）．

[7]Kripke，S．A．Outline of a theory of truth[M]//Martin，R．L．Recent Essays on Truth and the Liar Paradox．Oxford：Oxford University Press，1984，53～82．

[8]Tarski，A．The concept of truth in formalized languages[M]//Woodger，J．H．（tr．）Logic，Semantics，Metamathematics：Papers from 1923 to 1938．Oxford：Clarendon Press，1956，152～278．

[9]Yablo，S．Paradox without self-reference[J]．Analysis，1993，53（4）．