一类解析函数类的凸性
李小飞,熊良鹏
(1.长江大学工程技术学院,湖北 荆州434020;2.成都理工大学工程技术学院,四川 乐山614000)
0 引言
本文中用U表示复平面内的单位圆盘U={z:|z|<1,z∈C},并用H(U)表示U内的解析函数族,S表示U内的单叶函数族.记
并记A(1,1)=A.定义

为p叶α阶星象函数类[1-2],并记S*1(1,α)=S*(α)表示传统意义下的α阶星象函数类,S*1(1,0)=S*表示传统意义下的星象函数类.定义
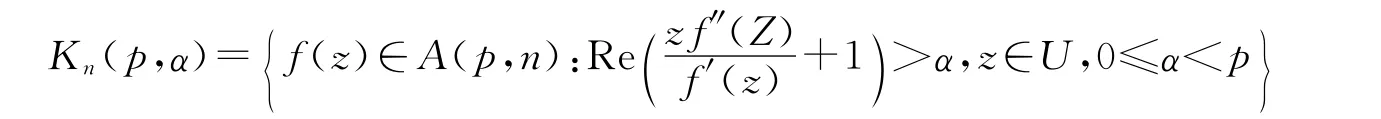
为p叶α阶凸函数类[3-4],并记K1(1,α)=K(α)表示传统意义下的α阶凸函数类,K1(1,0)=K表示传统意义下的凸函数类.由定义容易知道,Kn(p,α)⊂S*n(p,α)⊂S.
Frasin[5]定义了A中的函数类B(μ,α):


Macarie V M等[6]定义了积分算子函数:
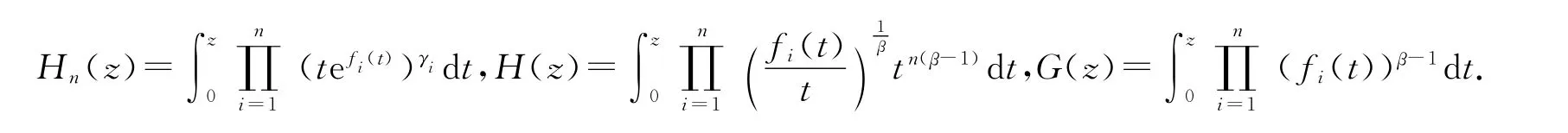
本文中新定义一类函数类BS(n,p,μ,α):

当μ=1时,BS(n,p,1,α)当p=n=1时,BS(1,1,μ,α)=B(μ,α);当p=n=1,μ=0时,BS(1,1,0,α)⊂R(α),许多作者[7-11]研究过这些函数类的性质.本文中利用解析函数理论,研究得到函数类BS(n,p,μ,α)中积分算子函数Hn(z),H(z),G(z)的凸性和α阶凸性.
1 主要结果
引理1.1[12]设函数f(z)是圆盘UR={z∈C,|z|<R}内的解析函数且|f(z)|≤M,M是回定的非负实数.若f(z)在z=0处有大于或等于m阶的零点,则等号(不等式中z≠0)成立当且仅当这里θ为常数.
定理1.2 设fi(z)∈BS(n,p,μi,αi),μi≥0,0≤αi<p,i=1,2,…,n,若|fi(z)|≤Mi,Mi≥1为常数,则Hn(z)∈Kn(p,δ),这里
定理1.2的证明 假设fi(z)∈BS(n,p,μi,αi),i=1,2,…,n,则
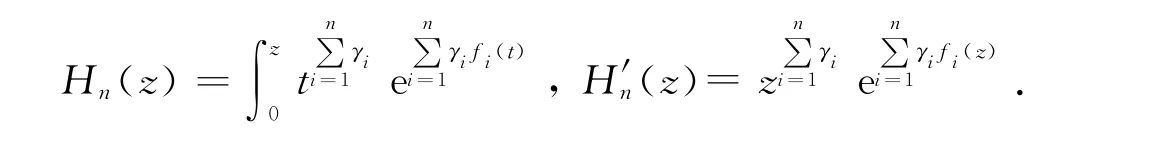
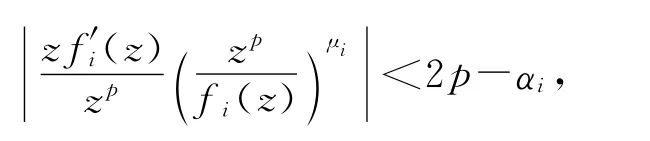

令
因此,Hn(z)∈Kn(p,δ).
推论1.3 设fi(z)∈BS(n,p,μi,αi),μi≥0,0≤αi>p,i=1,2,…,n,若|fi(z)|≤M,M≥1为常数,则Hn(z)∈Kn(p,δ),这里则即因此

推论1.3的证明 在定理1.2中令Mi=M即可.
推论1.4 设fi(z)∈B(μi,αi),μi≥0,0≤αi<1,i=1,2,…,n,若|fi(z)|≤Mi,Mi≥1为常数,则Hn(z)∈这里
推论1.4的证明 在定理1.2中令n=p=1即可.
推论1.5 设fi(z)∈R(αi),0≤αi>1,i=1,2,…,n,则Hn(z)∈K(δ),这里
推论1.5的证明 在定理1.2中令n=p=1,μi=0,i=1,2,…,n即可.
推论1.6 设fi(z)∈S*n(p,αi),0≤αi<p,i=1,2,…,n,若|fi(z)|≤Mi,Mi≥1为常数,则Hn(z)∈Kn(p,δ),这里
推论1.6的证明 在定理1.2中令μi=1,i=1,2,…,n即可.
定理1.7 设fi(z)∈BS(n,p,μi,αi),μi≥0,0≤αi<p,i=1,2,…,n,若|fi(z)|≤Mi,Mi≥1为常数,则H(z)∈Kn(p,δ),这里1]+n|β-1|≤1,β∈C/{0}.
定理1.7的证明 假设fi(z)∈BS(n,p,μi,αi),i=1,2,…,n,则
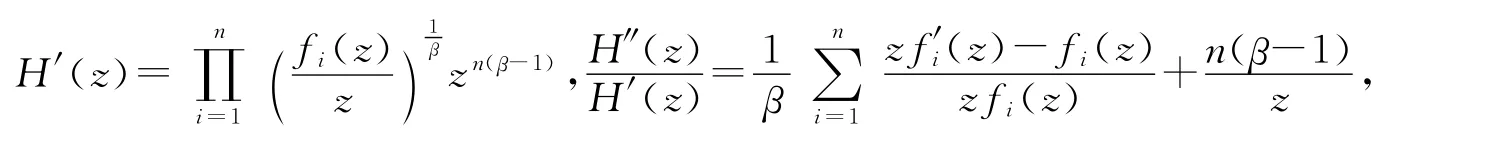
且
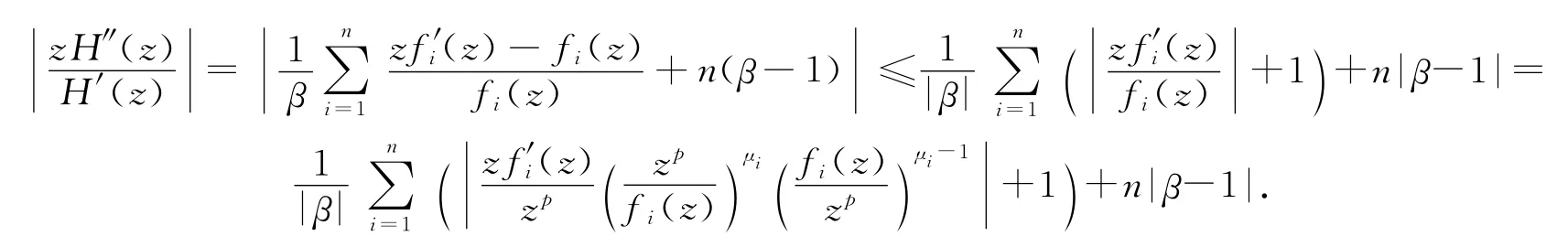
由引理1.1可知,对i=1,2,…,n,有且|z|p<1.又fi(z)∈BS(n,p,μi,αi)知,所以,
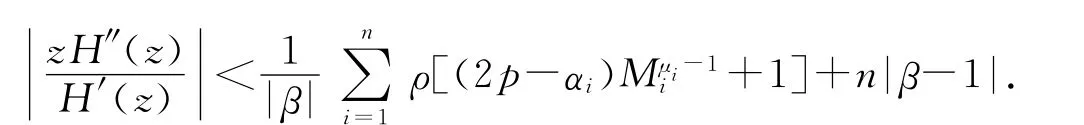
因此,H(z)∈Kn(p,δ).
推论1.8 设fi(z)∈BS(n,p,μi,αi),μi≥0,0≤αi<p,i=1,2,…,n,若|fi(z)|≤M,M≥1为常数,则H(z)∈Kn(p,δ),这里1]+n|β-1|≤1,β∈C/{0}.
推论1.8的证明 在定理1.7中令Mi=M,i=1,2,…,n即可.
推论1.9 设fi(z)∈B(μi,αi),μi≥0,0≤αi<1,i=1,2,…,n,若|fi(z)|≤Mi,Mi≥1为常数,则H(z)∈K(δ),这里1,β∈C/{0}.
推论1.9的证明 在定理1.7中令n=p=1即可.
推论1.10 设fi(z)∈S*n(p,αi),0≤αi<p,i=1,2,…,n,若|fi(z)|≤Mi,Mi≥1为常数,则H(z)∈β∈C/{0}.
推论1.10的证明 在定理1.7中令μi=1,i=1,2,…,n即可.
定理1.11 设fi(z)∈BS(n,p,μi,αi),μi≥0,0≤αi<p,i=1,2,…,n,若|fi(z)|≤Mi,Mi≥1为常数,
则G(z)∈Kn(p,δ),这里Kn(p,δ),这里
定理1.11的证明 假设fi(z)∈BS(n,p,μi,αi),μi≥0,0≤αi<p,由G(z)的定义,知由引理1.1和fi(z)的定义可得,
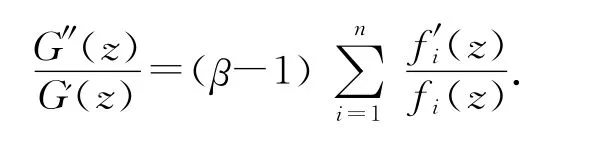
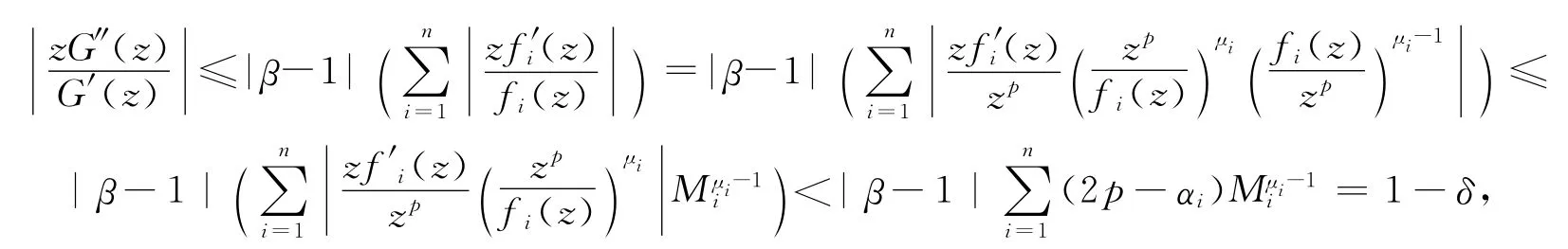
推论1.12 设fi(z)∈BS(n,p,μi,αi),μi≥0,0≤αi<p,i=1,2,…,n,若|fi(z)≤M,M≥1为常数,则G(z)∈Kn(p,δ),这里
推论1.12的证明 在定理1.11中令Mi=M,i=1,2,…,n即可.
推论1.13 设fi(z)∈B(μi,αi),μi≥0,0≤αi<1,i=1,2,…,n,若|fi(z)|≤Mi,Mi≥1为常数,则G(z)∈K(δ),这里
推论1.13的证明 在定理1.11中令n=p=1即可.
推论1.14 设fi(z)∈S*n(p,αi),0≤αi<p,i=1,2,…,n,若|fi(z)|≤Mi,Mi≥1为常数,则G(z)∈Kn(p,δ),这里
推论1.14的证明 在定理1.11中令μi=1,i=1,2,…,n即可.
[1]扬定恭.关于具有负系数的p叶星象函数的注记[J].纯粹数学与应用数学,1993,9(1):119-122.
[2]刘金林.关于p叶星象函数和Bazilevi函数的若干注记[J].扬州师范学院学报:自然科学版,1996,16(2):12-15.
[3]刘金林.关于p叶解析函数的若干结果[J].工科数学,1992,57(2):165-175.
[4]扬定恭.亚纯p叶凸象函数的子类[J].数学研究与评论,2000,20(2):215-219.
[5]Frasin B A,Jahangiri J.A new and comprehensive class of analytic functions[J].Anal Univ Oradea Fasc Math,2008(15):59-62.
[6]Macarie V M,Breaz D.On the convexity of certain integral operator[J].Ann Funct Anal,2012,3(2):183-190.
[7]韦叶,隐建兰,刘金林.由线性算子定义的一类p叶解析函数[J].扬州大学学报:自然科学版,2006,9(1):5-8.
[8]武怀勤.由算子定义的p叶函数的子类[J].五邑大学学报,2001(3):1-4.
[9]仓交玲.由算子定义的一类p叶解析函数性质[J].大学数学,2011,27(2):57-61.
[10]Frasin B A,Darus M.On certain analytic univalent functions[J].Int J Math Csi,2001,25(5):305-310.
[11]Frasin B A,Jahangiri J M.A ner and comprehensive class og analytic functions[J].Analele Universitatii din Oradea,Tom XV,2008:61-64.
[12]Mayer O.Function theory of one complex variable[M].Bucuresti:Academy Press,1981.

