AuCrS2材料的第一性原理研究

杨辉，黄忠兵，2

（1.湖北大学物理学与电子技术学院，湖北 武汉430062；2.北京计算科学研究中心，北京100084）

0 引言

瑞士学者Schmid［1］在1994年明确提出了多铁材料的概念，即具有两种或两种以上初级铁性体特征的化合物称为多铁性材料.由于其性质的特殊性，不仅可以单独作为铁磁材料、铁电材料或铁弹材料使用，而且由于电极化、磁极化及铁弹性形变间的相互耦合作用使这类材料在存储器，传感器和声波转换器等领域有着巨大的应用前景.在多铁材料中，自发磁矩可以随外加磁场变化而翻转，从而实现信息存储.铁电性具有自发电极化，自发电极化可随外加电场变化而翻转.与目前广泛应用的磁性存储器相比，基于铁电材料的铁电随机读取存储器具有非挥发性和读取速度快等优点［2-3］.很多铁电体同时也是铁弹体，其电极化的改变通常伴随着形状的变化，因此被广泛应用于传感器或声波换能器等方面.尤其重要的是，多铁材料不仅可以利用磁电耦合设计磁电变换转换器，而且可以利用电极化和磁极化同时存储数据的多态存储元，可以进行铁电的数据位写入和通过与之关联而产生的磁场读出的新型存储器，还可以用作光开关、光全息存储、传感器等［4-6］.

近期，反铁磁材料ACrO2（A为元素Ag，Cu，Pd，Na）［7-10］由于其螺旋磁序引发铁电性及自旋几何阻挫特征，在实验和理论上均被广泛地报道.结构与ACrO2相似的材料ACrS2却具有很多不同的特性.实验研究表明［11］，当温度降低为47K时，AuCrS2结构由R-3m转变为C2／m，具有共线的双条纹反铁磁基态，其材料没有表现出铁电性.重要的是与材料AuCrS2相比，AgCrS2在48K时［12］，结构由R3m转变为Cm，同样具有双条纹反铁磁基态，并发现材料具有铁电性.目前理论方面缺乏对AuCrS2的系统研究.为了解释该材料无铁电性的原因，对晶体结构和磁性结构更加详细的研究显得尤为重要.本文中根据实验结果，采用基于密度泛函理论的第一性原理，计算了材料的磁基态，磁性作用和电子结构.从理论计算的角度给出了材料磁基态，着重分析了其电子结构导致无铁电性的原因.

1 计算方法

本文中的计算，主要关注AuCrS2在47K温度以下，材料的低温物理特性.本文中采用AuCrS2的实验结构数据［11］，a＝1.444 7nm，b＝0.349 7nm，c＝0.741 9nm，β＝156.454°.我们选用的软件包WIEN2K［13］包含基于密度泛函理论（DFT）的全势线性缀加平面波的第一性原理计算方法（FPLAPW），并采用广义梯度近似（GGA）和电子交换关联函数Perdew-Burke-Ernzerhof（PBE）相结合的方法处理电子间的交换关联势［14］.元素 Au，Cr，S选取的 Muffin-tin分别为2.5、1.9、2.0au.截断参数RMTKmax为7.0，在总的布里渊区内选取100个K点进行计算，能量收敛到1.0×10-4Ry.为反映完整的磁结构，我们采取2×1×1含32个原子的超晶胞.

2 计算结果与讨论

为了研究AuCrS2的基态，考虑到磁性离子Cr3＋的层间和层内的铁磁或反铁磁相互作用的不同，层间有C型磁结构（层间铁磁耦合）和G型磁结构（层间反铁磁耦合），层内有1型磁结构（层内单条纹反铁磁耦合）和2型磁结构（层内双条纹反铁磁耦合），如图1所示.图1中，球的正号表示磁性离子自旋向上，负号表示磁性离子自旋向下，虚线部分为我们选取的超晶胞.

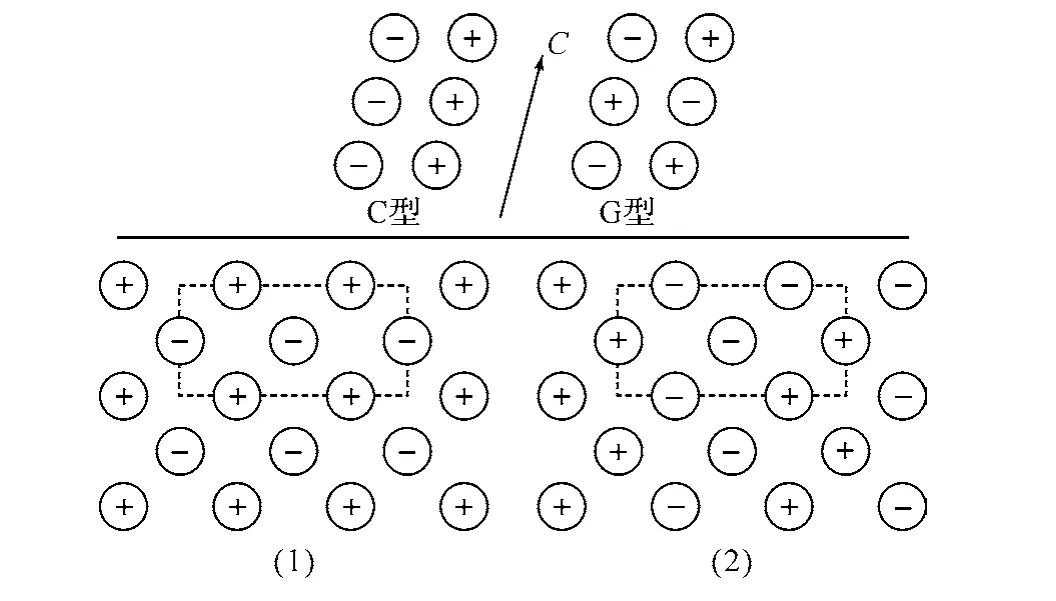
图1 AgCrS2不同的磁结构

AgCrS2不同的磁结构由不同层间磁结构和不同层内磁结构组合而成.我们计算的5种共线的磁结构为：反铁磁态C1（层间铁磁耦合，层内单条纹反铁磁耦合），反铁磁态C2（层间铁磁耦合，层内双条纹反铁磁耦合），反铁磁态G1（层间反铁磁耦合，层内单条纹反铁磁耦合），反铁磁态G2（层间反铁磁耦合，层内双条纹反铁磁耦合），铁磁态FM.通过GGA＋U的自洽计算得出的上述5种不同磁结构的能量、禁带宽度和磁性离子Cr3＋的磁矩，如表1所示.从表1的数据中，可以看出5种不同磁结构的禁带宽度和磁性离子Cr3＋的磁矩基本一致.通过能量的比较，可知反铁磁态G2的能量最低，说明5种不同磁结构中，反铁磁态G2（层间为反铁磁耦合，层内为双条纹反铁磁耦合）的磁结构最稳定，是AuCrS2的磁性基态，此结果与实验结果一致.

表1 计算所得的5种不同磁结构的能量、禁带宽度和离子Cr3＋的磁矩

为了更好地描述磁交换机制，设定磁性离子Cr3＋之间层内最近邻交换常数为J1，层内次近邻交换常数为J2，层内第三近邻交换常数为J3；层间最近邻交换常数为Jc，层间次近邻交换常数为Jc′.磁基态的总能量可以通过海森堡模型近似描述，即：

根据哈密顿量基态的本征能量：H｜0〉＝E0｜0〉，可以计算出交换常数.计算结果如表2所示，值小于零表示铁磁耦合，值大于零表示反铁磁耦合.由表2可看出，J2是铁磁耦合，其他均是反铁磁耦合，这与磁基态是相吻合的.对于AuCrS2，其磁性离子Cr3＋通过CrS6八面体的公共边Cr—Crr进行直接磁交换，通过Cr—S—Cr的90°直角进行间接磁交换.根据GKA（Goodenough-Kanamori-Anderson）经验规则，直接磁交换倾向于反铁磁耦合，间接磁交换倾向于铁磁耦合.由表2还可看出，J3的绝对值最大，这是由于在进行间接磁交换时，短的S—S键长会增强其磁交换作用.最后，由表2可看出，层间交换常数与层内交换常数幅度相似，可知AuCrS2为三维磁结构.

表2 计算所得的各交换常数

与材料AuCrS2相比，AgCrS2在48K时，晶格畸变为Cm，其磁基态同样是层间为反铁磁耦合、层内为双条纹反铁磁耦合的磁结构，并且磁性离子Cr3＋的空间排列与AuCrS2基本相同.在低温下发现AgCrS2具有铁电特性，实验上推测AgCrS2的铁电起因可能是“几何型”铁电.由于实验给出AgCrS2与AuCrS2的晶格参数很接近（AgCrS2：a＝1.378 61nm，b＝0.350 42nm，c＝0.711 32nm，β＝155.276°；AuCrS2：a＝1.444 78nm，b＝0.349 76nm，c＝0.741 97nm，β＝156.454°），考虑到在 BCrS2（B＝Ag，Au）中，铁电性的有无可能与B原子或是S原子有关，我们做了以下测试：在AgCrS2结构（Cm）中，将Ag替换成Au，结构表示为AuCrS2＊（Cm），在晶格常数、原子位置等计算条件不变的情况下做能量计算，与不替换的结构（C2／m）做能量对比，结果如表3所示.

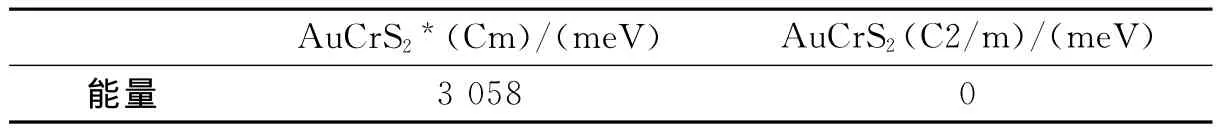
表3 计算所得的2种结构的能量

从表3中可以看出，经过替换原子的结构AuCrS2＊（Cm）能量远比AuCrS2（C2／m）的能量高，说明无铁电性的AuCrS2结构（C2／m）相对稳定.从晶体结构上看，两者Cr原子的空间位置几乎一样，可以判断铁电起源与Cr原子没有关系.不同之处是Au原子和S原子的空间位置.在Cm结构中，Au原子与S原子形成不对称的AuS4四面体结构，不对称结构诱发铁电性；在C2／m结构中，Au原子与S原子形成AuS2对称的线性结构，没有表现出铁电性.通过Cm与C2／m结构相比，可以初步认识到，AuCrS2（C2／m）无磁性的原因是其结构为中心对称结构，而不像AgCrS2（Cm）那样晶格是不对称的而表现出铁电性.

图2（a）为AgCrS2（Cm）的晶体结构图，大球表示Cr原子，次大球表示Ag原子，小球表示S原子；图2（b）为AuCrS2（C2／m）的晶体结构图，大球表示Cr原子，次大球表示Au原子，小球表示S原子.从晶体结构上看，Cr原子的空间位置几乎一样，它与周围的S原子形成CrS6的八面体，表明其基态磁性的一致性.在AgCrS2（Cm）中，Ag原子周围近邻有4个S原子，其中1个Ag—S键长比较短，另外3个键长比较长，形成不对称的AgS4四面体结构；而在AuCrS2（C2／m）中，Au原子周围近邻只有2个S原子，形成对称的AuS2线性结构.

图2 （a）AgCrS2（Cm）的晶体结构；（b）AuCrS2（C2／m）的晶体结构

3 结论

用基于密度泛函理论的全势线性缀加平面波法的第一性原理计算方法，研究了AuCrS2材料的磁学特性和晶体结构特征.理论计算结果表明：AuCrS2结构的基态是层间反铁磁耦合、层内双条纹反铁磁耦合的磁结构，其磁性离子为Cr3＋.对于AuCrS2，其层内Cr离子间的间接磁交换相互作用，对磁结构的形成具有重要作用，且整个晶体表现为三维磁结构.通过Cm与C2／m晶体结构的能量对比，对AuCrS2的无铁电性给予了合理的解释，由于AuCrS2处于基态时，晶体结构中心对称，因而没有表现出铁电性，表明晶格对称性对材料铁电性具有关键作用.

致谢：感谢湖北大学物理学与电子技术学院王卓老师的交流讨论.

［1］Schimid H.Multi-ferroic magnetoelectrics［J］.Ferroelectrics，1994，162（1）：317-338.

［2］Prinz G A.Magnetoelectronics［J］.Science，1998，282（5394）：1660-1663.

［3］Scott J F，Araujo C A.Ferroelectric memories［J］.Science，1989，246（4396）：1400-1405.

［4］Hill N A.Why are there so few magnetic ferroelectrics［J］.J Phys Chem B，2000，104（29）：6694-6709.

［5］Aharonov Y，Casher A.Topological quantum effects for neutral particles［J］.Phys Rev Lett，1994，53：319-321.

［6］Hill N A，Rabe K M.First-principles investigation of ferromagnetism and ferroelectricity in bismuth manganite［J］.Phys Rev B，1999，59：8759-8769.

［7］Ohara Y，Mitsuda S，Yoshizawa H，et al.Magnetic phase transition in AgCrO2［J］.J Phys Soc Jpn，1994，63：847-850.

［8］H Kadowaki，H Kikuchi.Neutron power diffrantion study of the two-dimensional triangular lattice antiferromagnet CuCrO2［J］.J Phys Condens Matter，1990（2）：4485-4488.

［9］Hiroshi T，Hideki Y，Shingo Y，et al.Critical behavior of the metallic triangular-lattice heisenberg antiferromagnet PdCrO2［J］.Phys Rev B，2009，79：104424-104430.

［10］Hsieh D，Qian D，Berger R F，et al.Unconventional spin order in the triangular lattice system NaCrO2：a neutron scattering study［J］.Physica B，2008，403：1341-1343.

［11］Carlsson S J E，Rousse G，Yamada I，et al.Suppression of geometric frustration by magnetoelastic coupling in AuCrS2［J］.Phys Rev B，2011，84：094455-094451.

［12］Damay F，Martin C，V Hardy，et al.Magnetoelastic coupling and unconventional magnetic ordering in the mulitiferroic triangular lattice AgCrS2［J］.Phys Rev B，2011，83：184413-184420.

［13］Blaha P，Schwarz K，Sorantin P，et al.Full-potential，linearized augmented plane wave programs for crystalline systems［J］.Comput Phys Commun，1990，59：399-415.

［14］John P P，Kieron B，Matthias E.Generalized gradient approximation made simple［J］.Phys Rev L，1996，77：3865-3868.