玻璃形成液体其内在结构中的二十面体

李荣娟，孙民华，郑大宇

(1.哈尔滨商业大学能源与建筑工程学院，哈尔滨150076;2.京都大学环境资源工程学院，京都日本6158540;3.哈尔滨师范大学物理与电子工程学院，哈尔滨150025)

玻璃转变液体一直以来都是凝聚态物理研究的重点和难点问题，多年来倍受国内外很多学者的关注[1－6].近年来，人们对于玻璃转变液体的结构理解已经有很大的进步，但关于它的分子构型还没有形成统一定论[7－8].

最近几年，分子动力学(molecular dynamics简称MD)模拟成为研究玻璃转变的一个重要的理论工具.这是由于分子动力学模拟不仅能像实验一样进行各种观察，还可以描述微观的分子运动细节，从而得到材料的结构和性质.

势能曲面(potential energy landscape简称PEL)理论[9－10]是MD模拟中研究玻璃转变行为的一个主要方法[11—15].这是因为 PEL方法能够使玻璃转变液体的分子位置在长时间保持不变，分子就像被冻住一样，从而减少了分析玻璃转变液体结构的难度.PEL是一个复杂的、多维的能量曲面，整个系统中势能大小是根据系统中所有原子构型的变化而定义的[16－17].参考文献[3]给出了 PEL 的图形解释，从他们的图形中我们能看到许多类似盆(basin)的形状，每一个盆中都包含一个能量最小值(局部能量最小值)eIS－L，它对应一个最小的分子构型——内在结构(Inherent Structure简称IS).研究IS的分子构型变化对于理解玻璃转变过程具有十分重要的意义.本文采用分子动力学模拟的方法，利用PEL理论对玻璃形成液体进行研究.同时，对一般液体(typical liquids－没有经过局域能量优化的液体)和IS液体中多面体的分子构型随温度变化情况进行分析.

1 势函数和模拟方法

MD模拟玻璃转变液体，所采用的势函数是Lennard－Jones(L－J)势，L－J势函数的形式为:

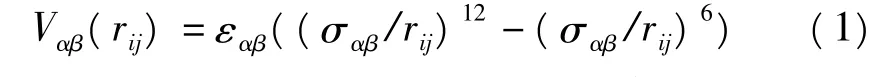
方程(1)中的…α，β∈{A，B}，其中 表示第i(i=1，2，3，...，N)个粒子的位置坐标指的是i原子与j原子之间的距离.参量ε和σ分别为L－J势垒的深度和L－J组元的尺寸.L－J势的参数:εAA=3.984 kJ/mol，σAA=0.341 nm，粒子的质量为m，mA=39.948 amu，并且εAB/εAA=1.5，εBB/εAA=0.5，σAB/σAA=0.8，σAB/σAA=0.88，mB/mA=1，体积 V =(5.5σAA)3[18－20].

本文采用正则系综(NVT)对204个A粒子和52个B粒子组成的二元液体系统进行MD模拟.首先，将这些A和B粒子置于边长为L的立方盒子中.其次，按照周期边界条件，选取的交互截断距离 rc=2.5σA[21]，时间步长选取 0 .000 3 ps.研究的温度范围从600K降到4K，冷却速率为1.3×1012K/s.为了获得IS结构，我们首先应用标准的MD模拟的方法进行高温平衡;然后降温平衡;最后经过瞬时最陡下降(instantaneous steepest descent)的方法[22]使温度迅速的降至2 K，模拟获得IS能量.在每一个温度T下，抽取了25个平衡构型，在这25个平衡构型中选取平均能量值eIS.

2 模拟计算结果及分析

2.1 结构与动力学分析方法

局部方向键体序参数(Local Bond－orientational Order)q6是用来描述原子团簇的几何形状.其定义的形式如下:

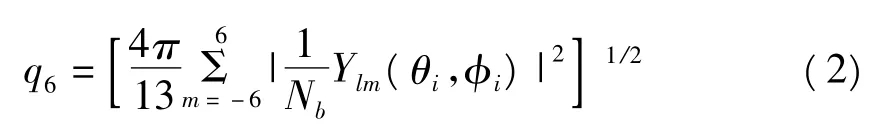
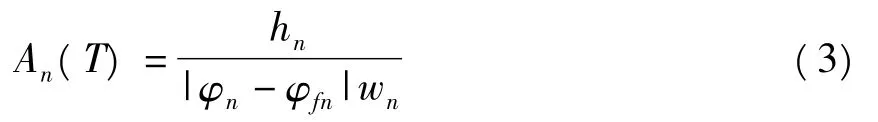
其中:An中的n表示多面体的面，φfn是多面体序的特征角，φn是键角分布函数N(θ)通过高斯拟合第一峰的位置，N(θ)是键角θ概率密度分布，θ是由一个中心原子和两个近邻原子组成的键角，hn是第一峰的高度，wn是高斯拟合第一峰的半高宽.

2.2 结果与讨论

图1显示了玻璃形成液体IS中势能最小eIS随温度的变化关系.从图中我们很容易发现三个明显的分区－平衡态(equilibrium liquid)，过冷态(supercooled liquid)和玻璃态(glass state).当温度高于390 K时，eIS几乎不随温度而变化，此时体系处于平衡态;当温度低于390 K时，eIS随着温度的降低迅速减小，液体系统的动力学开始减慢，此时体

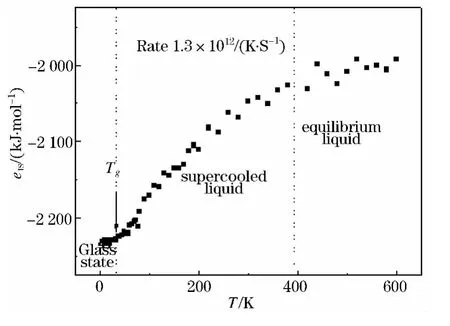
图1 玻璃形成液体IS中势能最小值eIS与温度T的关系

其中:Nb是团簇原子之间的键数，Ylm(θi，i)是球谐函数，θi和φi分别是第i个键的极角和方向角.我们选取的团簇一般是由13个最近邻原子组成.选取方法:把一个原子作为中心原子，然后在它周围找到与中心最近邻的12个原子，这13个原子组成了一个团簇.

M·Sun等人[23]提出了用来描述分子结构堆砌的参数An，An的表达式如下:系跳出了平衡态进入了过冷态;当温度减小到36 K时，随着温度的继续降低eIS值不再有明显的变化，我们把能量开始不再变化这一点定义为玻璃转变点Tg，从Tg=36 K这点开始体系进入了玻璃态.

我们采用局部方向键体序参数q6，对玻璃形成液体分子构型结构进行统计分析.图2描述二元玻璃形成液体系统IS中q6随温度的变化关系，此图与参考文献[23]中的表1对比，发现IS中存在二十面体，六面体和八面体等多面体的结构转变.但是在图2中，很难发现玻璃形成液体系统的具体结构趋向变化.为了更清晰的找到玻璃形成液体组成结构趋向，采用An描述二元液体系统的IS结构趋向.首先计算了IS中多面体序的键角分布函数N(θ)，对于一个13个原子的二十面体团簇，理论上键角分布概率的峰值出现在63.4°，116.4°和180°.图3描述了从24～380 K五个温度下，玻璃形成体系IS中二十面体键角分布函数在各个角度(0°～180°)的百分比.从图2中我们能够观测到N(θ)% 的最大峰值出现在 60°和 110°，而 180°的峰值几乎观测不到，这是因为0°和180°在计算中很难分清，所以我们没有查找180°的键角.63.4°是二十面体中特殊存在的一个角度，因此我们的计算结果能够说明IS结构中存在二十面体序.同时，我们得到的N(θ)%分布与D· Cicco[24]，和 M·Sun[23]所得到的结果相似.从图2中我们还能够观测到，N(θ)%的第一峰的峰值随温度的减小而升高.这表明了当液体系统被冷却时，二十面体序将增多.

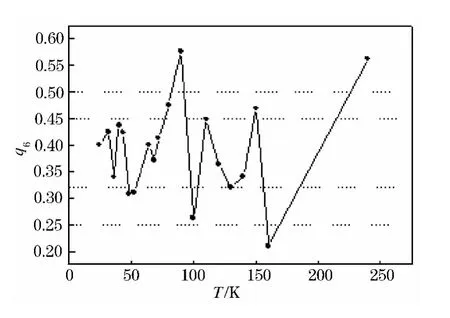
图2 玻璃形成液体IS中的局部方向键序参数(q6)与温度变化关系

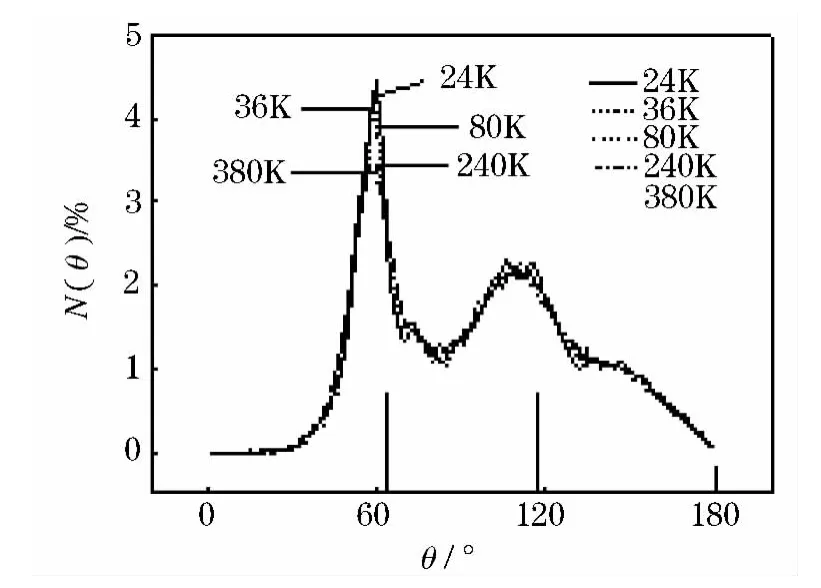
图3 IS中二十面体键角分布概率

图4给出IS中六面体、八面体和二十面体结构的键角分布键序参数An随温度的变化关系，温度的变化范围为380K～24K.从图中可以观察到六面体和八面体序随着温度的降低没有明显变化，而二十面体变化很明显.二十面体随着温度的降低而增加，当温度接近玻璃转变时，二十面体序增长的趋势几乎消失.一般液体中与IS中二十面体相比较，前者比后者的少.根据键角分布键序参数An与温度的变化关系我们能够得出二十面体是形成玻璃转变液体(非晶)的主要结构.玻璃转变不仅是一般液体接近IS的过程，也是二十面体增加的过程.

图4 玻璃形成液体中的六面体、八面体和二十面体结构随温度的变化关系

3 结语

本文对IS中的二十面结构体序进行分析后得出以下结论:二十面体结构随温度降低而稳定增加，当温度下降到玻璃转变温度时，这种增加停止.玻璃转变的IS比一般液体中的二十面体多.玻璃转变过程是一般液体接近IS的过程，同时也是二十面体增加的过程.

[1] WEINTRAUB H，ASHBURNER M，GOODFELLOW P N，et al.Through the glass lightly[J].Science，1995，267(5204):1609－1618.

[2] EDIGER M D，ANGELL C A，NAGEL S R.Supercooled liquids and glasses[J].The Journal of Physical Chemistry，1996，100(31):13200－13212.

[3] DEBENEDETTI P G，STILLINGER F H.Supercooled liquids and the glass transition[J].Nature，2001，410:259 －267.

[4] MAYER P，BISSIG H，BERTHIER L，et al.Heterogeneous dynamics of coarsening systems [J].Physical Review Letters，2004，93(11):115701.

[5] BERTHIER L.Time and length scales in supercooled liquids[J].Physical Review E，2004，69:020201 －020204.

[6] TONINELLI C，WYART M，BERTHIER L，et al.Dynamical susceptibility of glass formers:contrasting the predictons of theoretical scenarios[J].Physical Review E，2005，71(4):041505－041525.

[7] FRECHERO M A，ALARCON L M，SCHULJZ E P，et al.Connections between structural jamming，local metabasin features，and relaxation dynamics in a supercooled glassy liquid [J].Physical Review E，2007，75(1):011502－011508.

[8] SPAEPEN F.Condensed－matter science:Five－fold symmetry in liquids[J].Nature(London)，2000，408:781－782.

[9] GOLDSTEIN M.Viscous Liquids and the Glass Transition:A Potential Energy Barrier Picuture[J].The Journal of Chemical Physics.1969，51(9):3728.

[10] STILLINGER F H，WEBER T A.Packing Structures and Transitions in Liquids and Solids[J].Science，1984，225:983 －989.

[11] BROOKS C L III，ONUCHIC J N，WALES D J.Statistical thermodynamics:Taking a walk on a landscape [J].Science，2001，293:612－613.

[12] SCIORTINO F，KOB W，TARTAGLIA P.Inherent structure entropy of supercooled liquids[J].Physical Review Letters，1999，83(16):3214－3217.

[13] BUCHNER S，HEUER A.Potential energy landscape of a model glass former:Thermodynamics，anharmonicities，and finite size effects[J].Physical Review E，1999，60(6):6507－6518.

[14] SASTRY S.The relationship between fragility，configurational entropy and the potential energy landscape of glass－forming liquids[J].Nature(London)，2001，409:164 －167.

[15] DOLIWA B，HEUER A.Hopping in a supercooled Lennard－Jones liquid:Metabasins，waiting time distribution，and diffusion[J].Physical Review E，2003，67(3):030501 －030504.

[16] STILLINGER F H，WEBER T A.Hidden structure in liquids[J].Physical Review A，1982，25:978 －989.

[17] RANDALL A，VIOLETTE L，STILLINGER F H.Multidimensional geometric aspects of the solid－liquid transition in simple substances[J].The Journal of Chemical Physics，1985，83(8):4079.

[18] KOB W.ANDERSEN H C.Testing mode－coupling theory for a supercooled binary Lennard－Jones mixture I:The van hove correlation function[J].Physical Review E，1995，51:4626 －4641.

[19] KOB W.ANDERSEN H C.Testing mode－coupling theory for a supercooled binary Lennard － Jones mixture.II.Intermediate scattering function and dynamic susceptibility[J].Physical Review E，1995，52:4134－4253.

[20] GLEIMN T，KOB W，BINDER K.How does the relaxation of a supercooled liquid depend on its microscopic dynamics? [J].Physical Review Letters，1998，81(20):4404 －4407.

[21] STODDARD S D，FORD J.Numerical experiments on the stochastic behavior of a Lennard－Jones gas system[J].Physical Review A，1973，8(3):1504－1512.

[22] KOB W，DONATI C，PLIMPTON S J，et al.Dynamical heterogeneities in a supercooled Lennard－Jones liquid[J].Physical Review Letters，1997，79(15):2827 －2830.

[23] SUN M，LI C.A molecular dynamics simulation study of the polyhedral structure of liqud argon during glass transition[J].Modern physics Letters B，2009，23(8):1069－1075.

[24] DI C A，TRAPANANTI A，FAGGIONI S.Is there icosahedral ordering in liquid and undercooled metals[J].Physical Review Letters，2003，91(13):135505－135508.