回转椭球体阻力的数值计算方法研究
王小波, 韩端锋
(1. 航运技术与安全国家重点实验室, 上海 200135; 2. 哈尔滨工程大学, 哈尔滨 150001)
0 引 言
回转椭球体与潜艇主体相似,虽然外形简单,但其绕流场却是一个典型的三维流动实例,对这一流动预报的好坏可以间接地检验数值计算方法对潜艇主体绕流流动的预报能力。因此,作为数学船型的典例,椭球体的基础研究有一定的必要性和重要意义。近年来,椭球体粘性分离流研究受到普遍重视,如国外学者对长细比为6∶1椭球体的粘性绕流进行了实验[1-3]和数值计算研究[4-5],主要集中于湍流模式,对模型前期网格的研究较少;国内对椭球体模型的研究也致力于湍流模型等方向,如李佳等采用不同的湍流模型对某一潜器进行了计算对比,并在入口湍流强度方面做了深入研究,相对而言对网格划分的相关研究较少。
参考相关文献及著作,对回转椭球体粘性三维绕流场进行了数值模拟,集中于绕流阻力的计算;以试验值为参考标准,研究了网格划分对绕流场模拟及计算结果的影响规律。
1 椭球体几何建模及控制域生成
根据试验结果,建立长细比为6∶1的回转椭球体模型,其长半轴a=750 mm,短半轴b=c=125 mm,椭球面通过定轴旋转而成,几何模型见图1。
模拟无界流场中椭球体三维绕流。为消除壁面影响,建立长方体椭球体流场控制域(见图2),采用笛卡尔直角坐标系,椭球体几何中心位于坐标系原点。控制域设定:X向:-5.5L~2.5L,Y向:-2L~2L,Z向与Y向同。其中L为椭球体特征长度,L=1 500 mm。

图1 椭球体几何建模

图2 椭球体几何控制域
2 控制域网格划分
从CFD模拟现状分析,网格质量对CFD计算精度和计算效率有重要影响。以网格形式入手,逐步深入探讨网格数目以及边界层等相关因素对计算结果的影响。
目前,网格形式主要集中为结构化网格和非结构化网格两种。首先应用结构化网格,在椭球体两端采用O型结构化网格形式,这样可极大地提高网格质量,使控制域内网格尤其是近壁面网格不至于出现过小尖角等极限情况,边界层与体网格均为六面体;之后使用非结构化网格,则模型的体网格为四面体单元,边界层为棱锥形的五面体单元。两种网格划分形式分别见图3、图4,非结构化网格模型的表面网格见图5。
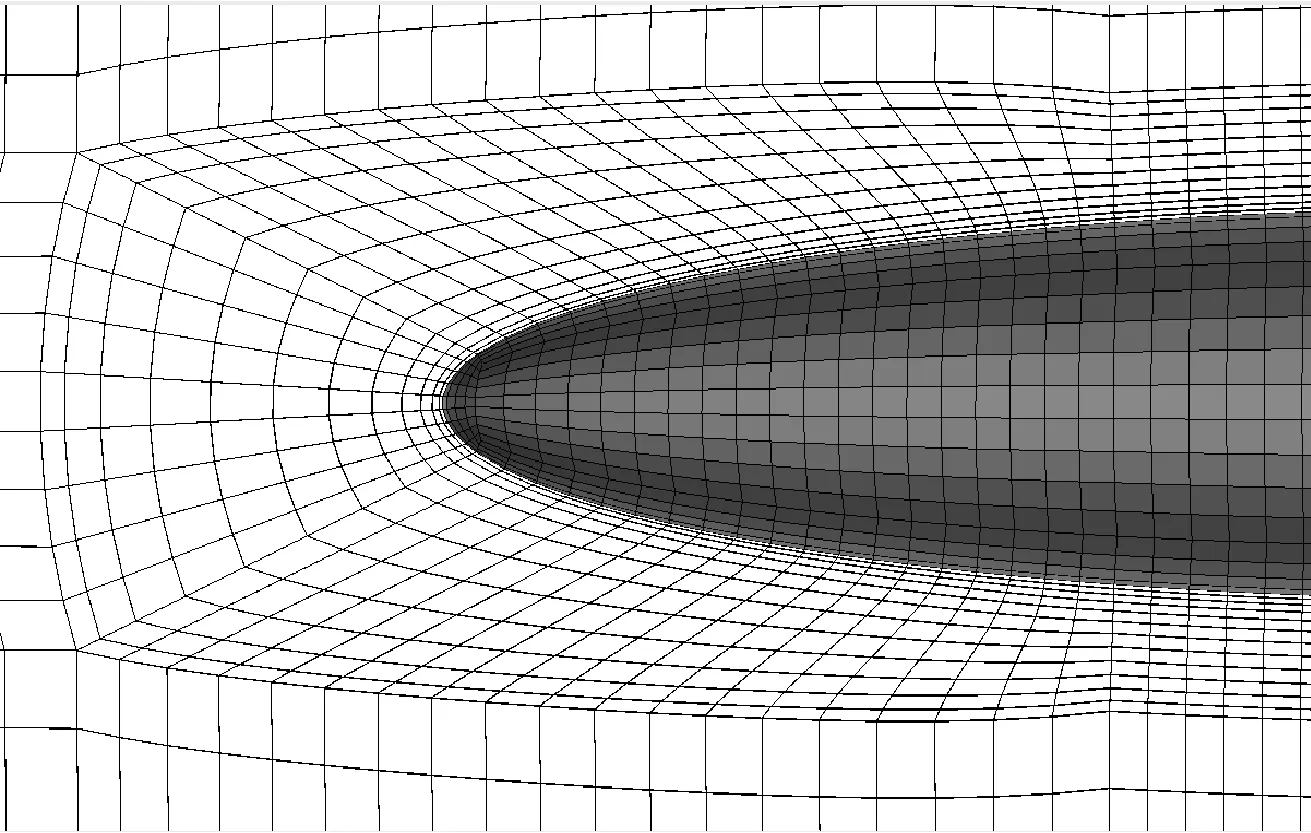
图3 结构化网格及近壁面边界层

图4 非结构化网格及边界层
对边界层网格的设定亦进行了定量研究。不同的边界层数以及底层边界层尺寸的变化都会给计算结果带来一定的波动。根据现有的一些研究成果可知,针对同一网格划分策略,改变边界条件对计算结果精确性的影响相对较大,而改变模型引起的影响则相对较小[8]。在边界层的设置上,近壁面的网格处理采用壁面函数法,根据壁面函数法的要求设定底层网格的尺寸。图6为局部空间网格及边界层网格。

图5 模型表面的非结构网格

图6 结构网格边界层横截面
3 边界条件及求解器参数
欲寻求可靠、高效的数值模拟方法,湍流模型的选取也尤为重要。根据李佳的结论,不同的湍流模型对计算结果会有影响,但是差别不大甚至很小。通过初期计算发现,选取标准k-e湍流模型的阻力计算结果与试验值是非常吻合的。除去网格和湍流模型,入口边界条件以及求解器参数也是影响求解的重要因素。目前针对k-e模型,主要使用的湍流参数有两种:湍动能K和湍动耗散率e,入口湍流强度I和湍动粘度比μt/μ[6]。对于不可压缩外流而言,入口湍流强度的取值并不像内流一样有经验公式可循,只能根据试验值找出一定的规律[9]。入口处湍动能和湍动能耗散率根据经验公式设定:Kin=3.75×10-3U02,εin=K3/2/0.03[10];入口处湍流强度和湍动粘度比根据文献[11]可取I=0.5%,μt/μ=5,变化范围为I=0.1%~0.5%;李佳总结出自由来流湍流强度取值的函数为I=2×107×Re-1.229 8(%)[9]。
经过初步的计算比较,确定的数值方法为:求解器采用分离式求解器,基于有限体积法来离散控制方程;求解稳态三维RANS方程、单相流模型、粘性模型选择标准k-e双方程湍流模型。边界条件:采用速度进口入口条件,出口条件为outflow,物体壁面满足无滑移条件。入口边界条件的湍流参数项为K and Epsilon;压力速度耦合方式为SIMPIEC,压力插值项为PRESTO,对流项及扩散项均采用二阶迎风格式离散。
4 计算结果分析
4.1 网格形式
首先,固定在某一雷诺数下计算,与试验值比较,初步确定适宜的网格形式;在此基础上,通过考察网格数量、边界层网格数以及底层边界层尺寸等参数进一步寻求高精度高效率的网格划分策略;最后,通过改变计算工况验证其准确度。
针对结构化网格和非结构化网格做了大量计算,从中选取了有代表性的五组,同组的网格数相同,而网格形式不同,其余参数均一样,计算结果见图7。
图7中:纵向看,非结构化网格模型的计算值基本上随着网格数量的增加呈减小的趋势,而结构化网格模型的计算值在网格数量多于20万以后变化非常小。横向对比,结构化网格模型的结果普遍低于同组的非结构化网格模型,且更接近于试验值(0.63);在所有的非结构化网格模型中,最好的结果是0.684 5,误差为8.65%。可以说,结构化网格形式整体上更有利于计算结果的收敛和计算精度的提高,因此下面的工作基于结构化网格进行。
4.2 网格数量
由于数值模拟的精度受到网格数量的影响,从常规的角度思考,研究人员往往以增加网格数量的方式保证计算精度。此时,虽然数值模拟不失真,但会增大计算工作量和CPU消耗。在实际操作中,事前并不知道流场的确切情况,因此很难根据流场来建造网格,势必造成网格数量的急剧上升[7]。针对同一流场域,划分了不同网格数量,经过逐一计算,得出了网格数量对计算结果的影响关系。
从实际计算中抽取5个网格数量不同且增量较为均匀的计算模型,对比计算结果,见图8。

图7 两种网格形式的计算结果对比

图8 网格数对结果的影响
由图8可知,各组计算值与试验值较为接近,误差<6%,满足工程精度要求。随着网格数目的增加,计算值小幅度减小,并逐渐靠近试验值。按照此趋势,更多的网格数目将取得更为理想的结果。然而,庞大的网格数量必然耗费大量计算时间,继而影响工作进度,因此,对边界层展开了研究。
4.3 边界层及底层网格尺寸
图9为同一模型在边界层设置不同网格层数时的阻力计算结果,5组网格层数分别为0、6、8、13、25。为考察边界层的必要性,特设定一个无边界层的模型作为比较,其余4组的网格层数逐渐增加,对于回转椭球体,25层的边界层已经足够。
由图9可知,不设置边界层的模型,计算结果与试验值相差较多,这与相关文献的边界层的重要性结论一致。其余4个模型的计算结果较为理想,最大误差为5.2%,最小为2%。
根据覃文洁的研究结论,选取合适的壁面层网格的y+值能够有效提高解的精度;在处理近壁面时采用壁面函数法,壁面层网格的y+值选取的合理性将会影响计算结果的合理性[8]。当然,根据壁面函数法确定的y+有一个取值范围,为寻求更为适宜的近壁面网格尺寸,进行了对比计算,结果见图10。
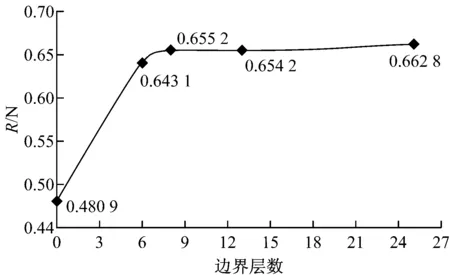
图9 边界层数对计算结果的影响

图10 近壁面底层网格尺寸对计算结果的影响
经壁面函数法确定的底层网格尺寸范围是2.8~14.2 mm。图中给出了五组不同网格尺寸的计算结果,误差最小的是径向尺寸为8.2 mm的模型。另外,超出范围的三组模型计算结果较差,可知底层网格尺寸过小或过大都不利于计算。
经过以上研究,最有利的网格划分策略为:结构网格形式,边界层的网格层数为6层,底层径向尺寸为8.2 mm,满足壁面函数法的要求,总网格数约为7.5万。求解器参数方面,压力速度耦合采用SIMPLEC格式,各方程均采用二阶迎风格式,入口边界的湍流参数为K和E。
4.4 边界条件
入口边界条件的湍流参数尚有多种结论,应用上述研究结论,再考察李佳设定的入口边界条件是否有利于计算。分别赋予湍流强度I以0.1、0.5、1.271 37、5、10,而湍动粘度比恒定为5,计算结果见图11。
由图11可知,随着I的增加,阻力计算值呈上升趋势,并与试验值不断接近,且在I取值为10时,达到较为理想的结果,误差仅为0.59%。而李佳给出的I的经验公式并不完全适用于此计算模型,也反映了CFD的不确定性。
为验证研究成果,对雷诺数为1.42×106(速度为1.0 m/s)及2.13×106(速度为1.5 m/s)都做了数值计算。应用以上结论,使用相同的计算模型、保持统一网格划分策略、微调网格数量以及边界层设置,均取得了较为良好的计算结果,见图12。
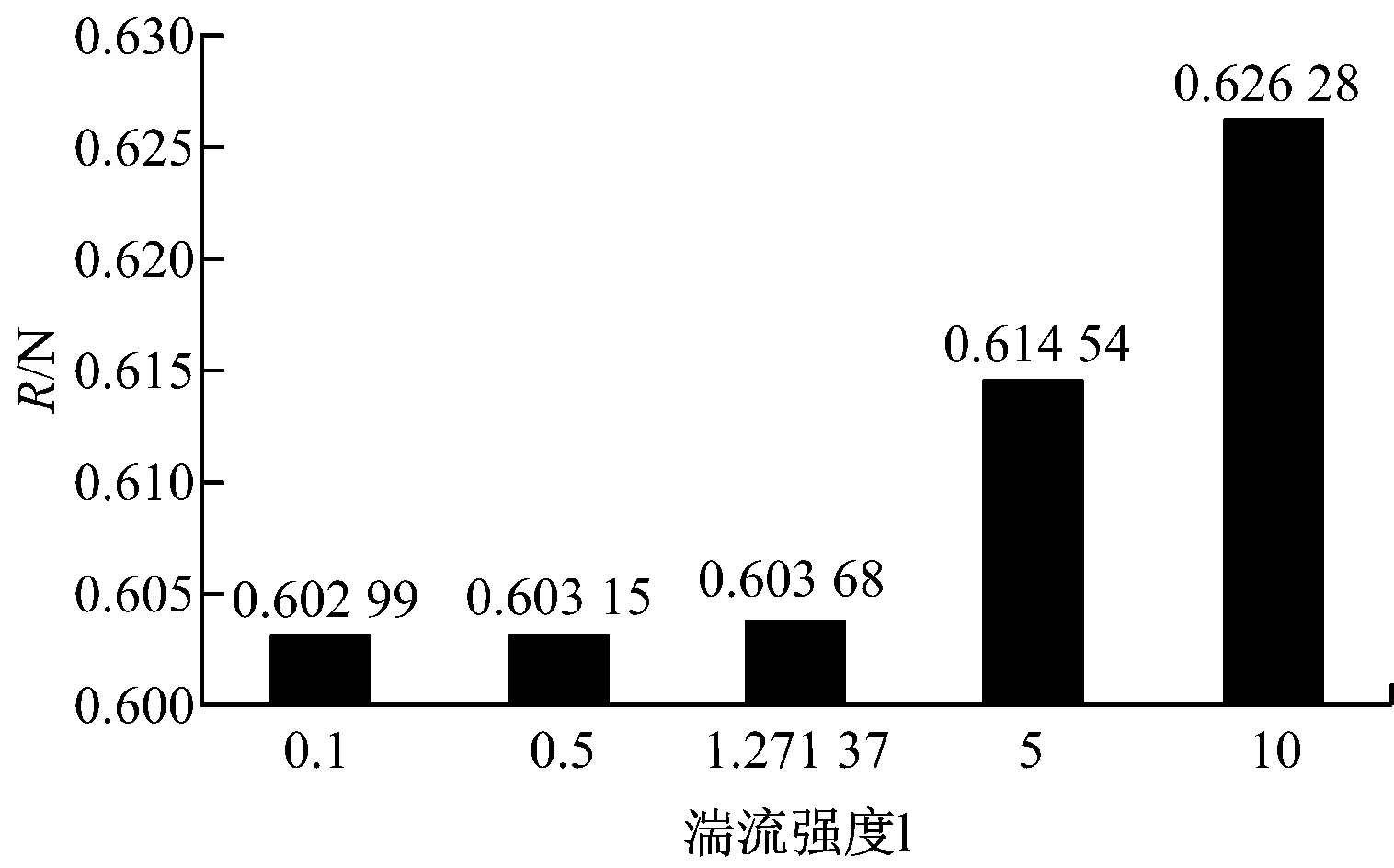
图11 湍流强度对计算结果的影响

图12 不同雷诺数下计算值与试验值的比较
图12中:连接正方块的曲线为试验值,连接菱形的曲线为数值模拟的计算结果。计算值与试验值的吻合程度较好,误差很小,满足工程应用的要求,验证了研究成果的准确性及价值。同时,在这两工况计算中,为了达到更好的计算结果,改变了入口边界条件的湍流参数设定,与速度为0.5 m/s时略有不同。
5 结 语
采用商用CFD分析软件完成了回转椭球体的阻力计算,对其网格划分及网格质量的讨论,可以为复杂模型的网格划分策略提供借鉴。主要集中探讨了几何模型控制域的网格划分对计算结果的影响,包括网格形式、网格数量以及边界层网格划分等,并得出以下结论:
1) 控制域网格划分对计算结果有明显的影响,针对不同的计算模型有不同的网格划分策略,没有通用的一致性原则,但是相近的模型之间可以互相借鉴。
2) 网格数量的增加一定程度上会带来高精度的计算结果,但是庞大的网格数量将给计算机带来过大的负荷从而影响工作效率,并且网格数量增加到一定数量,结果将趋于稳定,变化极小。因此,寻找适宜的网格数量将有助于提高计算精度并减少工作量,这在CFD实际应用中有极为重要的意义。
3) 边界层的存在将极大地提高计算精度,同时近壁面底层网格尺寸在提高计算精度上值得深入探索,目前主要以壁面函数法为参考。
参考文献:
[1] Chesnakas C J, Simpson R L. An investigation of the three-dimensional turbulent flow in the cross-flow separation region of a 6:1 prolate spheroid[J]. Experiments in Fluids, 1994(17):68-74.
[2] Chesnakas C J, Simpson R L. Detailed investigation of the three-dimensional separation about a prolate spheroid[J]. AIAA Journal, 1997,35(6):990-999.
[3] Wetzel T G, Simpson R L. Unsteady three-dimensional cross-flow separation measurements on a pro-late spheroid undergoing time-dependent maneuvers[J].21st Symposium on Naval Hydrodynamics,1997.
[4] Rhee S H, Hino T. Computational investigation of 3D turbulent flow separation around a spheroid using an unstructured grid method[J].Journal of Society of Naval Architects of Japan,2000(18):1-9.
[5] Kim S E, Rhee S H, Cokljat D. High-incidence and dynamic pitch-up maneuvering characteristics of a prolate spheroid-CFD validation[J].24th Symposium on Naval Hydrodynamics,2002.
[6] 王福军.计算流体动力学分析[M].北京:清华大学出版社,2004.
[7] 李刚.潜器水动力特性的数值模拟[D].哈尔滨:哈尔滨工程大学,2011.
[8] 覃文洁,胡春光,郭良平,等. 近壁面网格尺寸对湍流计算的影响[J]. 北京理工大学学报,2006(5):388-392.
[9] 李佳,黄德波,邓锐.载人潜器阻力的数值计算方法分析[J].船舶力学,2010,14(4):334-339.
[10] 邱辽原.潜艇粘性流场的数值模拟及其阻力预报的方法研究[D].武汉:华中科技大学,2006.
[11] 韩占忠,王敬,兰小平.FLUENlL流体工程仿真技术与实例应用[M].北京:北京理工大学出版社,2004.

