基于排队论的高速路机电维护成本模型的建立
王兆刚
(中海网络科技股份有限公司 总经理办公室,上海 200135)
0 前 言
高速公路机电系统组成复杂,技术含量高,并大量使用精密电子元器件,设备运行状况受人为维护效率的影响非常大。如何充分发挥机电设备的作用,推动高速公路营运管理水平不断提高,控制投资方设备维护成本、最大化利用好资源做好高速公路机电维护管理,已经成为摆在面前重要课题。以贵州高速公路机电系统维护为背景,探讨高速路机电系统维护成本的相关因素以及机电系统维护效率与成本因素的关系。同时思考如何利用排队系统服务模型的相关理论来构建机电系统维护成本模型,实现维护资源成本与维护服务水平之间的定量关系的研究。
贵州新思维科技有限责任公司(以下简称“新思维公司”)是贵州省内最大的一家专业机电系统维护公司。目前该公司负责全贵州省约1 700 km、约600个收费车道、约200个收费站、10个路段中心所有相关机电设备及整个供配电和通信网络的维护,该公司目前在贵州省设立了6个维护组。配置的这些资源完全是根据贵州高速公路机电设备使用方(以下称“业主”)委托维护所支付的费用及日常经验来确定资源的数量。目前,由于业主要求提高机电修复的及时性,使得新思维公司人员、车辆、工具等资源的投入势必增加。
提出一种思路,运用排队论相关理论及方法,建立决策模型,针对具体情况,提出相应的解决策略。以便使有限的资源发挥出最大效用,在充分考虑维修效率最大化和成本费用最小化的基础上,取得两者之间平衡。
1 机电设备保养维修成本研究的意义
高速公路机电系统维护费用还缺少全国性的专门统计,但是发达国家制造业的设备维修和养护管理经验可以成为参考。据统计,1986 年英国制造业全年的维修费总额高达11亿英镑,英国全国各行业高达110亿英镑,约占英国国民生产总值的8 %,比英国制造业同年新投资总额的2倍还多。日本钢铁企业的维修费用约占生产成本的12%。德国钢铁企业的维修费用约占生产成本的10%。机电设备和制造业的机械设备相比,全天候工作,外场设备的运行环境恶劣,实际上己达到工业级的苛刻环境。在还贷压力较大的情况下,还不得不支出设备维修养护的费用,这无形中增大了企业运营的成本压力。
从高速公路企业的角度分析,必然把缩短机电系统故障响应时间、缩短故障处理时间、降低解决故障所需成本作为机电系统维护管理的目标。要做好设备维修,必然面临加大人力、维修工具等各方面资源的投入。投入的越多响应的速度越快,成本也相应越高。如何平衡这些关系,根据实际需求制定合理的成本预算,最大化利用维修资源,取得更好的维修效果。从负责机电系统维修的企业的角度分析,在与被服务企业谈判时,如何根据业主的维修响应要求,提出相应的维修报价;或者如何根据被服务企业委托合同金额,确定维护资源的配置规模,以及能够达到的服务级别。
设备维修发生的成本组成从抽象来看,大致可以分为两部分。一是人力成本和材料成本,另一部分则是对磨损的设备零部件需要进行整体和局部更换与修复成本。以贵州省高速公路机电系统维护为背景,研究第一部分维修成本与维修服务响应速度之间的关系。
2 高速公路机电维修过程排队模型
在实际问题中,由于高速公路机电设备发生故障具有很强的随机性,包括地点的随机性、时间的随机性、故障设备的随机性以及维修所用时间的不确定性。在机电设备的维修过程中,考虑一般的情形,利用排队论的思想,将高速公路机电设备故障发生看成排队系统的顾客到达,维修响应时间(包括维修队的行程时间等)与故障维修时间之和视作系统对顾客的服务时间,每个维修队看作1个服务台。将维修队奔赴设备故障发生点进行维修视为对顾客的服务。
这里假设维修队具有完全服务能力:维修队的维修人员应有较丰富的经验和排除或隔离故障的能力;维修队的维修人员专业搭配合理,即保证机电设备各方面出现故障都要有维修人员能够及时的排除。顾客的到达可看做是随机过程,服务时间是相互独立的、服从相同的一般分布的随机变量,且与到达过程也是相互独立的。
2.1 随机服务系统相关定义及系统特征
2.1.1 随机服务系统相关定义
(1) 顾客到来:把机电系统故障看做顾客,把发生每起机电系统故障看做1个顾客的到达,顾客的到达是1个随机过程;
(2) 服务时间(t):指故障排除时间,也就是故障发生后,有空闲的维护队开始对故障进行分析、处理,直到故障解决所需要的时间,t是衡量机电系统维护服务的重要指标和影响维护服务质量的重要因素;

图1 服务时间
(3) 服务台:一组具有基本维修能力的技术人员、维修工具。
2.1.2 随机服务系统的特征描述
发生故障时,当维修队处于空闲状态,对已发生的故障(到达的顾客)立即进行服务。当维修队处于工作状态时,进入排队等待状态,系统实行先到先服务排队规则。该随机服务系统,具有如下特征:
(1) 输入过程:顾客到来的方式为单个,顾客源为无限,顾客相继到达的间隔时间分布特征是随机型的,不同时段的顾客到达相互独立;
(2) 排队规则:按照先到先服务等待规则进行服务,假定系统容量无限;
(3) 服务机构:有多个服务员(维修队),服务方式是对单个顾客进行服务;服务时间也是随机型的,假定服务时间的分布是平稳的,即不受服务时间分布的期望值、方差等参数影响。
2.2 排队系统的主要数量指标
2.2.1 主要数量指标
L为平均队长,即稳态系统任一时刻的所有顾客数的期望值;Lq为平均等待队长,即稳态系统任一时刻等待服务的顾客数的期望值;W为平均逗留时间,即(在任意时刻)进入稳态系统的顾客逗留时间的期望值;Wq为平均等待时间,即(在任意时刻)进入稳态系统的顾客等待时间的期望值。
2.2.2 其他数量指标
s为系统中并联服务台的数目;λ为平均到达率;1/λ为平均到达间隔;μ为平均服务率;1/μ为平均服务时间;N为稳态系统任一时刻的状态(即系统中所有顾客数);U为任一顾客在稳态系统中的逗留时间;Q为任一顾客在稳态系统中的等待时间;Pn=P{N=n}:稳态系统任一时刻状态为n的概率,当n=0时(系统中顾客数为0);P0为稳态系统所有服务台全部空闲的概率;ρ为服务强度,即每个服务台单位时间内的平均服务时间,—般有ρ=λ/(s×μ),当ρ趋近于0时,表明等待时间较短,当ρ趋近于1时,服务台空闲时间较少而顾客等待时间较多。
2.3 维修服务系统模型
由上述随机系统的特征分析,该系统可按照M/M/S队列模型进行建模分析。即维护故障报修的产生符合泊松分布,针对故障的维修服务时间符合指数分布,同时配置了s个维修工作组。
整个系统的平均服务率为sμ,ρ*=λ/sμ,(ρ*<1)为该系统的服务强度。
2.3.1 状态概率
(1)
(2)
2.3.2 主要运行指标
对购电商来说,存在最低收益如果履行合同,购电商从中获取的收益E(Ui)至少不低于最低收益为简化计算,假设
(3)
L=Lq+Sρ*
(4)
(5)
(6)
2.3.3 系统状态N≥S的概率
3 使用EXCEL进行参数计算
1. 计算当前服务组配置进行报修单处理,每个报修单接受服务(含等待)>4 h的概率。
根据新思维现有数据统计,已知参数如下:
1) 平均每小时接到维修单数λ(单位:单数/h)
λ=1.58
2) 平均每个维修单的服务时间1/μ=t
取t=3 h,则μ= 0.33
S= 6
利用EXCEL工具,将模型的相应公式录入见图2。
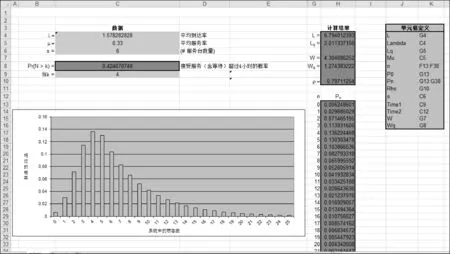
图2 P(N>4)=0.425 1时S值为6
求解得到接受服务(含等待)超过4 h的概率:P(N>4)=0.425 1。即6个维护组,仅能保证4 h维修响应率在57.49%。
2. 假定4 h维修响应率提升至70%以上,计算需要的维护组数量S。
假定4 h维修响应率提升至70%以上,仅改变维护组数量,将EXCEL计算表中的参数s向上调整,看P(N>4)的变化(见图3)。
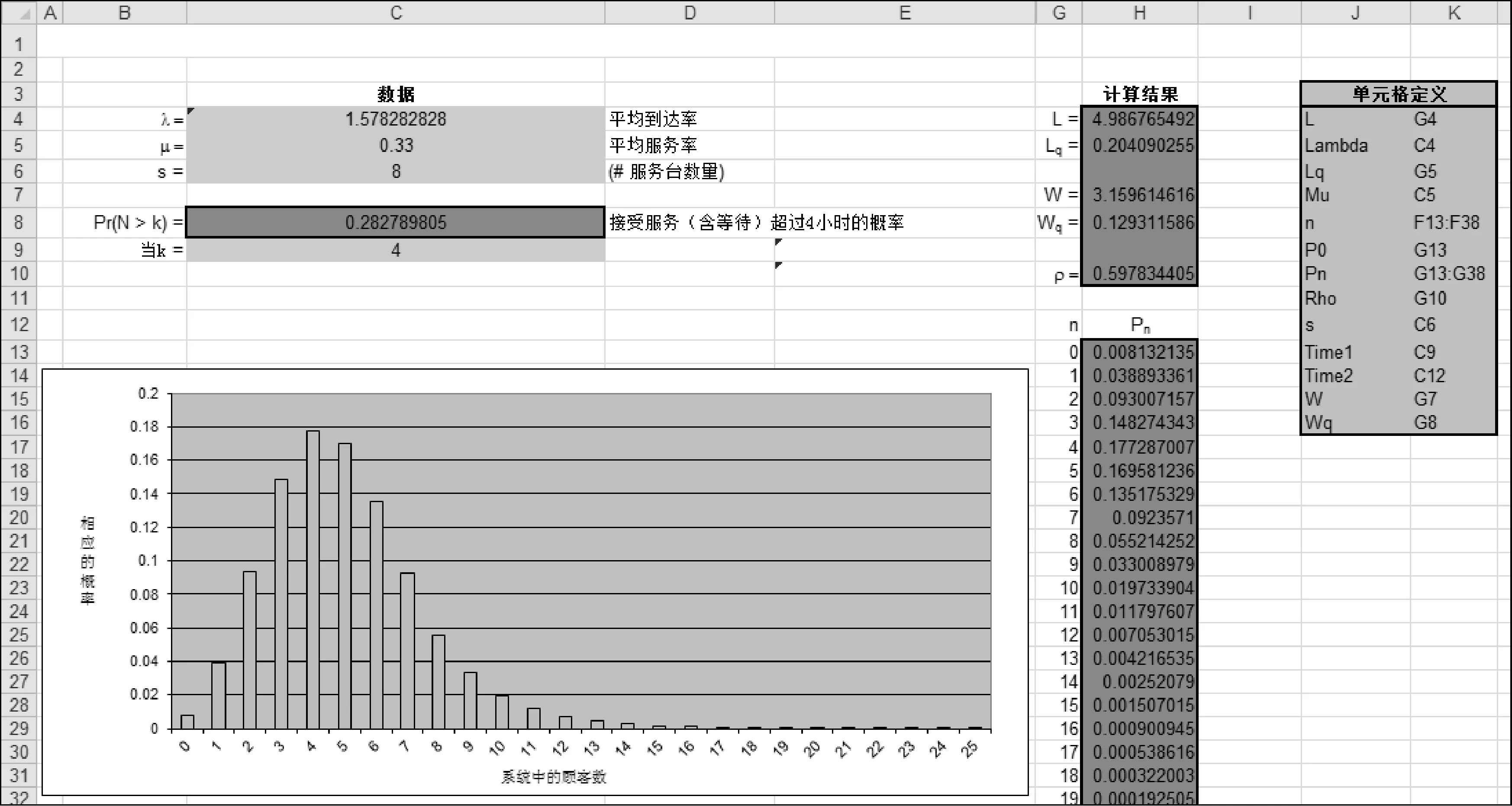
图3 P(N>4)=0.282 8时S值为8
接受服务(含等待)超过4 h的概率:P(N>4)=0.282 8。即至少要保证S=8个维护组,理论上4 h维修响应率在71.72%。
3. 高速公路机电维修成本预算的增加值计算
结合高速公路营运管理单位提出的维修目标,根据排队模型得到的结果,要提升4 h维护响应率,维护组数量需要增加2个。进一步可以得出人员、工具等各类资源的配置数量。根据这些资源的数量,可以生成维修成本预算表。该表可以作为新思维公司与机电运营单位进行维修服务合同定价的重要参考,也可作为公司内部成本控制的重要参考。
新思维公司单个维护组的主要成本由员工工资(含社保、公积金)、制造费用(包括差旅、房租、误餐补助等)、手机通信费、维护消耗材料、车辆维持费、低值易耗品、固定资产折旧、管理费、税金等构成据测算,增加2个维护组年成本预算增加约90万。据此,与业主方进行合同谈判,确定增加成本预算后的合同额,并对维修时效性地提升进行承诺。
4 结 语
应用排队论相关知识,初步研究了高速路机电维修服务水平与维护资源配置成本之间关系。提出以排队论作为决策工具,分析机电设备使用方与机电设备维修方各自关心的两个指标,即维修服务时效性和维修成本支出之间的关系,为决策者提供了一种量化、科学的分析思路。依据该思路及模型,可以将维修实际中的各种数据输入模型中相关参数完成实际的分析工作,有利于维修服务方根据服务目标合理进行相应资源配置和成本测算,同时为双方就维护商务合同进行的谈判提供理论参考。
参考文献:
[1] 叶宗文.维修行业中排队模型的应用[J].四川兵工学报,2009(10):65-67.
[2] 赵建忠,徐廷学,毛旭东,等.M/G/c/∞可修排队系统在航空保障装备数量确定中的应用[J].兵工自动化,2009(10):22-23.
[3] 朱翼隽,鲍媛媛.带有优先权的M/M/N可修排队系统[D].江苏:江苏大学理学院,2007.
[4] 王子刚.电站设备维修决策及优化模型研究[D].北京:华北电力大学,2009.
[5] 徐渝.运筹学[M].陕西:陕西人民出版社,2007.

