圆端形钢管内约束混凝土轴压短柱的力学性能*

付磊 丁发兴 谷利雄 龚永智†

(1.中南大学 土木工程学院，湖南 长沙 410075;2.华南理工大学 土木与交通学院，广东 广州 510640)

当今社会，高速铁路、高速公路快速发展，铁路、公路梁桥工程日益增多.在高烈度地震区，为适应当地地质条件，对桥墩延性有着更高的要求.目前的工程中，多采用圆形或圆端形钢筋混凝土桥墩，其抗震性能较差［1-7］.为提高桥墩的抗震性能，一些实际工程中已开始应用圆端形钢管混凝土(CFRT)轴压短柱［8-11］.CFRT 轴压短柱力学性能的试验与分析结果表明［12］:当钢管宽厚比较大(如宽厚比=5)时，CFRT 的性能近似于钢筋混凝土，钢管不能对混凝土产生有效的约束.有鉴于此，文中提出圆端形钢管内约束混凝土(SCFRT)的概念，即在圆端形钢管内壁焊接拉筋后再浇筑混凝土.它弥补了圆端形钢管约束效果不足的缺陷，使得圆端形钢管内约束混凝土具有接近于圆钢管混凝土(CFT)的高承载力和良好塑性，此外，内部焊接约束钢筋后，可以大大减小钢管壁厚，避免厚钢板焊接时的困难，具有显著的经济效益和良好的应用前景.

为深入了解圆端形钢管内约束混凝土的力学性能，文中基于合理的材料本构关系，采用ABAQUS有限元软件建模分析了圆端形钢管内约束混凝土轴压短柱的几种拉筋内约束形式，并通过试验来验证文中分析方法的合理性.

1 有限元模型

1.1 材料本构关系

以ABAQUS/Standard6.4［13］为工具进行建模，钢材采用等向的弹塑性模型，并且满足Von Mises屈服准则;核心混凝土受到钢管的约束，钢管会对混凝土产生紧箍效应;钢材和核心混凝土的应力-应变关系曲线见文献［12，14-15］.

1.2 单元类型、接触类型及网格划分

为提高计算精度和加快收敛速度，圆端形钢管和混凝土、加载板采用8 节点减缩积分格式的三维实体单元(C3D8R)，对拉钢筋采用两结点线性三维桁架单元(T3D2)，其中加载板采用刚性面以满足计算精度的要求.用结构化网格划分技术划分模型网格，如图1 所示.

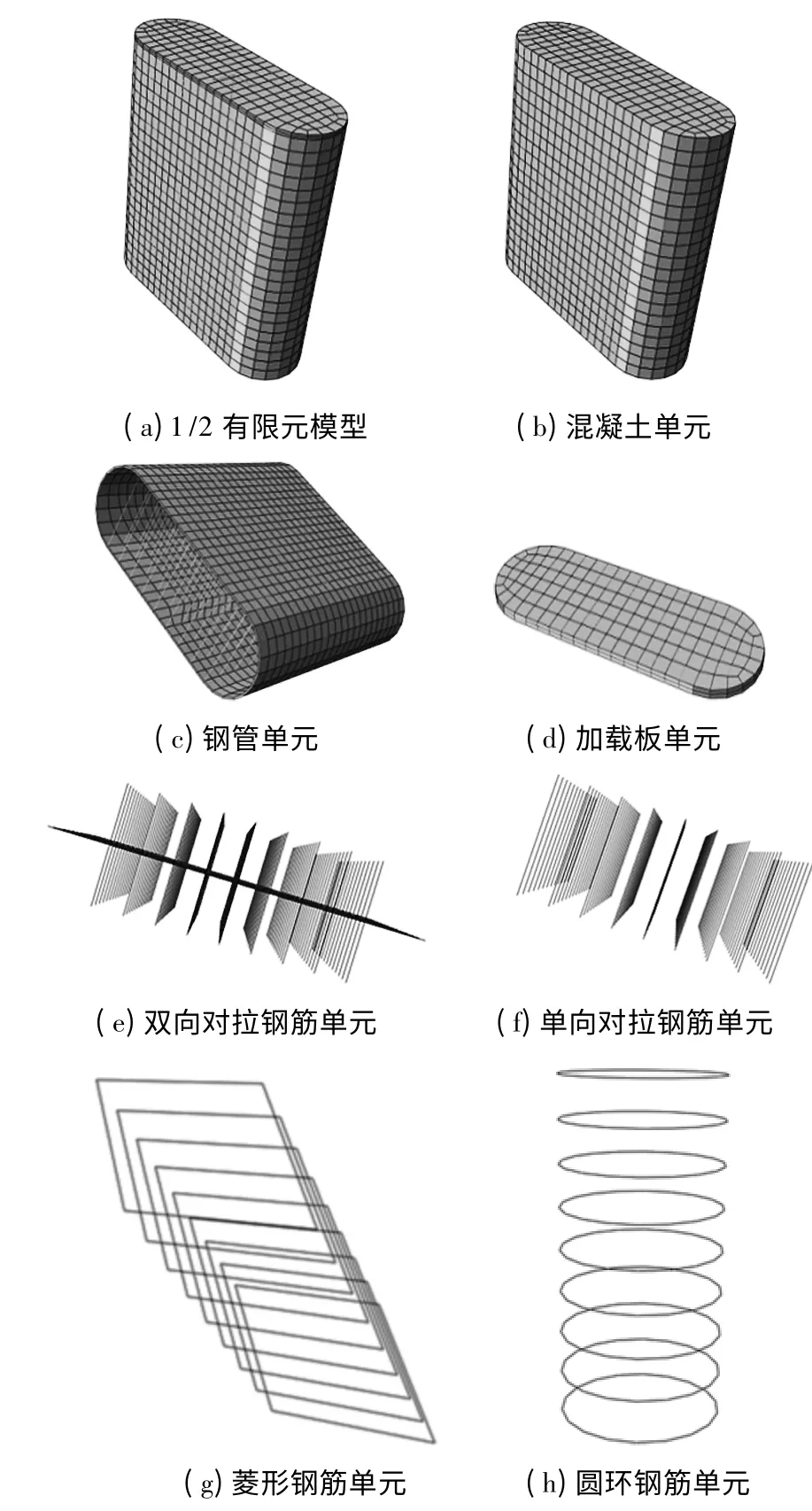
图1 模型网格划分Fig.1 Mesh generation of model

加载板与钢管和核心混凝土采用绑定(Tie)约束形式，钢筋与混凝土采用嵌入形式(Embed).

根据文献［15］，圆端形钢管和核心混凝土的接触关系采用摩擦型，切线方向的接触按照库伦摩擦定义，摩擦系数选为0.5;法线方向的接触按“硬接触”定义，允许钢管和混凝土间有微小的有限滑移.

1.3 边界条件与加载方式

为了节省空间和加快收敛速度，模拟分析时，SCFRT 轴压短柱采用1/2 有限元模型及对称边界条件.为得到曲线的下降段，采用位移加载方式，并采用增量迭代法进行非线性方程组的求解.

2 有限元分析结果

2.1 不同内约束形式的约束效果

圆端形钢管内约束混凝土轴压短柱可能出现的4 种内约束形式分别为:圆环箍筋、菱形箍筋1、菱形箍筋2、对拉钢筋，具体见图2.

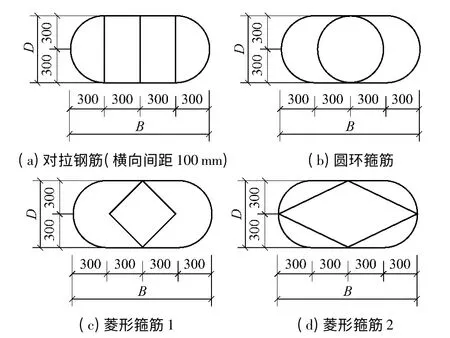
图2 不同内约束形式(单位:mm)Fig.2 Different ways of constraints (Unit:mm)

在保证钢管截面含钢率和拉筋配箍率一致的前提下，选取SCFRT 轴压短柱试件高度L=2400 mm，截面宽度D= 600 mm，截面长度B=1200 mm，混凝土强度fcu=40 MPa，钢管屈服强度fs=345 MPa，钢管厚度t=12 mm，箍筋屈服强度fsv=345 MPa，钢筋沿高度方向间距均为100 mm，计算得到不同内约束形式下的荷载-应变曲线，如图3 所示.由图3 可见，内约束为对拉钢筋的算例试件的承载力最大，延性最好，内约束为圆环箍筋的其次，内约束为菱形箍筋2 的最小.因此，对于圆端形钢管内约束混凝土，建议采用钢筋对拉形式，钢筋与钢管表面焊接牢固.

图3 4 种内约束形式下的荷载-应变曲线Fig.3 Load-strain curves under four constraint forms

2.2 不同钢筋对拉方式的约束效果

根据上述结果，选取对拉钢筋为最佳内约束形式，对SCFRT 轴压短柱中钢筋的不同对拉方式进行参数分析，各种钢筋对拉方式的布置见图4.以钢管为Q235 -Q420，钢筋屈服强度为235～400 MPa，混凝土强度等级为C40 - C100，钢管截面含钢率为0.05、0.10(通过改变钢管壁厚)，宽厚比为2～4 等参数为基础，在保证钢筋沿截面长度、宽度和试件高度方向间距不变的情况下，通过改变钢筋直径分析拉筋配箍率分别为0.005、0.010、0.015、0.020 时双向对拉和单向对拉两种钢筋对拉方式对SCFRT轴压短柱极限承载力的影响.为减少分析量，分析时取Q235 与C40、C60 匹配，Q345 与C60、C80 匹配，Q420 与C80、C100 匹配;取D=600 mm，L=2B，B 分别取1200、1 800 和2 400 mm，t 分别为10.02 与19.38、11.24 与21.62、11.91 与22.89 mm(对应的截面含钢率为0.05 和0.10)，共144 组试件.

图4 双向对拉钢筋的不同布置方式Fig.4 Different arrangements of bidirectional butt joint stirrups

定义Q 为SCFRT 轴压短柱的极限承载力提高系数，其表达式为

式中，Ns和Nw分别为SCFRT 和CFRT 轴压短柱的极限承载力.

SCFRT 柱中拉筋的体积配箍率P 的表达式如下:

式中，n 为每一排对拉钢筋短边方向的个数，m 为试件长度方向的对拉钢筋列数，k 为每一排对拉钢筋长边方向的个数，r 为对拉钢筋半径.

以混凝土强度等级为C40，fsv=400 MPa，fs=235 MPa，t=10.02 mm，D=600 mm，B=1 200 mm，P=0.005，0.010，0.015，0.020 为典型算例，计算得到不同体积配箍率下SCFRT 轴压短柱的极限承载力提高系数随拉筋体积配箍率的变化规律，如图5所示.可看出，当P 大于0.010 时，双向对拉SCFRT轴压短柱的极限承载力要大于单向对拉时;当P 小于0.010 时，双向对拉SCFRT 轴压短柱的极限承载力要小于单向对拉时，可见P=0.010 为单向和双向对拉SCFRT 轴压短柱最佳约束效果的临界配箍率.

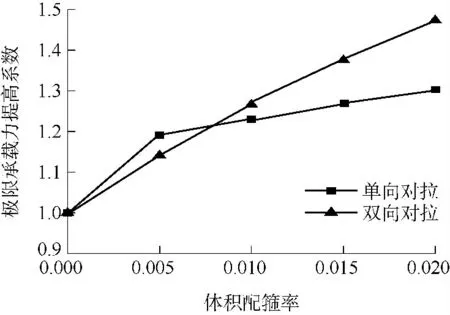
图5 单、双向对拉钢筋的承载力提高系数Fig.5 Improvement coefficient of bearing capacity of singletrack and bidirectional butt joint stirrups

对于圆端形钢管内约束混凝土，提高内约束拉筋的配箍率可增大其极限承载力，因此建议其内约束拉筋的配箍率大于0.010，并采用双向对拉方式.

2.3 双向对拉钢筋内约束方式的优化

为优化对拉钢筋的布置方式，找出最佳对拉约束形式，节省拉筋并达到最佳的受力模式，文中以均匀对拉为基准，在保证体积配箍率一致的情况下，分别考虑双向中间加密对拉、双向均匀加密对拉、双向中间加粗对拉共3 种对拉约束方式对承载力的影响，各种双向对拉约束方式见图4.为与设计试验相对应，选取SCFRT 轴压短柱算例的参数如下:D=600 mm，B=1 200 mm，L=2 400 mm，fcu=40 MPa，fs=345 MPa，t=12 mm，对应的钢管截面含钢率为0.054，fsv=345 MPa，加粗、加密区为截面宽度方向中部300mm范围内，未加密截面横向间距均为300 mm，均匀加密区的横向间距均为100 mm，对应拉筋配箍率为0.081.

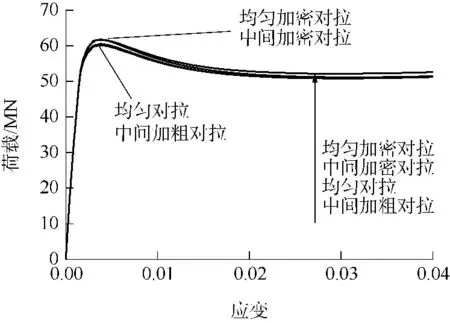
图6 不同双向对拉约束方式的比较Fig.6 Comparison among different constraint ways of bidirectional butt joint stirrups

图6 给出了计算得到的4 种不同双向对拉约束方式的SCFRT 轴压短柱的荷载-应变曲线，可见不同双向对拉约束方式对轴压短柱的极限承载力影响不大，误差均在3%以内，为方便施工，建议采用双向均匀对拉方式的圆端形钢管内约束混凝土.

为探讨双向均匀对拉方式下SCFRT 轴压短柱中钢管和拉筋的受力情况，图7 给出了内约束拉筋和钢管各位置的应力随试件轴向应变的变化情况.

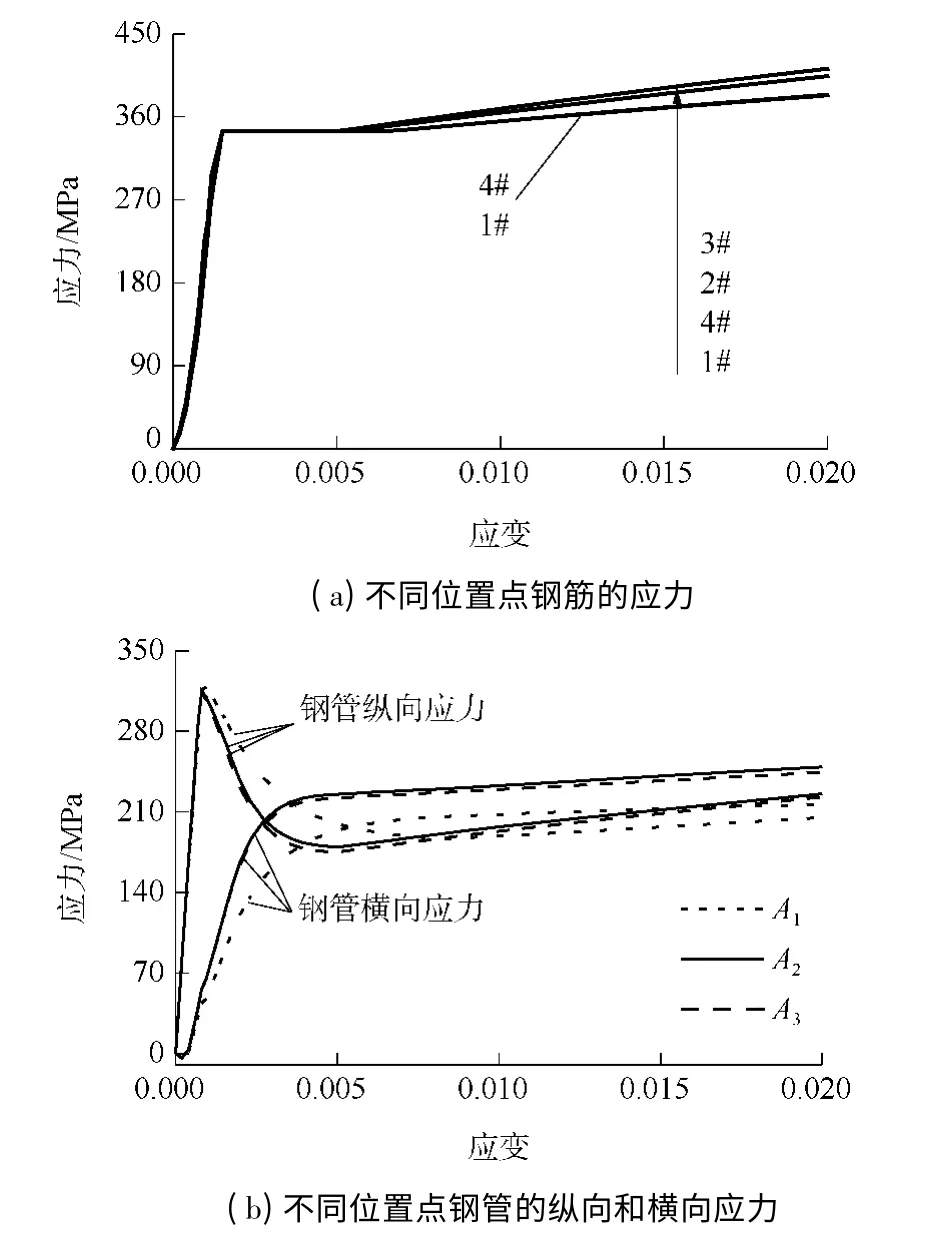
图7 钢管和钢筋各位置的应力变化规律Fig.7 Variation of stress in different positions of steel tube and steel bar

从图7 可看出:①SCFRT 轴压短柱中所有计算点的对拉钢筋全部屈服，3#、2#点的应力较大，4#、1#点的应力相对较小且较为接近，说明沿截面宽度方向的钢筋在靠近试件截面形心位置的约束效应较大，在远离截面形心位置的约束效应略小;沿截面长度方向的钢筋其应力变化规律一致.但由于圆端形钢管约束薄弱处主要位于沿截面宽度方向的中间部位，因此沿截面宽度方向的钢筋应力要大于沿截面长度方向的钢筋应力.②圆端形钢管屈服后，A1、A2和A3点的纵向应力与横向应力相交，A2和A3点的约束效应较强且基本相同，A1点的约束效应相对较弱，说明对拉钢筋后增强了圆端形钢管的约束作用，改变了圆端形截面长度方向中部位置约束较小的受力状况，使得各个位置的约束效应较为均匀，与圆钢管混凝土的约束效应接近.

2.4 相同总含钢率下不同轴压短柱的承载力

在总含钢率(即把圆端形钢管内约束混凝土的对拉钢筋配箍率折算为圆端形钢管混凝土和圆形钢管混凝土的截面含钢率)和混凝土截面面积相同的情况下，进行圆端形钢管内约束混凝土轴压短柱、圆端形钢管混凝土轴压短柱和圆钢管混凝土轴压短柱的承载力分析.总含钢率分别为0.07、0.08、0.10，取圆端形钢管内约束混凝土短柱D=600 mm，B=1200 mm，fcu=40 MPa，fs=345 MPa，t=12 mm，对应钢管截面含钢率为0.06，拉筋屈服强度fsv=345 MPa，箍筋半径分别为7.93、11.29 和15.94mm，横向间距300 mm，轴向间距100 mm，配箍率分别为0.01、0.02、0.04;圆端形钢管混凝土短柱D=600 mm，B=1200 mm，fcu=40 MPa，fs=345 MPa，对应的钢管厚度分别为13.8、15.7 和19.3 mm;圆钢管混凝土短柱fs=345 MPa，钢管的外直径分别为935.90、940.26 和948.92 mm，钢管的厚度分别为15.57、17.75 和22.08 mm.

相同总含钢率和混凝土截面面积下，SCFRT 轴压短柱极限承载力(N2)、CFRT 轴压短柱极限承载力(N1)和CFT 轴压短柱极限承载力(N3)的比较见表1，不同总含钢率下3 种轴压短柱的荷载-应变关系的有限元计算结果见图8.在总含钢率相同的情况下，圆形钢管混凝土轴压短柱的承载力最大，约束效果最好;圆端形钢管混凝土轴压短柱的承载力最小，约束效果最差.此外，总含钢率较高时，圆端形钢管内约束混凝土的约束效果更强，延性改善更明显，说明圆端形钢管内约束混凝土方案是可行的.

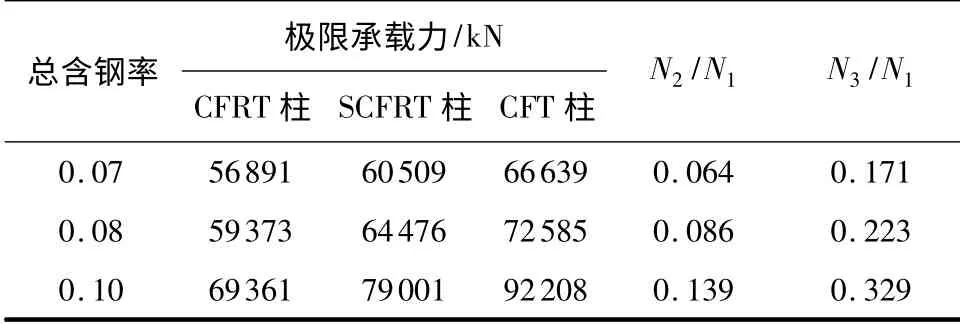
表1 相同总含钢率下3 种短柱的极限承载力Table 1 Ultimate bearing capacity of three short columns under the same steel ratio

图8 不同总含钢率下3 种短柱荷载-应变关系的计算结果Fig.8 Calculated results of load-strain relations of three short columns under different steel ratios

2.5 双向均匀对拉方式下SCFRT 轴压短柱的试验验证

为验证SCFRT 轴压短柱有限元分析的合理性，对2 根双向均匀对拉方式的SCFRT 轴压短柱和2 根CFRT 轴压短柱进行试验研究，各试件实测尺寸见表2，对拉钢筋沿截面长度方向的间距见图9，对拉钢筋沿试件高度方向的间距S 均为50 mm.其中实测钢管屈服强度为311 MPa，极限强度为460 MPa;φ6 mm拉筋的屈服强度为435 MPa，极限强度为615 MPa;试件实测混凝土立方体抗压强度为35.5 MPa.

表2 各实测试件的特性参数Table 2 Characteristic parameters of tested specimens

测试时，在每个SCFRT 轴压短柱试件的钢管中部截面处布置3 个应变花，其位置对应于图9 中的C1、C2和C3，另一相对面布置2 个位移计，其位置对应于图9 中的C1.轴压试验在中南大学高速铁路建造技术国家工程实验室5000 kN 静力实验系统上进行.位移计安放位置如图10 所示，试验采用分级加载模式:弹性阶段每级荷载约为极限荷载的10%，弹塑性阶段每级荷载约为极限荷载的5%;每级荷载持续加载3～5 min 后采集一次数据，试件接近其极限荷载后连续采集数据.

图9 SCFRT 轴压短柱钢管截面(单位:mm)Fig.9 Section of SCFRT stub columns (Unit:mm)

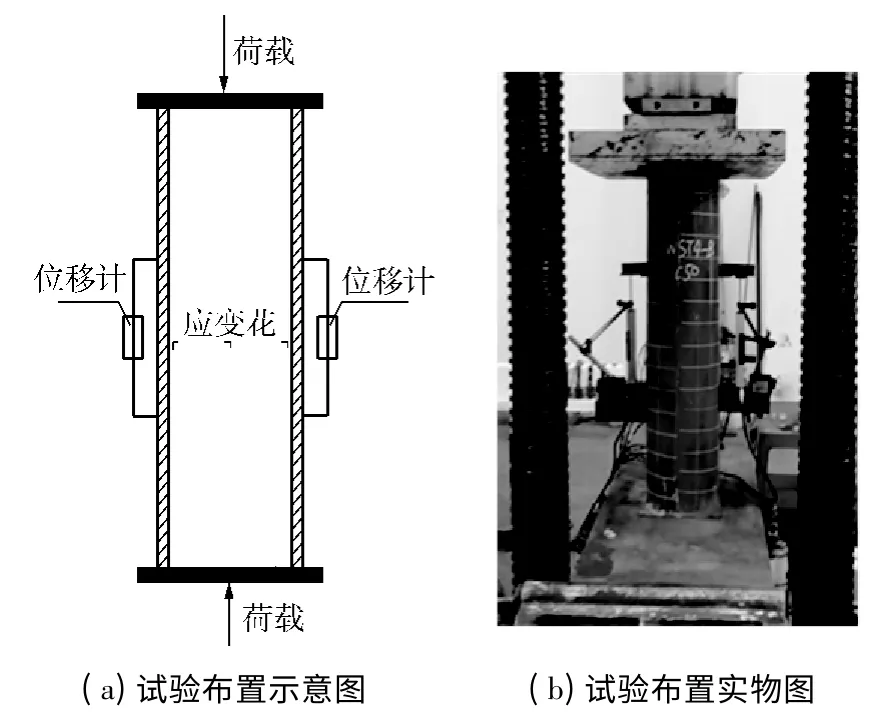
图10 试件试验布置图Fig.10 Test arrangement of specimens

采用ABAQUS 非线性有限元软件计算得到的CFRT 轴压短柱和SCFRT 轴压短柱的极限承载力计算结果(为依据两个试件实测尺寸的平均值所建立模型的计算结果)与试验结果的比较，以及有限元计算得到的试件破坏时钢管表面屈曲的最大幅值Au见表2，试件试验和模拟的破坏形态如图11所示，可见带拉筋约束后圆端形钢管内约束混凝土短柱延缓了圆端形钢管混凝土短柱的局部屈曲现象.

采用ABAQUS 非线性有限元软件计算得到的CFRT 轴压短柱和SCFRT 轴压短柱的荷载–应变有限元曲线与试验曲线的比较如图12 所示，两者的极限承载力吻合良好.

图11 试件破坏形态Fig.11 Failure modes of columns

图12 试件荷载-应变曲线比较Fig.12 Comparison of load-strain curves of specimens

有限元计算得到的典型试件破坏时中部截面的应力云图如图13 所示，圆端形钢管混凝土轴压短柱的非约束区面积(图形核心区域)明显大于圆端形钢管内约束混凝土轴压短柱的非约束区面积，说明焊接对拉钢筋后加强了对核心混凝土的约束.

图13 典型试件破坏时的截面应力云图Fig.13 Section stress nephograms of typical specimens

3 结论

文中通过对圆端形钢管内约束混凝土轴压短柱力学性能的仿真及试验分析，得到以下结论:

(1)SCFRT 轴压短柱的4 种内约束形式(对拉钢筋、圆环箍筋、菱形箍筋1、菱形箍筋2)中，对拉钢筋的内约束效果最好.

(2)在钢筋屈服强度大于外围钢管屈服强度、拉筋体积配筋率大于0.010 时，双向对拉SCFRT 轴压短柱的极限承载力要好于单向对拉时，且随着配筋率的增大短柱的极限承载力增幅变大.

(3)双向对拉钢筋的布置方式对SCFRT 轴压短柱的承载力影响不明显，实际工程应用中建议采用双向均匀对拉钢筋布置的圆端形钢管内约束混凝土，并采用高强度拉筋，且拉筋体积配筋率宜大于0.010.

(4)双向均匀对拉方式的SCFRT 轴压短柱的试验结果和有限元计算结果吻合良好，说明双向均匀对拉约束方式是合理的.

［1］叶献国，王海波，孙利民，等.钢筋混凝土桥墩抗震耗能能力的试验研究［J］.合肥工业大学学报:自然科学版，2005，28(9):1171-1177.Ye Xian-guo，Wang Hai-bo，Sun Li-min，et al.Experimental research on seismic energy dissipation performance of reinforced concrete bridge pier［J］.Journal of Hefei University of Technology:Natural Science，2005，28(9):1171-1177.

［2］蒋丽忠，邵光强，姜静静，等.高速铁路圆端形实体桥墩抗震性能试验研究［J］.土木工程学报，2013，46(3):86-95.Jiang Li-zhong，Shao Guang-qiang，Jiang Jing-jing，et al.Experimental study on seismic performance of solid piers with round ended cross-section in high-speed railway［J］.China Civil Engineering Journal，2013，46(3):86-95.

［3］鞠彦忠，阎贵平，刘林.低配筋大比例尺圆端型桥墩抗震性能的试验研究［J］.土木工程学报，2003，36(11):65-69.Ju Yan-zhong，Yan Gui-ping，Liu Lin.Experimental study on seismic behaviors of large-scale RC round-ended piers with low reinforcement ratio［J］.China Civil Engineering Journal，2003，36(11):65-69.

［4］司炳君，李宏男，王东升，等.基于位移设计的钢筋混泥土桥墩抗震性能试验研究(I):拟静力试验［J］.地震工程与工程震动，2008，28(1):123-129.Si Bing-jun，Li Hong-nan，Wang Dong-sheng，et al.Experimental evaluation of seismic performance of reinforced concrete bridge piers designed on the basis of displacement(I):quasi-static test［J］.Journal of Earthquake Engineer and Engineer Vibration，2008，28(1):123-129.

［5］刘鸣，陆本燕，刘伯权.钢筋混凝土桥墩破坏模式识别方法［J］.中国公路学报，2011，24(3):58-63.Liu Ming，Lu Ben-yan，Liu Bo-quan.Failure mode identification method of reinforced concrete bridge pier ［J］.China Journal of Highway and Transport，2011，24(3):58-63.

［6］尚维波，张春宁.高墩刚构桥系梁抗震分析［J］.长安大学学报:自然科学版，2012，32(1):62-65.Shang Wei-bo，Zhang Chun-ning.Seismic analysis of tie beam of rigid frame bridge with high pier［J］.Journal of Chang'an University:Natural Science Edition，2012，32(1):62-65.

［7］梁启智，汤海波.普通钢筋混凝土连续梁抗震性能的有限元分析［J］.华南理工大学学报:自然科学版，1995，23(1):1-11.Liang Qi-zhi，Tang Hai-bo.Analysis of anti-seismic behavior of the reinforced concrete lintel beam by finite element method ［J］.Journal of South China University of Technology:Natural Science，1995，23(1):1-11.

［8］李彬，李新，周丹，等.圆端形钢管混凝土双肢塔柱受力性能试验研究［J］.建材世界，2009，30(3):31-33.Li Bin，Li Xin，Zhou Dan，et al.Analysis of mechanical properties of round-end concrete filled steel tubes coupled column［J］.The World of Building Materials，2009，30(3):31-33.

［9］蔡崇华，谢建雄，卢哲安，等.微膨胀圆端形钢管混凝土力学性能研究［J］.建材世界，2009，30(2):31-33.Cai Chong-hua，Xie Jian-xiong，Lu Zhe-an，et al.Study on the mechanical properties of micro-expansive circle-end concrete filled steel ［J］.The World of Building Materials，2009，30(2):31-33.

［10］谢建雄，蔡崇华，卢哲安，等.微膨胀圆端形钢管混凝土双肢柱试验研究与数值模拟［J］.武汉大学学报:工学版，2010，43(4):485-489.Xie Jian-xiong，Cai Chong-hua，Lu Zhe-an，et al.Test study and numerical simulation of micro-expansive round-end concrete filled steel tubes coupled column［J］.Engineering Journal of Wuhan University:2010，43(4):485-489.

［11］易贤仁，李彬，卢哲安，等.圆端形钢管微膨胀混凝土塔柱非线性接触分析［J］.混凝土，2010，243(1):33-36.Yi Xian-ren，Li Bin，Lu Zhe-an，et al.Nonlinear contact analysis on round-end micro-expansive concrete filled steel tubes tower-column［J］.Concrete，2010，243(1):33-36.

［12］谷利雄，丁发兴，付磊，等.圆端形钢管混凝土轴压短柱受力性能研究［J］.中国公路学报，2014，27(1):123-129.Gu Li-xiong，Ding Fa-xing，Fu Lei，et al.Mechanical behavior of concrete-filled round-end steel tubular stub columns under axial load［J］.China Journal of Highway and Transport，2014，27(1):123-129.

［13］Hibbitt，Karlson，Sorenson.ABAQUS version 6.4:theory manual，users’manual，verification manual and example problems manual［M］.Hibbitt:Sorenson Inc，2003.

［14］Ding Fa-xing，Ying Xiao-yong，Zhou Lin-chao，et al.Unified calculation method and its application in determining the uniaxial mechanical properties of concrete［J］.Frontiers of Architecture and Civil Engineering in China，2011，5(3):381-393.

［15］丁发兴，李刚，龚永智，等.钢骨-圆钢管混凝土轴压短柱力学性能分析［J］.中南大学学报:自然科学版，2012，34(9):3625-3630.Ding Fa-xing，Li Gang，Gong Yong-zhi，et al.Behavior of tubular stub columns of axially loaded steel-reinforced concrete-filled circular steel［J］.Journal of Central South Unversity:Science and Technology，2012，34(9):3625-3630.