结构可靠性优化设计的证据理论和微分演化方法＊

唐和生，苏 瑜，薛松涛，邓立新

（1.同济大学 结构工程与防灾研究所，上海 200092；2.同济大学 土木工程防灾国家重点实验室，上海 200092）

基于可靠性的优化设计是不确定性结构优化设计的有效途径.传统的可靠性优化设计常采用概率模型，但概率方法需要足够的统计数据信息来拟合其概率特征，而实际工程中这些数据通常是无法准确获知的，所以传统概率方法面临巨大的挑战.

近年来，国内外很多学者致力于发展非概率的不确定建模手段，并在其基础上提出非概率可靠性优化设计方法，其中由 Dempster[1]和Shafer[2]提出的证据理论具有较强的不确定处理能力，已经成为不确定信息表达和量化的有力工具，在多目标识别、信息融合、多属性决策等领域获得了广泛应用[3－6].而基于证据理论的工程可靠性优化分析刚刚起步，并且主要应用于机械与航空领域.Mourelatos等[7]将证据理论应用于内压容器可靠性优化设计中，研究了基于证据理论的失效概率或可靠度指标的计算问题.Bae等[8]运用证据理论解决机械工程中的不确定问题，实现了飞机机翼结构的可靠性优化设计.郭慧昕等[9－11]提出了证据理论和区间分析相结合的可靠度优化设计方法，将此应用于内压容器和气门弹簧的可靠性研究中.尽管已经取得了一些进展，但是证据理论仍然很少应用于实际工程的可靠性优化问题中，计算成本是导致该问题的主要原因.同时，基于证据理论的可靠性优化设计在土木工程中的应用还是一个新课题.

为此，本文采用证据理论处理不确定情况，引入微分演化算法降低证据理论在可靠性优化中的计算成本，提出了证据理论和微分演化算法相结合的可靠性优化设计方法，并将该方法应用于桁架结构的形状优化问题中，来验证本文所提方法的有效性.

1 证据理论的基本原理

证据理论是由Dempster和Shafer提出的，又称为D－S理论.它是建立在辨识框架上的一种不确定理论，设Θ为辨识框架，它表示关于命题互不相容的所有可能答案的有限集合，类似于概率论中有限的样本空间，幂集2Θ定义为辨识框架Θ中所有子集的集合，证据理论是对幂集元素进行基本概率赋值[12].定义函数m：2Θ→[0，1]，∀A⊆Θ.当满足：

称m为框架Θ上的基本信任分配函数（BBA），m（A）为A的基本信任度，表示证据对A的信任程度，若m（A）＞0，则称A为焦元.

若m为框架Θ上的基本信任分配函数，则称由

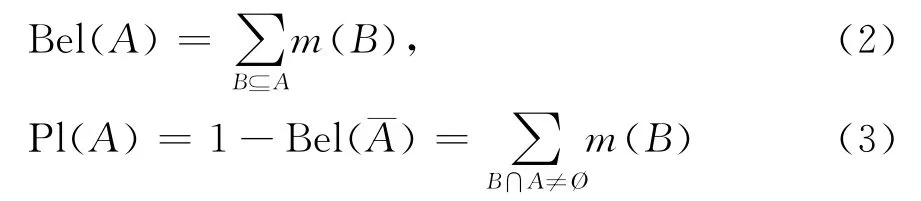
所定义的函数Bel：2Θ→[0，1]为Θ上的信任函数，函数Pl：2Θ→[0，1]为Θ上的似然函数，Bel（A）表示对A为真的信任程度，Pl（A）表示对A为非假的信任程度，也称为命题A的似然度，两者之间的关系如图1所示，Bel（A）和Pl（A）提供了概率P（A）的上限和下限.由此可见，以概率论为基础的传统可靠性问题只是证据理论的一个特例.

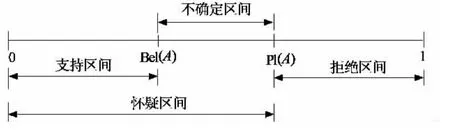
图1 对命题A的不确定描述Fig.1 Uncertainty representation of proposition A

对于认识不够透彻的不确定参数，可能会有多个专家提出不同的理论或不同的数据来组成多源证据，证据理论可以通过合成规则综合考虑各种证据源的影响.经典的D－S合成规则为：假定m1和m2是同一辨识框架Θ上的2个基本信任分配函数，焦元分别为Ai和Bj，则新的基本信任分配函数m为：

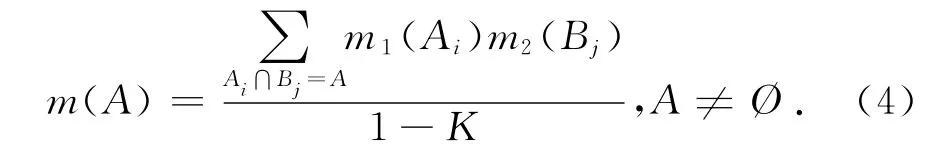
2 证据理论和微分演化算法相结合的可靠性优化设计方法

2.1 基于证据理论的可靠性优化设计模型

一般来说，基于概率理论的可靠性优化问题可表述为：

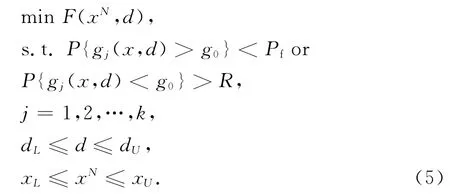
式中：x＝[x1，x2，…，xn]T为n维不确定性量，分别服从一定的概率分布，[xL，xU]为不确定量x的名义值xN的取值区间；d＝[d1，d2，…，dm]T为m维确定性量，[dL，dU]为d的取值区间；F和g分别为目标函数和约束函数；g（x，d）＞g0表示结构发生失效，g（x，d）＜g0表示结构安全，g0为许可的响应值；k为约束条件的数目；P｛｝表示真实概率；Pf和R分别为结构设计给定的失效概率和可靠度许用值.

当问题中不确定量的认识信息较少或不完整时，上述优化模型中的约束条件不能采用概率理论来建立，此时，可以利用证据理论的不确定建模手段解决这一问题.如图1所示，证据理论用似然函数和信任函数来进行不确定性度量，可以证明[Bel，Pl]是真实概率的区间估计，真实的失效概率或可靠度夹逼在该区间内：

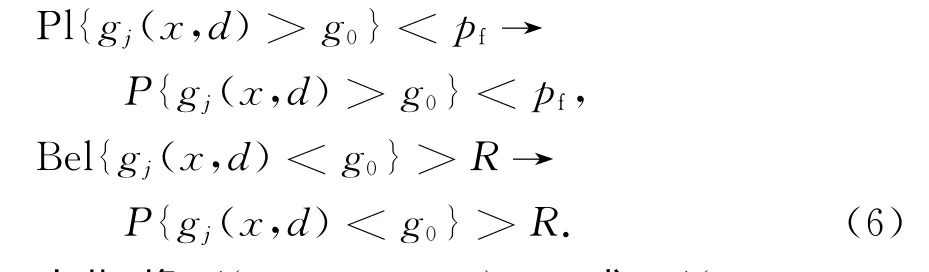
由此，将Pl｛gj（x，d）＞g0｝＜pf或Bel｛gj（x，d）＜g0｝＞R作为传统可靠性约束条件的替代模型，建立基于证据理论的广义可靠度优化设计数学模型：

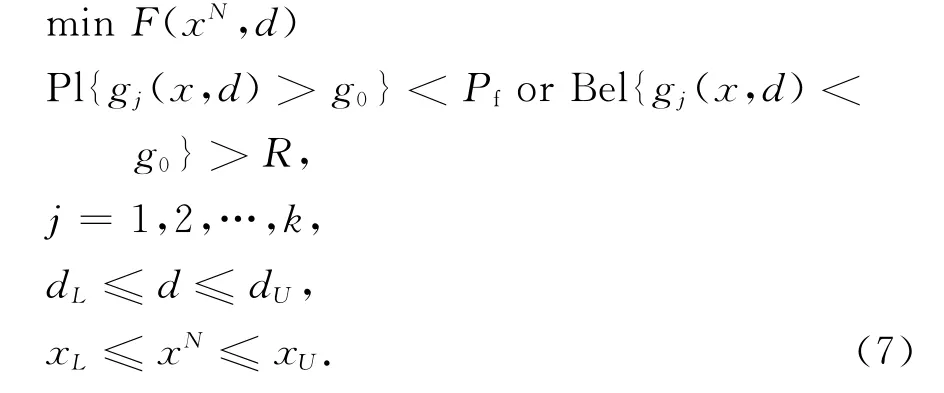
模型中Pl｛gj（x，d）＞g0｝或Bel｛gj（x，d）＜g0｝是进行非概率可靠性分析的前提，由于结构失效占整个设计空间的比例较小，故以Pl｛gj（x，d）＞g0｝＜pf作为约束条件可以提高优化效率，下面就Pl｛gj（x，d）＞g0｝的计算进行详细阐述.

2.2 基于微分演化方法的失效似然度计算

对于结构分析中出现的不确定量，证据理论将其表述为区间数.在计算结构失效似然度时，首先根据不确定量的可能取值范围，将其划分为有限个互不相容的基本区间作为辨识框架.以图2为例，不确定量x1的辨识框架X1＝｛x11，x12，x13｝，幂集2X1＝｛Ф，｛x11｝，｛x12｝，｛x13｝，｛x11，x12｝，｛x11，x13｝，｛x12，x13｝，X1｝，基于证据（专家意见或实测数据）分析，对幂集中的焦元进行基本信任度赋值，得到x1的基本信任分配函数m.

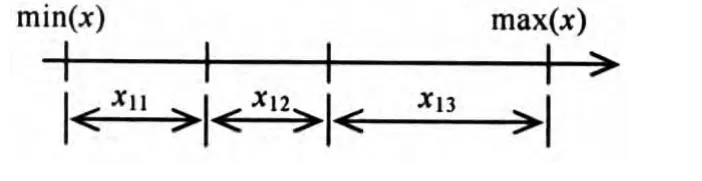
图2 不确定参数基本区间Fig.2 Basic intervals of uncertainty parameter

然后，对每个不确定变量的焦元进行笛卡尔运算，得到联合焦元区间，以二维不确定参数为例：

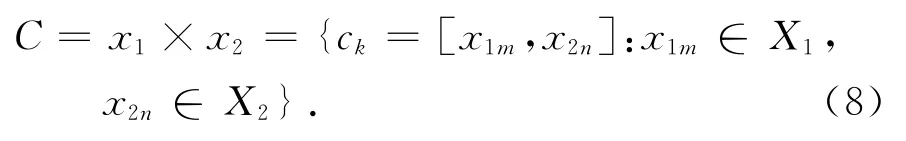
式中：x1m，x2n和ck分别为X1，X2和C的焦元区间.考虑到x1和x2的独立性，二维联合焦元的基本信任度m（ck）＝m（x1m）m（x2n）.

由于x1m和x2n都是区间，焦元ck在集合上为一矩形，显然，对于n维问题，联合辨识框架中的焦元为n维“超立方体”.令y（x，d）表示结构极限状态函数，结构失效域F为：

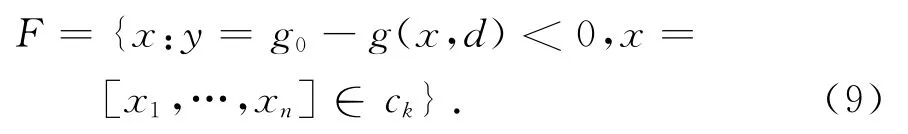
在联合BBA和失效域F的基础上，可根据式（2）和式（3）计算结构失效测度Bel（F）和Pl（F）为：

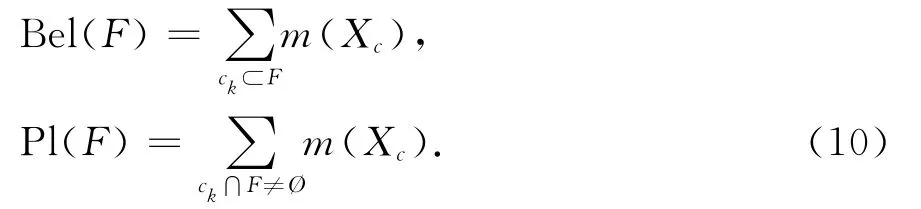
可见，在计算失效测度时需要确定联合焦元ck是否满足ck⊂F或ck∩F≠Ø，图3描述了ck对Bel（F）和Pl（F）的贡献.从图3可以看出：1）若ymax＞0，ymin＞0，则ck∩F＝Ø，ck对Pl（F）和Bel（F）没有贡献，即ck不参与Pl（F）和Bel（F）的计算.2）若ymax＜0，ymin＜0，则ck∩F＝ck，ck对Pl（F）和Bel（F）的计算都有贡献.3）若ymax＞0，ymin＜0，ck仅对Pl（F）有贡献.

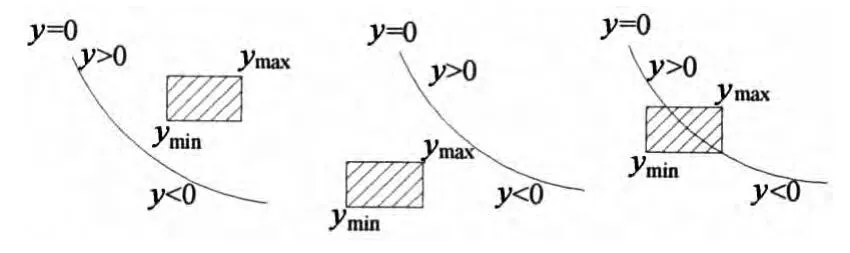
图3 焦元区间对失效似然度的贡献Fig.3 Focal element contribution to plausibility of the failure region

因此，为准确判断，需要求解y（x，d）在ck对应的“超立方体”域上的极值，即

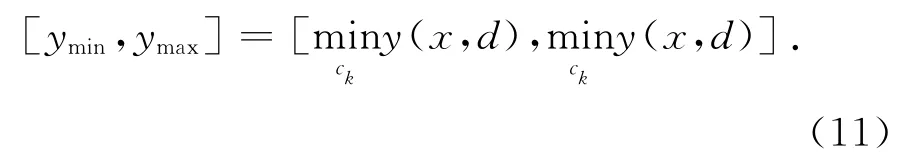
求解式（11）中区间极值的主要方法有采样法和优化方法，采样法的精度很大程度上取决于采样点数目，计算代价巨大.优化方法会极大降低计算量，但由于不确定量x的焦元区间数目多，而且结构响应并不是简单的显式而是通过有限元分析得到的，故利用传统的优化算法求解复杂多维非凸的极限状态函数y（x，d）在ck上的极值显得非常困难.

近年来仿生智能优化算法被广泛引入到结构优化中，例如模拟退火法（SA）[14]、遗传算法（GA）[15]、微分演化法（DE）[16]等，其中DE是一种新颖的启发式智能算法，采用变异、交叉和选择3项基本操作，通过若干代种群演化操作不断舍弃劣质解，保留优质解，最终获取近似全局最优解.研究表明，微分演化算法在求解非凸、多峰、非线性优化问题中表现出较强的稳健性，同时具有收敛较快的优点[17].因此，本文采用DE提高y（x，d）区间极值的求解速度，如图4所示，从而减少优化设计的计算成本.

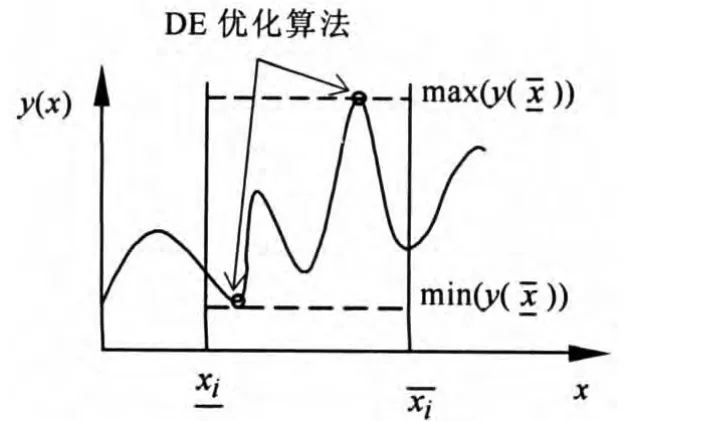
图4 区间函数极值求解Fig.4 Interval optimization for computing bounds

根据以上描述，基于证据理论的可靠性优化设计是利用微分演化算法在满足可靠性约束Pl｛g（x，d）＞g0｝＜pf的条件下，寻求结构最优设计变量和最优目标值.同时，基于证据理论的结构约束失效似然度又是通过微分演化算法来提高其计算效率的，可靠性约束条件的计算流程如图5所示.

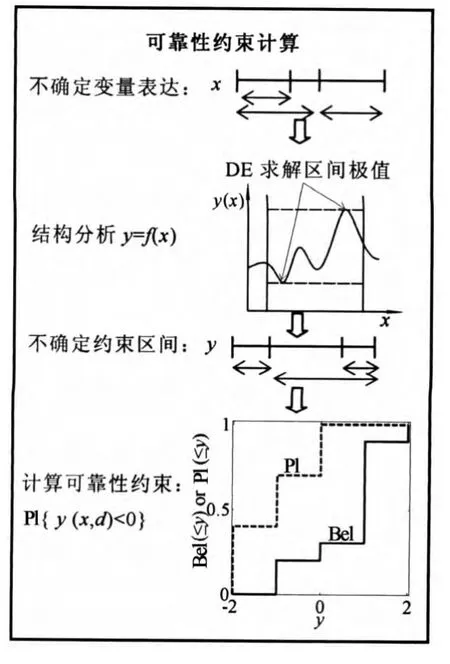
图5 可靠性约束计算流程Fig.5 Flowchart of calculation of reliability constraint

3 算例分析

为了便于比较，取文献[18]中的25杆桁架形状优化进行讨论，结构形式见图6，弹性模量名义值E＝68 950MPa，作用于桁架上的荷载名义值列于表1，容许拉压应力[σ]＝±275.6MPa，各节点三向允许的最大位移为8.89mm.其他参数见文献[18].

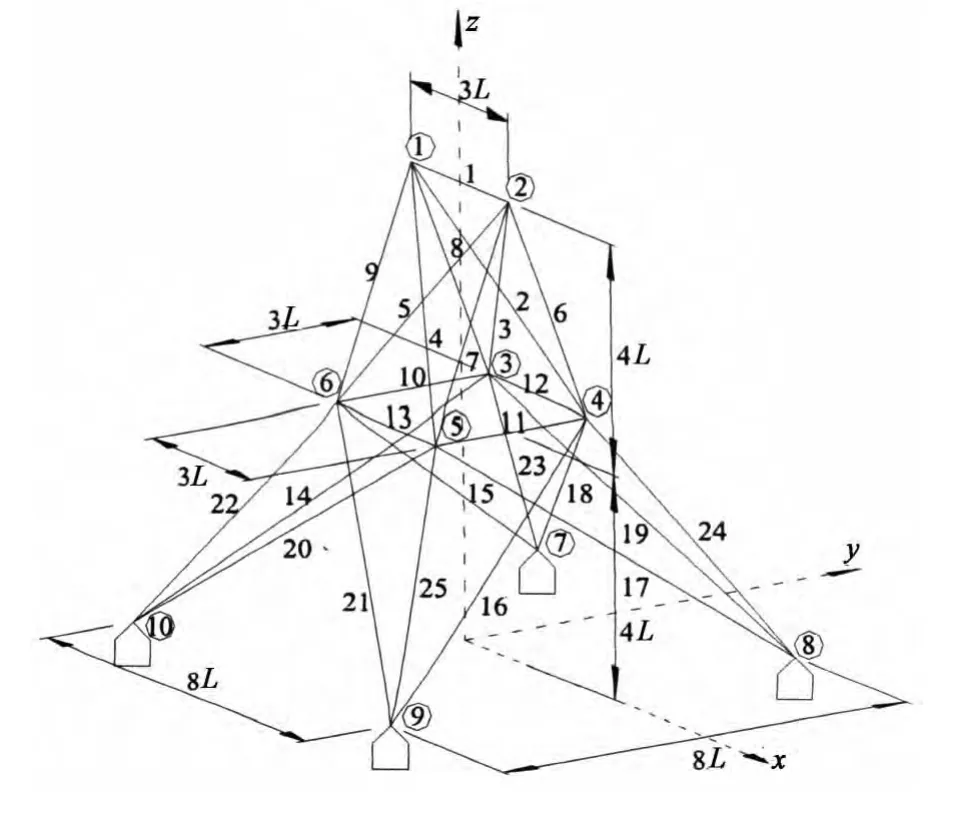
图6 25杆空间桁架结构Fig.6 25bar space truss structure

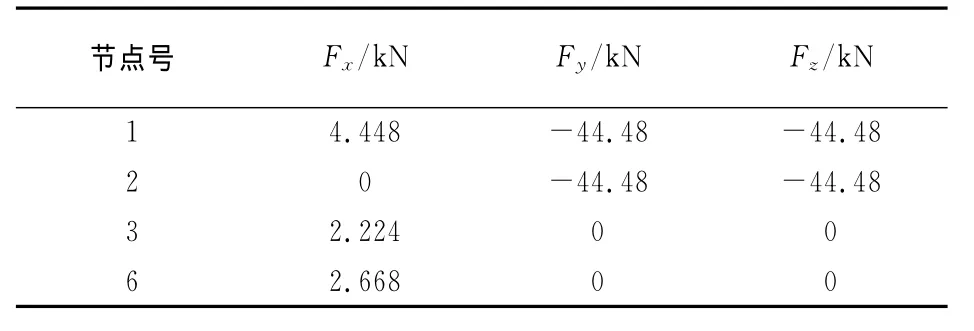
表1 25杆桁架节点荷载名义值Tab.1 Normal value of joint load for 25－bar truss

文献[18]对该桁架进行了确定性优化，本文在此基础上考虑不确定情况，将外荷载和弹性模量视为不确定的，假定其不确定信息（焦元区间及基本信任度）如表2所示，在2种不确定因素存在的情况下，进行既满足可靠度约束条件又使结构总质量最小的最优设计，该不确定优化问题的数学模型为：

式中：d为尺寸和形状设计变量；x为不确定参数；Pl｛gi（x，d）＜0｝＜Pf为约束条件；g1和g2分别表示应力和位移极限状态函数；σk为第k组杆件的应力值；ujl为特定节点j在给定方向l上的位移值.

考虑结构允许的失效概率Pf为0.05和0.1二种情况，采用本文所提方法对25杆桁架进行可靠性形状优化.Pf＝0.05情况的评价函数收敛曲线和最终形状分别见图7和图8.图9给出最优设计时位移约束函数g2（x，d）的信任度和似然度累计分布曲线.为了与文献[18]的确定性形状优化结果相比较，根据图9，表3详细列出了应力和位移约束失效似然度.

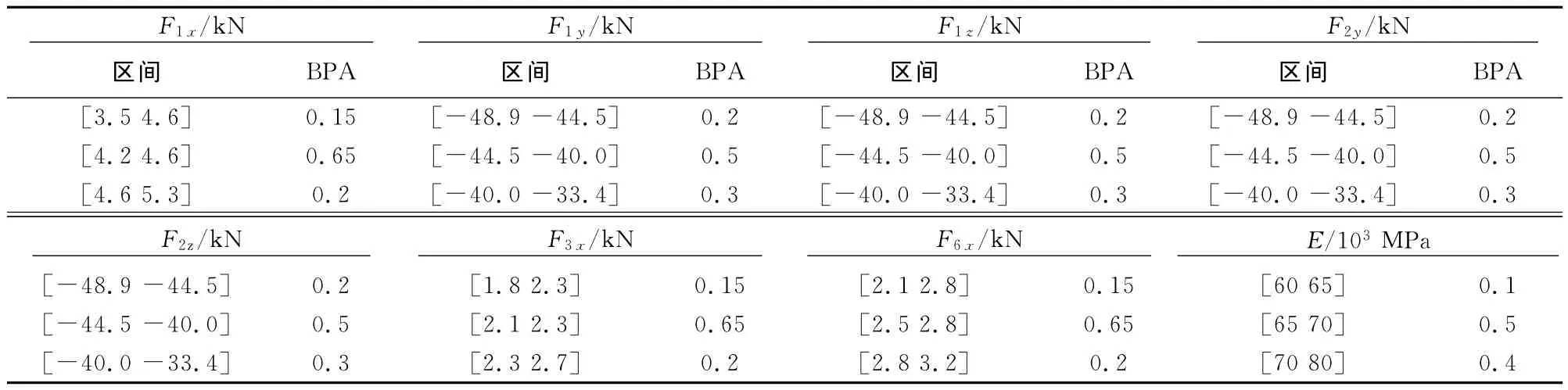
表2 外荷载和弹性模量的不确定信息Tab.2 The uncertain information of load and elastic modulus

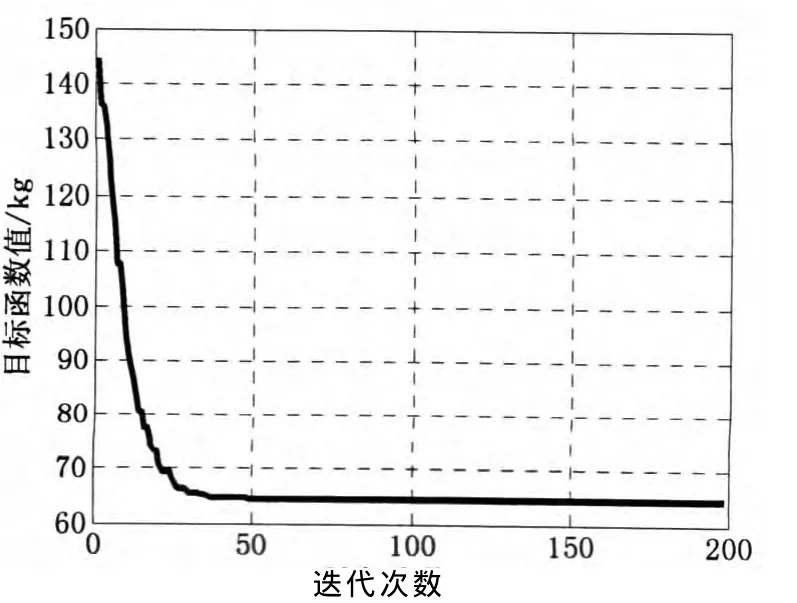
图7 25杆桁架形状优化的收敛曲线Fig.7 Shape optimization convergence history of 25－bar truss

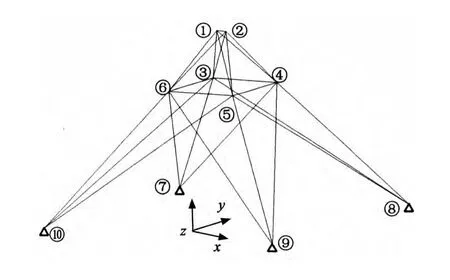
图8 25杆桁架的形状优化结果Fig.8 Optimum shape of 25－bar truss

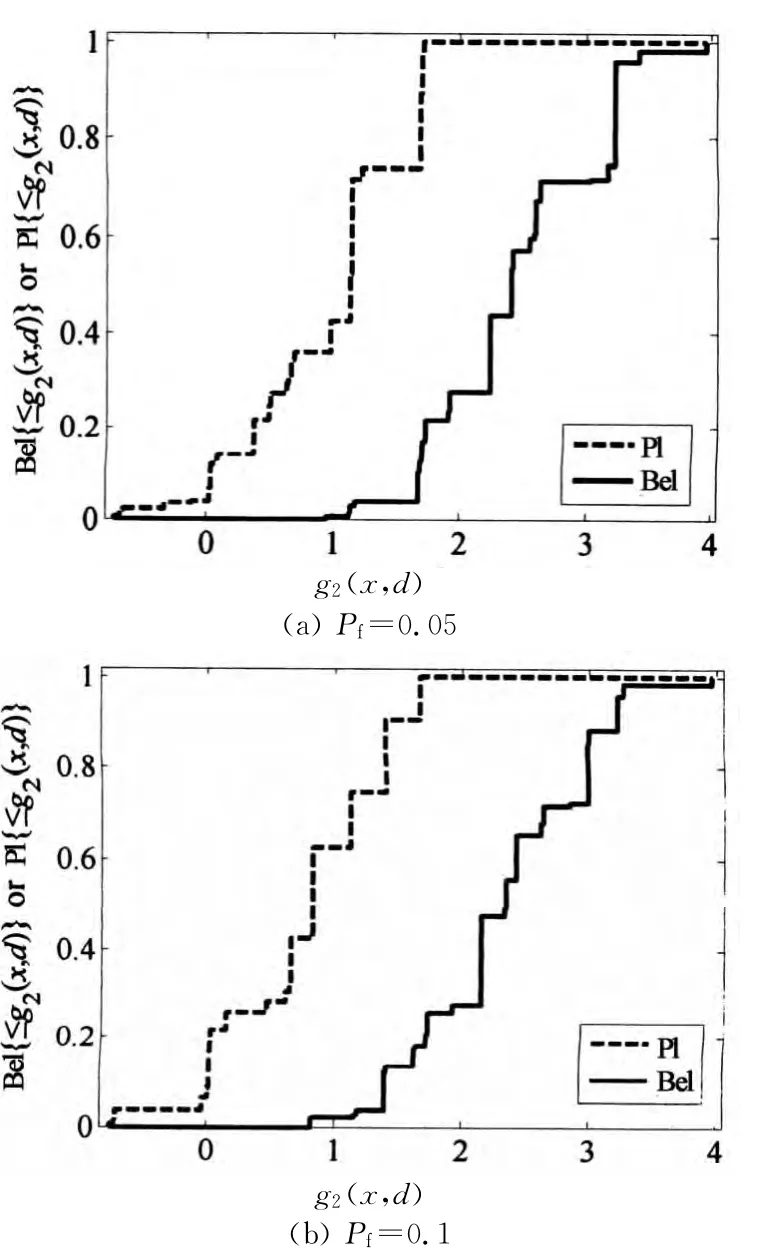
图9 位移约束的信任度和似然度累积分布Fig.9 Cumulative belief and plausibility distribution for displacement constraint

由图7可知，该算法具有很高的计算效率，25杆桁架形状的优化计算在迭代大约100次后已经收敛.从图9和表3可以看出，在Pf＝0.1和Pf＝0.05两种情况下，位移约束失效概率[P（g2＜0）]的不确定区间[Bel，Pl]分别为[0，0.066]和[0，0.036]，失效似然度即概率上界均小于相应的失效概率许用值，满足设计可靠度的要求.由表3可知，由于考虑不确定性的存在，基于D－S可靠性优化结果总质量要比确定性优化结果有所增加，但是从失效似然度来看，前者的可靠性（93.4%，96.4%）要明显高于后者（5%）.由此可见，对不确定量的认识信息较少，无法采用概率理论时，证据理论以区间测度[Bel，Pl]代替传统概率单值来描述这种认知不确定显得更为合理.由于基于D－S的可靠性优化将使结构具有良好的鲁棒性，有效避免由于错误估计而造成优化结果的偏差.

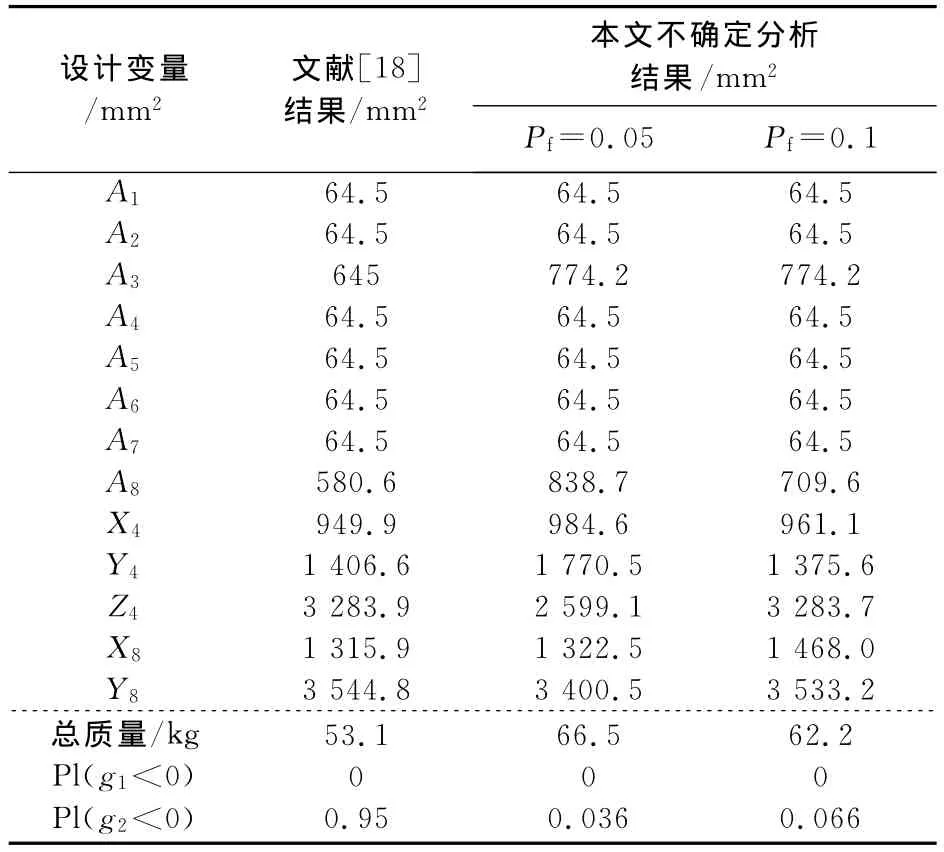
表3 25杆空间桁架形状优化结果比较Tab.3 Comparison of optimal designs for the 25－bar truss

4 结 论

可靠性优化设计中，由于不确定信息较少无法构造精确概率分布时，证据理论代替传统的概率理论进行不确定信息描述是一种理想的选择.该方法用不确定区间测度[Bel，Pl]代替不可知的真实概率来处理不完备的数据信息，以Pl（F）＜Pf作为概率可靠性约束条件的替代模型，本文同时引入微分演化算法提高求解联合焦元内反应区间极值的计算效率以及可靠性优化的寻优速度，降低证据理论在可靠性优化中的计算成本.

本文以25杆桁架形状优化为例，在考虑荷载和弹性模量均为不确定的情况下，基于D－S进行可靠性优化设计得到了很好的结果.分析结果表明，本文所提方法在实际工程中具有一定的应用前景.

[1] DEMPSTER A P.Upper and lower probabilities induced by a multiplicand mapping[J].Annals of Mathematical Statistics，1967，38：325－339.

[2] SHAFER G.A mathematical theory of evidence[M].Princeton：Princeton University Press，1976：9－50.

[3] MCCLEAN S，SCOTNEY B.Using evidence theory for the integration of distributed database[J].International Journal of Intelligent Systems，1997，12（10）：763－776.

[4] FRANCOIS J，GRANDVALET Y，DENOEUX T，etal.Adden－dum to resample and combine：an approach to improving uncertainty representation in evidential pattern classification[J].Information Fusion，2003（4）：75－85.

[5] 张晓明，王航宇，黄达.基于D－S证据理论的多平台协同数据融合[J].计算机工程，2007，33（11）：242－243.ZHANG Xiao－ming，WANG Hang－yu，HUANG Da.Cooperative multi－platform data fusion based on D－S evidence theory[J].Computer Engineering，2007，33（11）：242－243.（In Chinese）

[6] 郝军，吴炜，杨栈.改进D－S算法在船舶汽轮机故障诊断中的应用研究[J].船海工程，2007，36（3）：49－51.HAO Jun，WU Wei，YANG Zhan.Application of the improved D－S algorithm in fault diagnosis of ship’s turbine－machinery[J].Ship ＆Ocean Engineering，2007，36（3）：49－51.（In Chinese）

[7] MOURELATOS Z P，ZHOU J.A design optimization method using evidence theory[J].Journal of Mechanical Design，ASME，2006，128（7）：901－908.

[8] BAE H R，GRANDHI R V，CANFIELD R A.Reliability－based design optimization under imprecise uncertainty[C]／／46th Structures，Structural Dynamics and Materials Conference，AIAA／ASME／ASCE／AHS／ASC，2005：3301－3313.

[9] 郭慧昕，刘德顺，胡冠昱，等.证据理论和区间分析相结合的可靠性优化设计方法[J].机械工程学报，2008，44（12）：36－41.GUO Hui－xin，LIU De－shun，HU Guan－yu，etal.Method of reliability design optimization using evidence theory and interval analysis[J].Chinese Journal of Mechanical Engineering，2008，44（12）：36－41.（In Chinese）

[10] 郭慧昕，夏立龙，戴娟.基于证据理论的结构失效概率计算方法[J].应用基础与工程科学学报，2008，16（3）：457－464.GUO Hui－xi，XIA Li－long，DAI Juan.Method for calculating the failure probability of engineering structure using evidence theory[J].Journal of Basic Science and Engineering，2008，16（3）：457－464.（In Chinese）

[11] 任丕顺.基于证据理论的气门弹簧可靠性设计优化[J].装备制造技术，2012（5）：49－52.REN Pi－shun.The reliability optimal design of the valve spring based on evidence theory[J].Equipment Manufacturing Technology，2010（5）：49－51.（In Chinese）

[12] 段新生.证据理论与决策、人工智能[M].北京：中国人民大学出版社，1993：13－32.DUAN Xin－sheng.Evidence theory and decision ＆artificial intelligence[M].Beijing：China Renmin University Press，1993：13－32.（In Chinese）

[13] SENTZ K，FERSON S.Combination of evidence in dempster－shafer theory，SAND2002－0835report[R].Sandia：Sandia National Laboratories，2002.

[14] BALLING R.Optimal steel frame design by simulated annealing[J].Journal of Structural Engineering，1991，117（6）：1780－1795.

[15] GOLDBERG D，KUO C.Genetic algorithms in pipeline optimization[J].Journal of Computing in Civil Engineering，1987，1（2）：128－141.

[16] 唐和生，范德伟，王兆亮，等.桁架尺寸优化微分演化算法[J].湖南大学学报：自然科学版，2011，38（11）：13－18.TANG He－sheng，FAN De－wei，WANG Zhao－liang，etal.Differential evolution algorithm to size the optimization of truss structures[J].Journal of Hunan University：Natural Sciences，2011，38（11）：13－18.（In Chinese）

[17] STORN R，PRICE K.Differential evolution—a simple and efficient adaptive scheme for global optimization over continuous spaces[J].Journal of Global Optimization，1997，11（4）：341－359.

[18] GHOLIZADEH S，BARATI H.A comparative study of three metaheuristics for optimum design of trusses[J].International Journal of Optimization in Civil Engineering，2012，3：423－441.