长周期随机地震作用下超大跨斜拉桥的行波效应分析＊

陈清军，张 婷，陈志海，张振炫

（同济大学 土木工程防灾国家重点实验室，上海 200092）

长周期地震动特性很复杂，受到震源、震中距和场地条件等因素的影响.由于长周期地震动记录和资料的匮乏，目前有关长周期地震动及其对结构影响的研究还不成熟.近年来，自振周期较长的结构在长周期地震动作用下遭受破坏的事例时有发生，例如在1985年墨西哥8.1级地震中，离震中约390 km的墨西哥城内高层建筑的破坏程度远重于低层楼房[1].在1989年美国 Loma Prieta地震中，距震中近100km的旧金山西北地区高架桥发生了较严重的破坏[2].在2003年日本十胜冲地震中，远离震中的苫小牧地区储油罐发生严重溢流，并引发一场大火灾[3].这些震害表明，对于自振周期较长的结构抗震问题需要进一步研究.

大跨度桥梁结构具有较长的自振周期，其抗震性能备受国内外学者的关注.文献[4]基于各模态振动特性的简化多支承激励反应谱法，分析了地震动空间变化对芜湖长江大桥主航道斜拉桥地震响应的影响.文献[5]利用Abaqus软件建立三塔悬索桥分析模型，进行了行波作用下的桥梁结构非线性地震响应分析.Allam等[6]采用反应谱方法对一斜拉桥结构进行了多点激励下的地震反应研究.Wang等[7]考虑桥墩高度、激励方向和视波速的不同，对4座连续梁桥进行了多种工况下的弹塑性行波效应研究.至今有关大跨桥梁结构的地震反应研究大多是基于普通地震动作用下的确定性地震反应问题.

本文从各个国家和地区的地震记录库中寻找出一些具有良好记录质量和基本场地资料的强震记录，参照文献[8]对长周期地震动的概念描述，把收集到的1 081条地震波分为长周期地震波和普通地震波两大类，对比分析不同场地条件下长周期地震波和普通地震波的平均加速度反应谱及其规范形式的分段拟合谱；选取软土场地拟合反应谱作为目标反应谱，用迭代方法求取与目标反应谱相对应的功率谱密度函数，分析基于长周期地震动加速度功率谱密度的特点，并以某超大跨斜拉桥结构为背景，采用直接求取位移的改进虚拟激励法，研究长周期随机地震作用下超大跨斜拉桥的行波效应.

1 结构多点随机地震反应分析基本方程

多点激励下的结构运动方程可表达为[9]：

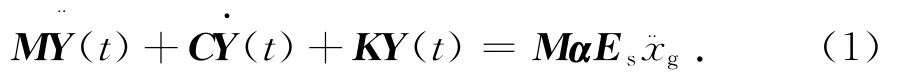
式中：M，C和K分别为结构质量、阻尼和刚度矩阵；Y（t）为体系的动力相对位移向量；α为拟静模态矩阵；Es为结构非支座节点惯性力指示向量；为结构支座在地震波传播方向上的地面加速度.

为研究多点随机地震激励下的结构地震反应问题，可以在频域内将空间地震动模型表达为[10]：

式中：Sjj（ω）为自功率谱；Cjk（ω）和Qjk（ω）分别为互功率谱的实部和虚部.每个激励点可按下述关系式输入：

式中：S0（ω）为激励点输入功率谱；djk为激励点j，k两点连线沿地震波传播方向的投影距离；Va为地震波视波速.

对大型结构进行随机地震反应分析，虚拟激励法较传统的随机振动理论求解方法，计算效率可提高2～4个数量级[10－11].本文选用高精度的直接位移求解的虚拟激励法[11]，利用对ANSYS程序的二次开发，实现了对长周期随机地震作用下超大跨斜拉桥结构的行波效应计算与分析.这一方法可避免常规虚拟激励法需分别计算拟静力和动态相对位移的过程，更为高效；完成本文一个完整工况的计算，耗时约45min（Intel I5－2310计算机）.

2 输入功率谱密度函数的确定

2.1 目标反应谱的求取

自从反应谱理论提出以来，已有很多学者对反应谱的特性作过各种研究.但是，在数字强震仪问世以前，由于受强震仪频率特性的限制，很难从强震记录中获得真实可靠的长周期频谱信息[8].因此，以往的反应谱特性研究大多只限于周期6s以下的范围.进入20世纪80年代以来，数字强震仪获得了迅速发展并已在一些国家和地区投入使用.数字强震仪的频率通常在0～30或50Hz左右，可以较好地记录到地震动的高、低频信息.而且，由于不需要进行人工数字化处理，避免了由此带来的长周期数字化误差.所以，数字强震仪记录是研究地震动长周期特性的可靠资料[8].

本文从国内外数字强震记录库（美国太平洋地震工程研究中心、日本地球科学和防灾国家研究所、中国国家强震动台网中心）中，选取有较好记录质量和具有基本场地资料的1 081条地震加速度水平分量记录，包括1985年墨西哥8.1级地震、1999年中国台湾集集7.6级地震、2003年日本十胜冲8.0级地震、2008年汶川8.0级地震和2011年3.11日本9.0级大地震.选取情况如表1所示.

参照文献[8]对长周期地震动的表述，将所选地震波分为长周期和普通地震波两大类.这里所谓的长周期是指具有工程意义上的长周期（其范围通常为1或2秒至十几秒），而不是地震学上周期长达几分或十几分钟的长周期振动.所有加速度记录都采用统一低频误差校正，峰值大于10gal，利用强震地震动时程直接计算反应谱方法解决反应谱的长周期段取值问题，反应谱均计算到周期10s.

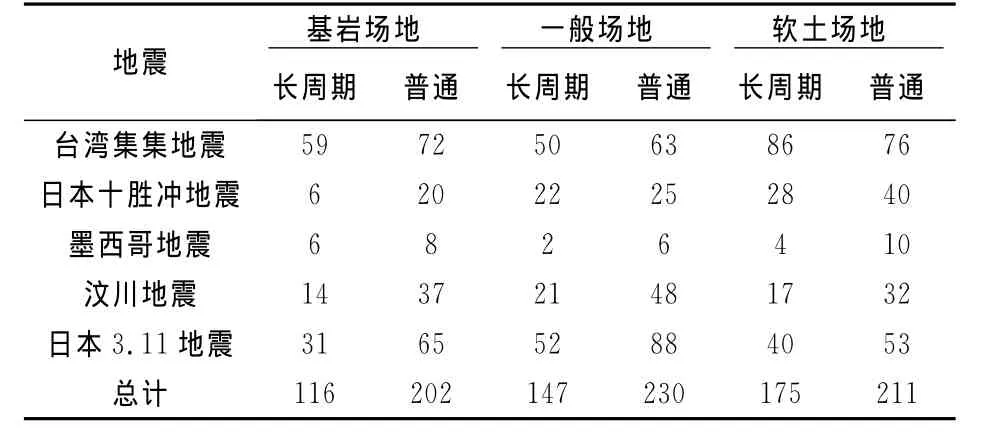
表1 强震记录选取情况表Tab.1 Selected strong motion records

首先，计算出集集、日本十胜冲、汶川和日本3.11等4次地震记录的平均放大系数反应谱后，再与墨西哥地震记录相应的反应谱作平均，并对其进行最小二乘法拟合.具体表达式如下：

式中：为统计的平均放大系数反应谱值；βi为拟合后的谱值.建议长周期衰减部分采用不分段形式进行拟合，且函数形式如下：

对于一定的T1和r，求βmax和Tg，使R取最小值且满足下列方程：

其次，在拟合放大系数反应谱的基础上，根据规范按抗震设防烈度7度多遇地震下水平地震影响系数最大值，计算出绝对加速度反应谱.图1和图2分别给出了三类场地条件下长周期地震动和普通地震动的平均加速度反应谱和拟合反应谱比较曲线（阻尼比ξ＝0.05），表2给出了相应的反应谱特征参数取值.由图1可见，普通地震动的平均加速度反应谱的衰减速度明显大于长周期地震动，对于基岩场地和一般场地，至10 s时基本接近0，而长周期地震动的平均加速度反应谱仍有一定谱值；对于软土场地，至10s时长周期地震动的平均加速度反应谱值约为普通地震动谱值的2倍.由图2可见，长周期地震动拟合反应谱的平台宽度明显大于普通地震动的拟合反应谱平台宽度；对于本文拟选用的软土场地拟合反应谱，对应的长周期地震动拟合反应谱平台值为0.770m·s－2，特征周期Tg＝1.348s，而普通地震动拟合反应谱平台值为0.834m·s－2，特征周期Tg＝0.965s.

图1 不同场地条件下的平均加速度反应谱（阻尼比为0.05）Fig.1 Average acceleration response spectra at different sites（damping ratio 0.05）

图2 不同场地条件下的拟合加速度反应谱（阻尼比为0.05）Fig.2 Fitted acceleration response spectra at different sites（damping ratio 0.05）

表2 三类场地标准加速度反应谱特征参数取值表Tab.2 Characteristic parameters of normalized acceleration response spectra at three types of sites

2.2 将目标反应谱转换成当量功率谱密度

可采用迭代法，将目标反应谱转换成平稳随机地震动功率谱密度函数.其主要步骤如下[12]：

1）选择功率谱密度函数的初值G0（ωi）（i＝0，1，…，N），最简单的可设G0（ωi）为一常值，即为一平稳白噪声过程，为减少迭代次数，本文采用Kaul[13]的公式进行计算.

2）对在平稳地面运动加速度功率谱G（ω）作用下，求取具有圆频率为ωi、阻尼比为ξ的振子的绝对加速度反应最大值均值Am：

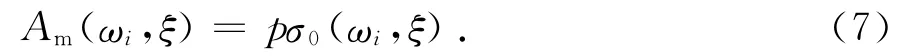
其中：

式（8）中ντ统一按 Der Kiureghian[14]的经验公式进行计算.

3）把G0（ωi）代入式（7）中计算Am（ωi，ξ），将其与目标反应谱Ra（ωi，ξ）比较.直至所有点误差满足要求，方可停止迭代.在结构随机地震反应分析中，日本学者Kanai－Tajimi的过滤白噪声模型得到了较多的应用.这一模型假设在基岩输入白噪声过程，将基岩上的覆盖土层视为单自由度线性滤波器，经过滤后求得地表面的功率谱密度函数表达式.已有研究表明，Kanai－Tajimi的过滤白噪声模型夸大了低频地震动的能量.基于此，文献[15]提出了一种削减低频的改进模型，即

式中：ωg，ξg分别为场地土卓越频率和阻尼比；ωf和ξf分别为调整低频部分的频率和阻尼参数；S0为白噪声功率谱密度.研究表明Clough－Penzien模型能较好地反映地震动低频能量的变化[15]，因此，本文选用这一模型拟合功率谱密度函数，并以此作为超大跨斜拉桥结构随机地震反应分析用的输入.

采用上述迭代方法求出与图2软土场地目标反应谱对应的功率谱密度函数，然后选用最小二乘法拟合出与目标反应谱相对应的Clough－Penzien谱参数（见表3）.图3给出了基于图2（c）软土场地目标反应谱（Ⅲ类场地、7度多遇地震、设计地震分组第2组）拟合后的当量平稳功率谱密度函数曲线.由此可见，基于长周期地震动记录的功率谱密度函数的频谱分布与基于普通地震动记录的功率谱密度函数的频谱分布有明显差异，前者的卓越频率明显低于后者.

图3 拟合功率谱密度函数曲线对比Fig.3 Comparison between fitted earthquake acceleration power spectra with long periods and with general periods

表3 与目标反应谱对应的Clough－Penzien功率谱参数Tab.3 Clough－Penzien power spectrum parameters corresponding to the target response spectra

3 超大跨桥梁结构有限元模型及动力特性分析

本文以某超大跨桥梁结构为背景建立有限元分析模型.该桥为双塔双索面斜拉桥，采用漂浮结构体系；全长32.4km，主要由跨江大桥和南、北岸接线3部分组成.工程抗震设防烈度为7°，抗震等级为一级，场地类别为Ⅲ类.主桥跨径为100m＋100m＋300m ＋1 088m ＋300m ＋100m ＋100m，其中钢箱梁分为141个梁端，17种类型；边跨尾索区节段长为12m，其他节段均为16m.塔柱高达300.4m，采用倒Y形结构，分为上、中、下塔肢和横梁4个部分；中、下塔肢为钢筋混凝土结构，上塔肢为钢锚箱－混凝土组合结构.两主墩分别采用131根长约120m的灌注群桩基础.全桥共有34×8＝272根斜拉索，选用φ7平行钢丝体系.

采用ANSYS软件建立该超大跨斜拉桥结构有限元计算模型，如图4所示.主梁、索塔、塔横梁、辅助墩及过渡墩均采用BEAM44单元，鱼刺刚臂采用BEAM4单元，斜拉索采用LINK10单元，桥面二期恒载及箱梁内压重块附加质量采用质量MASS21单元进行模拟，考虑到斜拉索索段垂度的影响，斜拉索弹性模量用Ernst公式修正.索塔与主梁间纵桥向、竖向均自由，横桥向主从约束；过渡墩、辅助墩与主梁之间竖向、横桥向均约束，纵桥向自由.

图4 某超大跨斜拉桥结构有限元模型Fig.4 Finite element model of a long－span cable－stayed bridge

利用图4的某超大跨斜拉桥结构有限元模型，采用子空间迭代法进行结构动力特性分析，获得了这一超大跨斜拉桥结构的前20阶自振频率和振型.限于篇幅，仅给出部分结构自振频率和相对应的振型说明，如表4所示.由表4可见，这一超大跨斜拉桥结构的基本周期长达12.67s，属于典型的长周期类结构；其自振频率变化均匀且较密集，无跳越现象.结构振型则表现出明显的三维性和相互耦合的特点：第1阶振型为主梁纵向漂移，符合漂浮体系特点，纵飘对桥梁结构纵向地震反应的贡献较大；第2阶振型为主梁对称横弯，该振型对桥梁结构侧向位移有一定的影响；第3阶振型为主梁对称竖弯，将对桥梁结构的竖向地震反应有较大的影响.

表4 大桥自振频率及振型特点Tab.4 Natural frequencies and vibration modes of the bridge

4 结构随机地震反应分析

将图3所示的基于不同类型地震动记录的功率谱密度作为输入，利用图4所示的某超大跨斜拉桥结构有限元模型，采用直接求取位移的改进虚拟激励法，假定地震波沿桥梁纵向（X方向）自左塔向右塔传播，对超大跨桥梁结构进行了非一致激励下的随机地震反应分析.限于篇幅，这里重点对基于不同类型地震动记录的功率谱密度作用下桥梁左桥塔顶601号节点、右桥塔顶1 601号节点和桥面板跨中71号节点的随机地震反应进行比较分析.

图5和图6分别给出了基于不同类型地震动记录的功率谱密度作用下桥梁左桥塔顶和右桥塔顶的水平向位移响应功率谱曲线.图7给出了桥面板跨中71号节点的竖向位移响应功率谱曲线.由图5～图7可见，长周期地震动功率谱作用下的桥梁左桥塔顶、右桥塔顶和桥面板跨中节点的位移响应功率谱值均明显大于普通地震动功率谱作用下的结果；桥梁塔顶位移响应功率谱均呈双峰分布，但最大峰值出现的位置不同，在长周期地震动功率谱作用下的最大峰值出现在较低频率（即结构基频0.079 Hz）处，而在普通地震动功率谱作用下的最大峰值则出现在较高频率（即结构第3阶自振频率处0.183Hz）处.

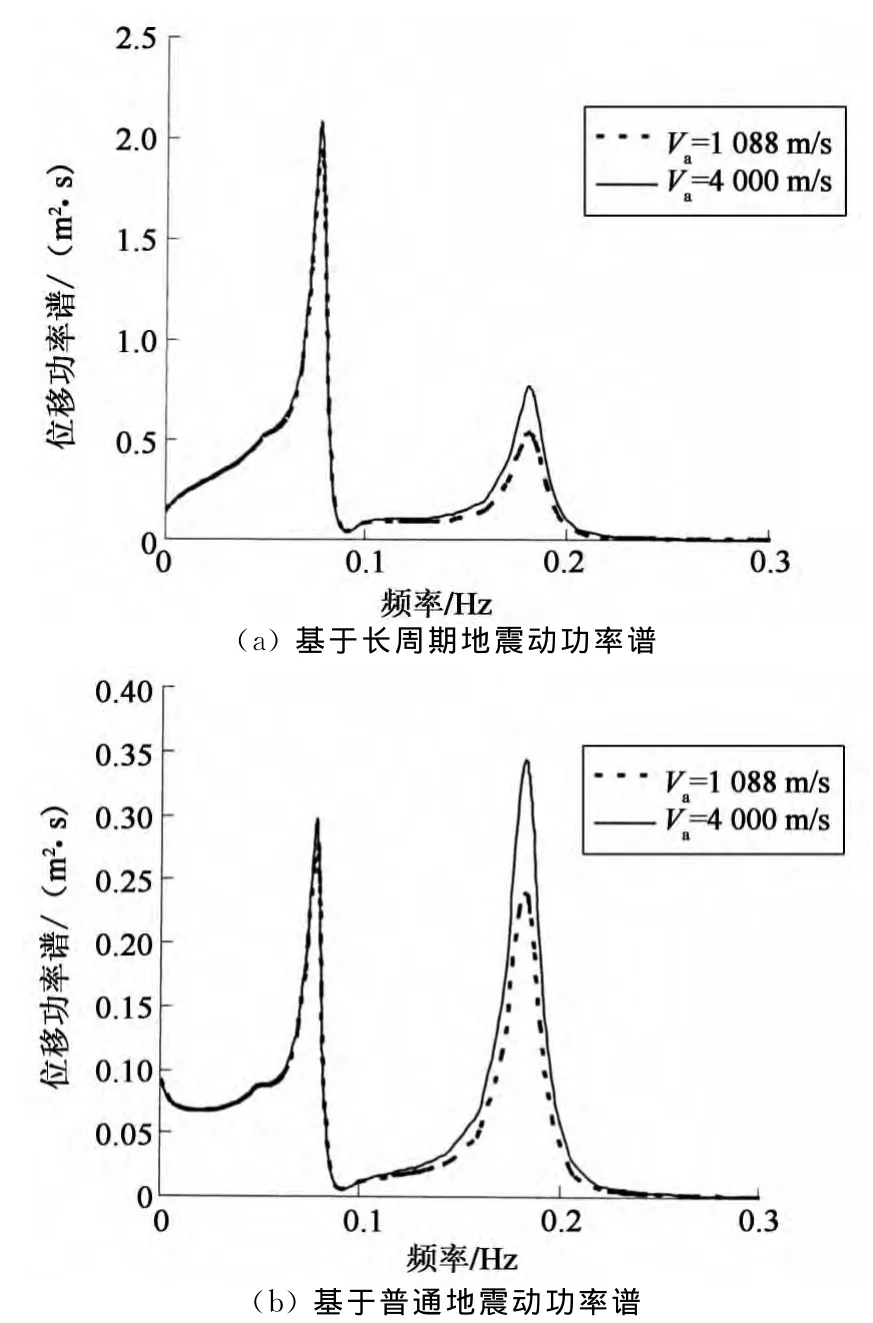
图5 左塔塔顶水平向位移响应功率谱曲线Fig.5 Horizontal displacement response power spectra curves of the left tower top

图6 右塔塔顶水平向位移响应功率谱曲线Fig.6 Horizontal displacement response power spectra curves of the right tower top

图7 桥面板跨中竖向位移响应功率谱曲线Fig.7 Vertical displacement response power spectra curves of the mid－deck

为考察不同地震动功率谱作用下超大跨斜拉桥位移响应和弯矩响应的最大值均值随桥塔塔高和桥面板位置的变化情况.图8（a）给出了基于不同类型地震动记录的功率谱作用下桥梁左塔位移响应最大值均值随塔高的分布图；利用结构随机振动基本公式求取弯矩的最大值均值[16]，图8（b）给出了桥梁左塔弯矩最大值均值随塔高的分布.图9（a）和（b）分别给出了不同输入功率谱作用下桥面板位移响应和弯矩响应最大值均值沿桥面纵向的分布.

图8 桥梁左塔位移及弯矩最大值均值沿塔高分布图Fig.8 The mean curves of maximum displacement and bending values of the left tower in the vertical direction

图9 桥面板位移及弯矩最大值均值沿桥面纵向分布图Fig.9 The mean curves of maximum displacement and bending values of the deck in the longitudinal direction

在长周期地震动功率谱作用下桥梁左塔位移响应和弯矩响应最大值均值随塔高的变化趋势、以及桥面板位移响应和弯矩响应最大值均值沿桥面纵向的变化趋势，均与普通地震动功率谱作用下的变化趋势相近；但长周期地震动功率谱作用下结构位移响应和弯矩响应最大值均值均明显大于普通地震动功率谱作用下的结果.

为进一步分析长周期随机地震作用下超大跨斜拉桥的行波效应，本文对4种视波速分别为Va＝1 088m／s，Va＝2 500m／s，Va＝4 000m／s，Va＝∞（一致激励）情形下斜拉桥结构的长周期随机地震响应结果进行了对比研究.图10（a）和（b）分别给出了4种视波速情形下桥梁左塔位移响应和弯矩响应最大值均值随塔高的分布图.图11（a）和（b）分别给出了4种视波速情形下桥面板位移响应和弯矩响应最大值均值沿桥面纵向的分布.

在视波速Va＝1 088m／s情形下，桥梁左塔塔顶的位移响应最大值均值和塔底弯矩的最大值均值较一致激励（Va＝∞）下的结果减小约10%；在视波速Va＝4 000m／s情形下，桥梁左塔塔顶的位移响应最大值均值和塔底弯矩的最大值均值与一致激励下的结果接近.行波效应对桥面板主跨跨中位移影响较大，而对桥面板边跨位置的影响较小；当视波速介于1 088m／s和2 500m／s之间时，主跨桥面板跨中位移的最大值均值较一致激励下的结果减小约15%.

图10 长周期地震动功率谱作用下左塔位移及弯矩最大值均值沿塔高分布图Fig.10 The mean curves of maximum displacement and bending values of the left tower in the vertical direction for the input long－period ground motion power spectrum

图11 长周期地震动功率谱作用下桥面板位移及弯矩最大值均值沿桥面纵向分布图Fig.11 The mean curves of maximum displacement and bending values of the deck in the longitudinal direction for the input long－period ground motion power spectrum

5 结 论

1）本文从各个国家和地区的地震记录库中寻找出1 081条具有良好记录质量和基本场地资料的地震波，对比分析了不同场地条件下长周期地震波和普通地震波的平均加速度反应谱曲线.结果表明，普通地震波的平均加速度反应谱的衰减速度明显大于长周期地震波反应谱.对于软土场地，长周期地震波的平均加速度反应谱值至10s时约为普通地震波谱值的2倍.

2）长周期地震动拟合反应谱的平台宽度明显大于普通地震动的拟合反应谱平台宽度；基于长周期地震动记录的功率谱密度函数的频谱分布与基于普通地震动记录的功率谱密度函数的频谱分布有明显差异，前者的卓越频率明显低于后者.

3）长周期地震动功率谱作用下的桥梁左桥塔顶、右桥塔顶和桥面板跨中节点的位移响应功率谱值均明显大于普通地震动功率谱作用下的结果；桥梁塔顶位移响应功率谱均呈双峰分布，但最大峰值出现的位置不同，在长周期地震动功率谱作用下的最大峰值出现在较低频率处，而在普通地震动功率谱作用下的最大峰值则出现在较高频率处.

4）对于本文算例，在视波速Va＝1 088m／s情形下，桥梁左塔塔顶的位移响应最大值均值和塔底弯矩的最大值均值较一致激励下的结果减小约10%；而在视波速Va＝4 000m／s情形下，桥梁左塔塔顶的位移响应最大值均值和塔底弯矩的最大值均值与一致激励下的结果接近.行波效应对桥面板主跨跨中位移影响较大，而对桥面板边跨位置的影响较小；当视波速为1 088～2 500m／s时，主跨桥面板跨中位移的最大值均值较一致激励下的结果减小约15%.

[1] KOKETSU K，MIYAKE H.A seismological overview of long－period ground motion[J].Journal of Seismology，2008，12（2）：133－143.

[2] 汪素云，俞言祥，吕红山.利用中国数字地震台网宽频带记录研究长周期地震动反应谱特性[J].地震学报，1998，20（5）：481－488.WANG Su－yun，YU Yan－xiang，LV Hong－shan.Study on response spectrum characteristics of long－period earthquake ground motion using wide band records from Chinese Digital Seismic Network [J].Seismological Journal，1998，20（5）：481－488.（In Chinese）

[3] 李春锋，张旸.长周期地震动衰减关系研究的迫切性[J].地震地磁观测与研究，2006，27（3）：1－8.LI Chun－feng，ZHANG Yang.Urgency of the study of longperiod ground motion [J].Seismological and Geomagnetic Observation and Research，2006，27（3）：1－8.（In Chinese）

[4] 刘洪兵，朱晞.大跨度斜拉桥多支撑激励地震响应分析 [J].土木工程学报，2001，34（6）：38－44.LIU Hong－bing，ZHU Xi.Seismic response analysis of longspan cable－stayed bridges under multi－sport excitations[J].China Civil Engineering Journal，2001，34（6）：38－44.（In Chinese）

[5] 焦常科，李爱群，操礼林，等.三塔悬索桥行波效应研究[J].土木工程学报，2010，43（12）：100－106.JIAO Chang－ke，LI Ai－qun，CAO Li－lin，etal.Traveling wave influence analysis for triple－tower suspension bridges[J].China Civil Engineering Journal，2010，43（12）：100－106.（In Chinese）

[6] ALLAM S M，DATTA T K.Analysis of cable－stayedbridges under multi－component random ground motion by response spectrum method[J].Engineering Structures，2000，22（10）：1367－1377.

[7] WANG J，CARR A J，COOKE N，etal.The response of a 344mlong bridge to non－uniform earthquake ground motions[J].Engineering Structures，2009，31（11）：2554－2567.

[8] 谢礼立，周雍年，胡成祥，等.地震动反应谱的长周期特性[J].地震工程与工程振动，1990，10（1）：1－19.XIE Li－li，ZHOU Yong－nian，HU Cheng－xiang，etal.Characteristics of response spectra of long－period earthquake ground motion[J].Earthquake Engineering and Engineering Vibration，1990，10（1）：1－19.（In Chinese）

[9] CLOUGH R W，PENZIEN J.Dynamics of structures[M].New York：McGraw－Hill，1993：146－149.

[10] 林家浩，张亚辉.随机振动的虚拟激励法[M].北京：科学出版社，2004：129－134.LIN Jia－hao，ZHANG Ya－hui.The pseudo－excitation method of random vibration[M].Beijing：Science Press，2004：129－134.（In Chinese）

[11] 李永华，李思明.绝对位移直接求解的虚拟激励法[J].振动与冲击，2009，28（10）：185－190.LI Yong－hua，LI Si－ming.Pseudo excitation method based on solving absolute displacement[J].Journal of Vibration and Shock，2009，28（10）：185－190.（In Chinese）

[12] 孙景江，江近仁.与规范反应谱相对应的金井清谱的谱参数[J].世界地震工程，1990，8（1）：42－48.SUN Jing－jiang，JIANG Jin－ren.Spectrum parameters corresponding to the response spectra of seismic design code[J].World Earthquake Engineering，1990，8（1）：42－48.（In Chinese）

[13] KAUL M K.Stochastic characterization of earthquakes through their response spectrum[J].Earthquake Engineering and Structural Dynamics，1978，6（5）：497－509.

[14] DER KIUREGHIAN A.Structural response to stationary excitation[J].Journal of the Engineering Mechanics Division，1980，EM6：203－235.

[15] DUMANOGLUID A A，SOYLUK K.A stochastic analysis of long span structures subjected to spatially varying ground motions including the site－response effect [J].Engineering Structures，2003，25（10）：1301－1310.

[16] 欧进萍，王光远.结构随机振动[M].北京：高等教育出版社，1998：371－373.OU Jin－ping，WANG Guang－yuan.Random vibration of structures[M].Beijing：Higher Education Press，1998：371－373.（In Chinese）