基于分形理论超轻中空二次粒子纤维壁的有效导热系数计算方法

，，

(1. 海军工程大学 舰船高温结构复合材料研究室，武汉 430033;2. 海军工程大学 动力工程学院，武汉 430033)

0 引 言

硬硅钙石晶体纤维缠绕形成的超轻中空二次粒子是一种新型的多孔绝热材料，具有超轻的密度、优良的绝热保温性能、人体友好性和高利用率的特点，近年来得到高度重视，发展非常迅速[1]。硬硅钙石型硅酸钙绝热材料按制品密度可分为220 kg/m3左右的普通型和小于135 kg/m3的超轻型两类，其中孔隙率分别为0.919和大于0.95，属于高孔隙率的多孔绝热材料。

多孔绝热材料的导热系数是衡量其绝热性能的重要参数。建立起计算其导热系数的模型，并分析各个因素对其导热性能的影响，对于提高材料的绝热性能具有十分重要的意义[2]。在研究过程中，多孔材料内部几何结构的不规律性导致其物性参数的不确定性，在理论研究时，很难用传统方法对其导热性能进行准确的描述。以往的研究大都基于连续介质假设和容积平均的方法，仅用孔隙率这一个参数描述多孔材料的空间结构，但事实上，孔隙率相同的多孔材料，内部固相尺度和分布不同，其导热系数也不同。

20世纪80年代以来，分形理论开始被引入多孔介质的传热研究中来[3]。Yongjin Feng、Boming Yu等[4]基于分形理论，利用Sierpinski地毯模拟连续孔隙的两相多孔介质，推导了其有效热导率数学模型。王唯威等[5]基于分形理论，构造了不同分形模型来模拟分形介质，采用有限容积法对导热问题进行了数值模拟与分析。以上分形模型不含经验常数，参数较少，计算简便，但不同种多孔介质材料内部结构的分形特征不同，因此针对某种特定的材料，推导反映其内部微尺度结构特征的传热模型具有重要意义。施明恒[6]等利用分形方法对聚氨酯泡沫塑料微观泡孔结构和导热特性进行了研究，提出了计算聚氨酯泡沫塑料导热的简化分形模型。徐平[7]采用分形理论对泡沫铝材料的微观结构进行了研究，利用面积-周长分维算法证明了其微观结构在一定尺度内具有自相似特点。本文的主要工作是针对所研究的硬硅钙石超轻中空二次粒子，证明其纤维分布具有分形特征，并建立反映其纤维微观分布特点的分形导热模型。

1 硬硅钙石超轻中空二次粒子纤维壁的微尺度空间结构及分形描述

1.1 微尺度空间结构

硬硅钙石型硅酸钙绝热材料是一种高孔隙率的绝热材料，是由针状硬硅钙石晶体纤维缠绕组成的球状团聚体，外壳密实，内部中空，这种球形聚合体被成为硬硅钙石二次粒子。

如图1所示为硬硅钙石二次粒子表面纤维及孔隙微观结构的电子显微镜扫描图，可以看出晶体纤维相互交错，形成的几何结构复杂多变，且纤维呈随机排列，因此，很难用数学方法对其真实导热情况加以准确描述。利用分形的相似性对其复杂结构进行简化，建立简化的分形导热模型，根据等效热阻方法，可以推导出其有效导热系数的分形计算式。

图1 硬硅钙石二次粒子及纤维壁缠绕的纤维形貌

1.2 分形描述

分形几何学是一门以非规则几何形状为研究对象的几何学，如土壤、海岸线、多孔材料等，其内部发生的过程不能用简单的线性近似方法来认识和描述。分形理论为描述自然界中非线性现象和几何形状、物体内部的复杂结构和空间分布提供了一种行之有效的手段，从而为精确研究复杂结构内部客观规律开辟了一条新路[8]。根据分形理论，存在于df维欧氏空间中的一个多孔分形体的面积、体积或长度等物理量N(r)与物体度量尺度r有以下自相似标度关系：

N(r) ∝rdf。

(1)

式中：N为分形物体的空间占有积(线、面或体)；r为度量尺度；df为分形维数，可以是整数也可以是非整数，两物体只要满足分形维数相等，那么这两个物体是自相似的。根据分形理论，硬硅钙石超轻中空二次粒子纤维壁的纤维分布若满足分形特征，须满足以下关系式：

N(r)=Crdf。

(2)

式中：C为比例常数。等号两边取对数得：

logN(r)=logC+dflogr。

(3)

查找硬硅钙石纤维的场发射扫描电镜照片可以发现，二次粒子纤维直径最大特征尺寸B=100 nm，最小特征尺寸A=35 nm，对于在B→A的不同长度度量尺度r，对硬硅钙石二次粒子壳体表面纤维电镜扫描照片进行计盒维数计算。采用差分计盒维数算法，此算法在计算灰度图像时，简单、快速、精确。经计算可以看出硬硅钙石二次粒子纤维壁的纤维分布满足分形特征，对于被测样品(表观密度ρ=125 kg·m-3)其分形维数为df=2.516 8。

实际硬硅钙石二次粒子纤维及孔隙的几何结构是复杂多变的，纤维排列既可能是有序的，又可能是无序排列。利用分形的相似性对其复杂的几何结构进行简化，假定硬硅钙石二次粒子纤维壁的纤维排列呈多边形结构，建立分形等效模型如图3所示，图3为硬硅钙石二次粒子纤维壁截面简化模型，进而可把每一个多边形简化为具有相同截面积的正方形网格，即分形单元体。

图2 硬硅钙石二次粒子纤维壁电镜扫描照片分形维数计算

图3 二次粒子纤维壁截面简化模型与分形单元体模型

2 分形模型的有效导热系数

硬硅钙石二次粒子纤维壁有效导热系数Ke除与组成材料的各相自身导热系数有关外，还与其空间结构(孔隙率、分形维数)有关，这里用孔隙率和分形维数作为描述材料的空间结构的主要参数。根据分形理论，有效导热系数可以表示为：

Ke=f(∑Ki,Φ,df,T)。

(4)

式中：Ki为硬硅钙石二次粒子纤维壁的气相、固相的导热系数；φ为硬硅钙石二次粒子纤维壁纤维的体孔隙率；df为硬硅钙石二次粒子纤维壁孔隙分形维数；T为材料的温度。

根据孔隙率定义，孔隙率为孔隙体积和总体积的比值，结合文献[9]、[10]给出的计算分形体孔隙率的方法，孔隙率φ为：

(5)

式中：φ为材料的体孔隙率；L为度量尺度。

在纤维长度方向、热流方向、热流垂直方向上同时取长度为L的尺度，构成立方体导热单元体，于是硬硅钙石二次粒子纤维壁的热传递模型可简化为如图4所示。假设为一维稳态传热，热流方向自上而下，单元体上下边界温度分别为T1和T2，其他边界取绝热条件。

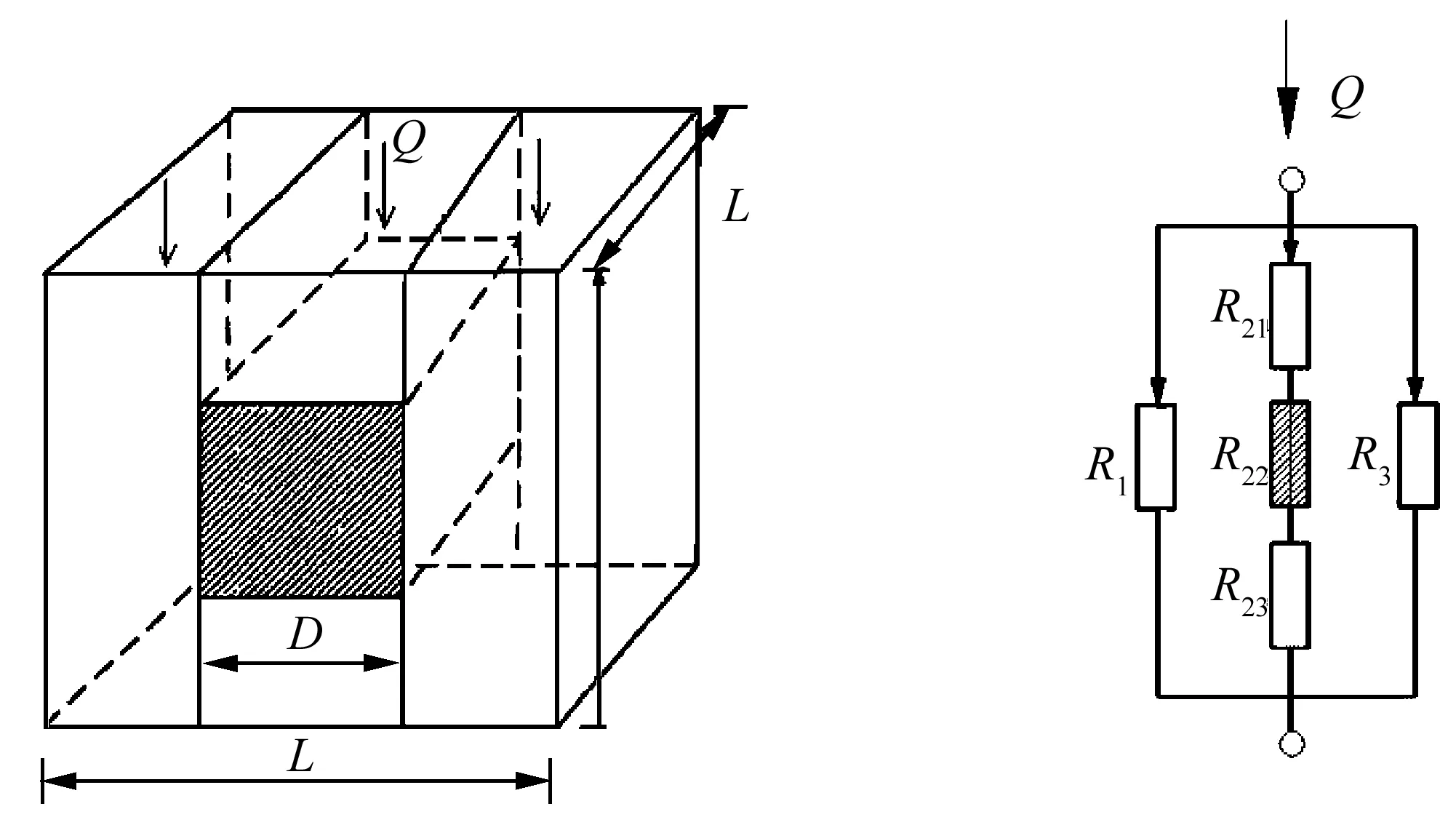
图4 单元体导热模型和等效热阻网络

从图4可以看出，左侧通道的气体热阻R1为：

R1=L/(KgA1)=2/[Kg(L-D)]。

(6)

中间通道的总热阻R2为：

R2=R21+R22+R23= (L-D)/(KgA2)+

D/(KsA2)=(L-D)/(KgDL)+1/(KsL)。

(7)

右侧通道的热阻R3为：

R3=R1=2/[Kg(L-D)]。

(8)

单元体的总热阻为：

R总=(R1R2R3)/(R2R3+R1R3+

R1R2)= [L(L-D)Ks+LDKg]/{LDKsKg+

Kg(L-D)[Ks(L-D)+KgD]}。

(9)

式中：D为单元体内纤维截面的等效正方形的边长；A1，A2分别左侧通道和中间通道在热流方向上的传热面积；Kg为气相导热系数；Ks为固相导热系数。

由傅立叶定律，总热流Q为：

Q=(T1-T2)/总=KcA(T1-T2)/L。

(10)

式中：A为单元体总传热面积。

分形单元体模型的有效导热系数为：

Ke=L/(AR总)=1/(LR总) =(1-D/L)Kg+

1/[(L/D-1)( 1/Kg) +1/Ks)]。

(11)

将(5)式带入(11)，可得：

Ke=[1-(1-φ)1/df]Kg+1/ {(1/Kg)

[ (1-φ)-1/df-1] +1/Ks)}。

(12)

从(12)式可以看出，硬硅钙石二次粒子纤维壁的有效导热系数与各相自身的导热系数有关，也与材料的微观结构(分形维数、孔隙率)有关。因此在对材料的热物性进行优化设计时，不仅要考虑材料自身的热物性参数，还要考虑材料的孔隙率与微观结构。

3 影响硬硅钙石二次粒子纤维壁有效导热系数的因素分析

3.1 参数的确定

固相导热系数Ks为硬硅钙石针状晶体的导热系数，采用来估计。这里f1、f2、f3分别是二氧化硅、氧化钙和水的摩尔百分数。魏高升[11]对文献[11]中的数据进行多项式拟合，得到了二氧化硅、氧化钙和水的导热系数关于温度的表达式：

KSiO2=0.752 33+0.003 13T-4 052 647×

10-6T2+3.526 37×10-9T3。

(13)

KCaO=1.290 23-9.241 18×10-5T-

1.271 45×10-7T2。

(14)

KH2O=-1.088 92+0.011 13T-2.266 28×

10-5T2+1.477 69×10-8T3。

(15)

式中:Kg为环境压力下空气随温度变化的导热系数，单位为W·m-1·K-1，计算公式为：

Kg=3.954×10-3+7.720 8×10-5T-

1.608 2×10-8T2。

(16)

将各参数的表达式带入式(12)即可计算出硬硅钙石二次粒子纤维壁有效导热系数Ke。

3.2 温度与硬硅钙石二次粒子纤维壁有效导热系数的关系

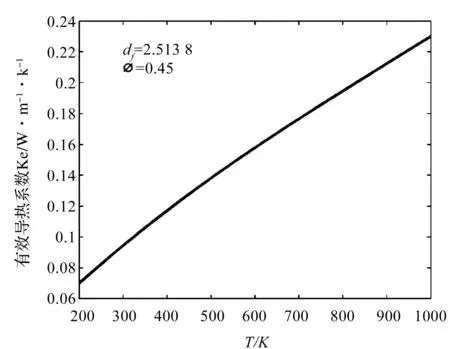
图5 硬硅钙石二次粒子纤维壁有效导热系数随温度变化的关系

取硬硅钙石二次粒子纤维壁的孔隙率为0.45[12]，取温度变化范围为200～1 000 K,得到材料有效导热系数随温度变化曲线如图5所示，可以看出随温度的升高，有效导热系数增大。

3.3 孔隙率与硬硅钙石二次粒子纤维壁有效导热系数的关系

孔隙率与硬硅钙石二次粒子纤维壁有效导热系数的关系，如图6所示。

图6 硬硅钙石二次粒子纤维壁有效导热系数随孔隙率变化的关系

计算得到材料的分形维数为df=2.51 68，当温度为T=300 K时，可得到硬硅钙石二次粒子纤维壁有效导热系数随孔隙率变化曲线如图6所示。由图6所示，材料的有效导热系数随孔隙率的增大而减小，这是因为气相的导热系数远小于固相的导热系数。当材料的孔隙率较小时，其有效导热系数随之增加而减小的幅度大；当材料的孔隙率较大时，其有效导热系数随之增加而减小的幅度小。

3.4 分形维数与硬硅钙石二次粒子纤维壁有效导热系数的关系

分形维数与硬硅钙石二次粒子纤维壁有效导热系数的关系，如图7所示。

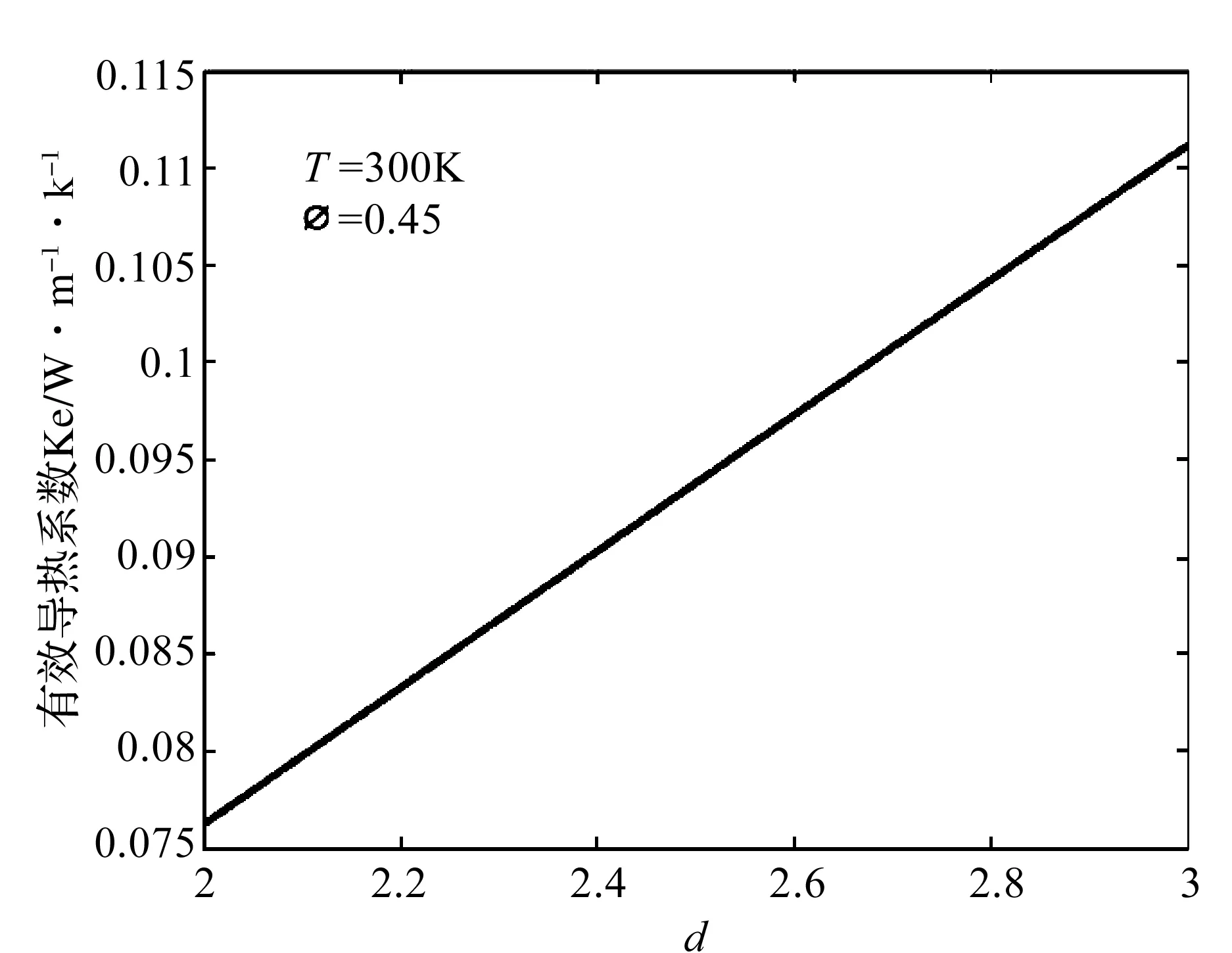
图7 硬硅钙石二次粒子纤维壁有效导热系数随分形维数变化的关系

图7给出了T=300 K，φ=0.45时，材料有效导热系数随分形维数的变化曲线。由图7可以得出即使是孔隙率相同的同种材料，当内部固相的尺度或者分布(分形维数描述)不同时，其有效导热系数也不同。

4 结束语

(1)采用分形理论分析硬硅钙石二次粒子纤维壁的有效导热系数，建立有效导热系数关于材料孔隙率、分形维数以及气固导热系数的函数关系式。

(2)基于硬硅钙石二次粒子壳体表面纤维及孔隙微尺度电镜扫描照片，采用差分盒维数算法，得到纤维的分布符合分形特征，并计算了材料的分形维数，结合材料的孔隙率，较为精确地描述了材料的微观空间结构。

(3)硬硅钙石二次粒子纤维壁的有效导热系数不仅与材料固相的自身性能有关，还与其内部的微尺度空间结构(纤维的分布、孔隙率)、材料的使用温度等因素相关。

[1] 陈小佳. 超轻硬硅钙石的制备和性能研究[D]. 武汉: 武汉理工大学材料学院, 2007.

[2] 苏高辉, 杨自春, 王洪宇. 微孔硅酸钙的有效导热系数和最佳使用密度[J]. 应用能源技术, 2011,4: 1-5.

[3] 郁伯铭. 多孔介质输运性质的分形分析研究进展[J]. 力学进展, 2003, 33(3): 333-346.

[4] Yongjin Feng, Boming Yu, Mingqing Zou, Duanming Zhang. A generalized model for the effective thermalconductivity of porous media based on self-similarity[J]. Appl. Phys, 2007, 37: 3030-3040.

[5] 王唯威, 淮秀兰. 分形多孔介质导热数值模拟分析[J]. 工程热物理学报, 2007, 28(5): 835-837.

[6] 施明恒, 李小川,陈永平. 利用分形方法确定聚氨酯泡沫塑料的有效导热系数[J]. 中国科学E, 2006, 36(5): 560-568.

[7] 徐 平, 杨 昆, 于英华. 泡沫铝微结构的分形特征及与孔隙率的关系研究[J]. 材料导报B, 2011, 25(11): 140-143.

[8] 阚安康, 韩厚德, 汤 伟.基于分形理论的开孔聚氨酯泡沫等效导热系数研究[J]. 材料导报B, 2012, 26(2): 143-146.

[9] Dathe A, Thullner M. The relationship between fractal properties of solid matrix and pore space in porous media[J]. Geoderma, 2005, 129(3-4): 279.

[10] Hunt A G. Basic transport properties in natural porous media: Continuum percolation theory and fractal model[J]. Complexity, 2005, 10(3): 22.

[11] Y S Touloukian, P E Livey, S C Saxena. Thermal conductivity: nonmetallic solids. New York: IFI/Plenum press, 1970.

[12] 魏高升. 纳米孔超级绝热材料的热物性研究[D]. 北京:北京科技大学机械工程学院, 2006.