CC板通道入口效应对传热特性和阻力特性的影响
魏晓阳,王利民,邓磊,车得福
(西安交通大学动力工程多相流国家重点实验室,陕西 西安 710049)
CC板通道入口效应对传热特性和阻力特性的影响
魏晓阳,王利民,邓磊,车得福
(西安交通大学动力工程多相流国家重点实验室,陕西 西安 710049)
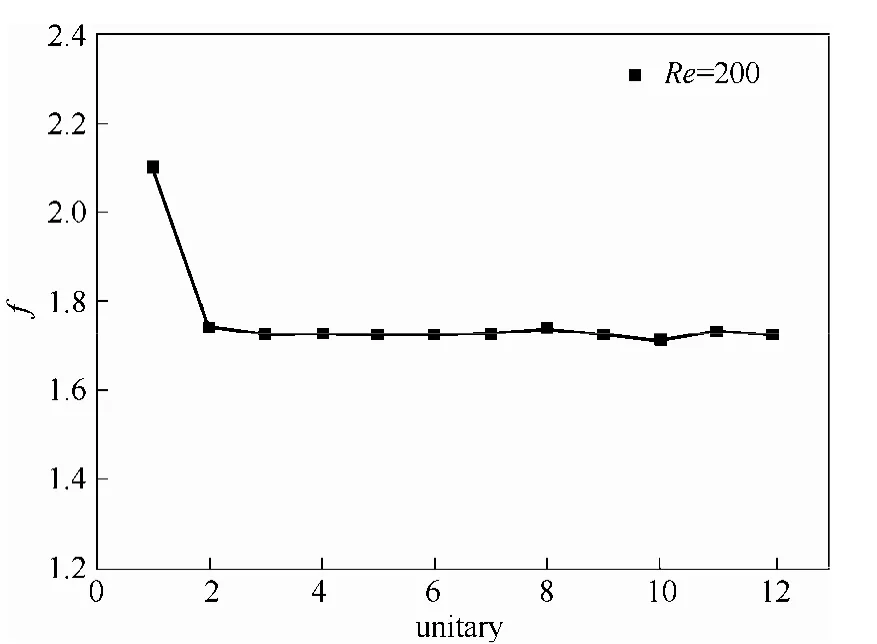
选取低Reynolds数k-ε湍流模型,采用数值模拟的方法计算了不同Reynolds数下入口效应和CC板通道单元体传热特性、阻力特性的关系。数值模拟的结果表明:入口效应的存在使得CC板通道前3个单元体的湍流强度显著变大,在第4个单元体之后入口效应对传热特性的影响可以忽略;随着Reynolds数的增加,由于CC板通道入口处湍流强度增加的程度逐渐变小,入口效应对传热效果的强化能力下降;随着Reynolds数的增加,入口段和充分发展段的摩擦阻力系数均有所下降;此外,由于入口效应的存在,CC板通道入口段的摩擦阻力系数比充分发展段高20%左右。
CC板通道;入口效应;传热;数值模拟;湍流强度;摩擦阻力系数
引 言
CC(cross corrugated)波纹板是一种典型的表面换热元件[1],如图1所示。CC板采用起伏的曲壁面诱发二次流动,二次流动则会破坏近壁边界层从而实现强化换热[2-3]。CC板具有良好的传热特性、阻力特性和较低的制造成本,因而广泛应用于回转式空气预热器和微型燃气轮机回热器[4-5]。
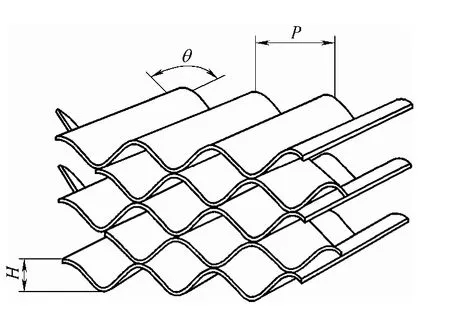
图1 CC板通道Fig.1 CC plate channel
目前国内外对CC板传热特性和阻力特性的研究十分充分。Focke等[6]和Ayub[7]对正弦形CC通道内的流动传热进行了全面、深入的研究,分析了不同结构参数对流动和换热的影响。Stasiek等[8]和Dović等[9]采用热色液成像技术对正弦形CC壁面上Nu分布进行了测量,研究了Reynolds数对流动和传热的影响。Gaiser[10-11]在实验中较为详细地研究了节高比、交错角对CC板整体和局部流动传热性能的影响。Kovalenko等[12]整理了100 尽管 Ciofalo 等[15]、Sundén 等[20-21]成功预测了CC板通道中入口效应的存在,但是多数学者也仅仅是以入口效应的存在来说明数值模型预测的结果符合CC板入口处的实际流动情况,而学者们主要着眼于CC板通道内流动充分发展后的传热特性和阻力特性,并在此基础上提出了流动充分发展段Nu和f的拟合关联式。 目前学者们很少关注入口效应对传热特性、阻力特性的影响,相应的理论分析也有待于进一步完善。鉴于此,本文研究了入口效应对CC板通道传热特性、阻力特性的影响。与以往学者相比,在对比入口效应对传热特性、阻力特性影响的基础上,分析了CC板通道产生入口效应的深层原因,具有重要的理论意义。 CC板通道结构如图1所示,通道形状由上下交错的正弦波纹板确定,其中波纹节距(周期)为P,振幅为 H/2,波纹板交错角为 θ。采用 Ciofalo等[15]提出的单元体的概念,数值计算在单元体内进行。 CC板通道上下两板接触点的组成部分为一个单元,单元体的结构如图2所示,分别有两股流体的入口和出口,上下波纹板的交错角为 60°,波纹节距P=2.36 mm,波纹高度H=2.14 mm,其中单元体沿主流方向长度为4.08 mm,单元体宽度为2.36 mm。 图2 单元控制体Fig.2 Unitary cell Sundén等[20-21]将层流模型(LAM)、标准 k-ε模型(SKE)和低Reynolds数k-ε湍流模型(LBKE)[22]的数值模拟结果和实验结果进行了对比,发现LBKE模型能准确反映入口效应的影响。因此,采用LBKE模型研究CC板通道的入口效应。 数值模拟中采用如下的假设: (1)流体为不可压缩的牛顿流体; (2)流体在通道中处于稳定流动状态; (3)忽略壁面的导热; (4)不考虑重力场的影响; (5)流体进口速度给定,来流温度为300 K,出口压力为1个标准大气压。 基于上述假设,描述本物理问题的连续性方程、动量方程和能量方程分别为 压力和速度耦合采用SIMPLEC算法[23],对控制方程离散时,扩散项采用中心差分格式、对流项采用二阶迎风格式。数值计算过程中对残差、速度、温度和出口压力连续监测以判断计算是否收敛[24]。 CC板通道内工作介质为空气,流体有两股进口和出口,如图2(a)所示,沿主流方向进口的速度和温度给定,出口处压力给定(1个标准大气压);垂直于主流方向的进口和出口按充分发展处理,即进出口流体的温度、速度及压力完全相同;CC通道的上下表面为无滑移边界条件;空气预热器表面热通量范围为 1000~2000 W·m-2[25],取 q=1500 W·m-2。 传热特性是指单元体壁面将热量传递给流体工质的能力,这种能力用量纲1数Nu衡量。阻力特性是指流体工质在流经单元体通道过程中所产生的阻力的大小,用摩擦阻力系数f来衡量。本研究所用参数的定义如下: (1)当量直径 (2)Reynolds数 (3)摩擦阻力系数 (4)平均Nusselt数 针对 CC板通道入口效应的研究,采用ICEM-CFD生成非结构化网格[26],网格分布非均匀,在进出口处网格较密,在单元体中间部分网格较疏,以便有效地求解近壁面处较大的温度和压力梯度[27]。CC板通道计算区域结构和网格如图3所示。 获得网格独立解是判断数值计算是否合格的基本标准[28]。为了消除网格疏密变化引起的数值误差,在正式计算之前需要对计算区域的网格进行独立性验证。采用6个不同的网格数进行了数值计算,Re=1000时求得平均 Nusselt数随网格数的变化趋势,如图4所示。 图3 CC通道模型和网格Fig.3 Model and grid of CC plate 图4 网格独立性Fig.4 Grid independence 计算结果表明当网格数达到 524886以上时,Nu趋于一定值,数值计算的结果不再随着网格的加密而发生明显变化。因此,本研究中网格数量为524886个。 采用Utriainen等[4]给出的CC2.2-60正弦波纹通道模型。为了和CC2.2-60正弦波纹通道模型的实验结果对比,Re的选取范围为200~1500。 对计算区域入口段表面平均 Nusselt数进行了数值计算,并和Utriainen等[4]在文献中给出的实验数据对比。图5为数值计算结果和实验结果的对比,可见两者吻合较好,充分说明了计算方法的准确性。 图5 平均Nu实验值与模拟值的比较Fig.5 Comparison between tested Nu and those obtained by simulation 图6为Re=200时入口效应对换热效果的影响。其中,纵坐标Nu/Nu5为各个单元体的Nusselt数与单元体5的Nusselt数之间的比值,Nu/Nu5用来衡量入口处单元体传热的强化能力。 图6 Re=200时入口效应和换热的关系Fig.6 Relationship between entrance effect and heat transfer when Re=200 由图6可以看出,入口效应对传热的强化在单元体1处非常明显,在单元体2和单元体3处的传热强化效果逐渐减弱,在单元体4中入口效应对换热影响非常微小,在单元体5中入口效应对传热的影响基本可以忽略。即沿着主气流方向入口效应对传热的强化逐渐减弱,在单元体4之后流体已达到充分发展状态。 根据流体力学的基本原理[29],当流体与管壁之间有热交换时,管子壁面上的热边界层有一个从零开始增长直到汇合于管子中心线的过程。入口段的湍流强度较大,热边界层较薄,因此局部表面传热系数比充分发展段高,且沿着主流方向逐渐降低。 如图6所示,前3个单元体的传热系数逐渐下降,这是因为湍流强度逐渐减小、热边界层沿主流方向逐渐变厚导致;而单元体4的传热系数略高于单元体 3,这是因为随着边界层厚度的增加,热边界层中开始逐渐出现湍流,湍流的扰动与混合作用又会使局部传热系数有所提高;在单元体4之后,湍流的扰动和混合作用逐渐趋于稳定,热边界层厚度也趋于定值,因此在单元体4之后流体已达到充分发展状态。 图7 不同单元体出口湍流强度分布(Re=200)Fig.7 Distribution of turbulent intensity in outlet of different units (Re=200) 入口效应对CC板通道传热强化的主要原因是在入口处湍流强度的增加。湍流强度是衡量脉动速度对平均速度的偏离程度。以Re=200为例,图7展示了计算区域各单元体出口面上的湍流强度分布。可以看出,单元体1出口截面上湍流强度明显较大,边界层较薄,换热效果较好;单元体2和单元体3出口截面上的湍流强度逐渐下降,边界层厚度逐渐增加,换热效果变差;单元体 4、单元体 5和单元体6湍流强度的分布基本相同,边界层厚度也基本相同,换热效果趋于稳定。因此可以认为单元体4以后流体已达到充分发展状态。这也和前述结果是吻合的。 为了进一步研究入口效应和Re的关系,分别计算了Re=200、500和1000时入口效应对单元体传热效果影响,如图8所示。 图8 不同Reynolds数下入口效应对传热的影响Fig.8 Influence of entrance effect on heat transfer in different Reynolds numbers 由图8可以看出:不同Reynolds数下单元体3的Nu/Nu5值均小于单元体4。这是因为在单元体3和单元体4之间,沿主流方向随着边界层厚度的增加,热边界层中开始逐渐出现湍流,湍流的扰动与混合作用又会使局部传热系数有所提高。所以出现了单元体3的Nu/Nu5值小于单元体4的现象。 随着Re的增大,入口效应对传热的影响逐渐减弱。Re=200时,单元体1的传热效果比充分发展段提高了约28%左右。当Re逐渐增大至500和1000时,单元体1的传热效果分别提高了13%和7%。即随着Re的增加,CC板通道入口处第1个单元体的传热强化效果逐渐下降。 根据前文分析,入口段换热效果显著增强的原因是入口段单元体中湍流强度的增加。为了衡量入口段湍流强度相对于充分发展段的增加程度,表1列举了不同Reynolds数下的单元体1和单元体5各自的湍流强度,其中l1/l5为单元体1和单元体5湍流强度的比值。 表1 不同Reynolds数下CC板通道的湍流强度Table 1 Turbulent intensity of CC plate channel in different Reynolds numbers 由表1可以看出,Re=200、500和1000时,l1/l5分别为9.36、4.98和4.32。这表明随着Re的变大入口效应对第 1个单元体传热的强化能力逐渐下降。即尽管低Reynolds数时传热效果较低,但入口效应的强化效果明显;而Reynolds数较高时,传热效果较好,入口效应对传热的强化不明显。 出现上述现象的原因是:低Reynolds数时入口附近单元体湍流强度的增加程度明显。根据前文分析,CC板通道在第5个单元体中已达到充分发展状态,因此以第 5个单元体的湍流强度(l5)为基准,分别计算了各个单元体湍流强度(l)与l5的比值,如图9所示。 图9 不同Reynolds数下l/l5的变化趋势Fig.9 Variation tendency of l/l5 in different Reynolds numbers 由图9可以看出:沿着主流方向,l/l5逐渐减小;在第4个单元体之后l/l5保持为定值,这也说明入口效应提高了前4个单元的湍流强度,因此强化了前 4个单元的传热效果。各单元体l/l5的变化趋势和图8中Nu/Nu5的变化趋势基本相同,因此,各单元体湍流强度的变化可反映相应的传热效果。 阻力损失是CC板通道的另一个重要参数,文中采用达西摩擦阻力系数f衡量阻力损失的大小[30]。入口效应在强化单元体传热的同时,也会使得流体流经单元体时的阻力系数f有所增加。 图10为Re=200时计算区域内各单元体摩擦阻力系数f的大小。可以看出,入口效应只影响第 1个单元体的摩擦阻力系数,在第2个单元体之后摩擦阻力系数基本趋于定值。因此,在Re=200时,入口效应只影响CC板通道入口段第1个单元体的摩擦阻力系数。 图10 Re=200时各单元体的摩擦阻力Fig.10 Friction of unitary cell when Re=200 为了衡量不同Reynolds数下入口效应对CC板通道摩擦阻力的影响程度,以充分发展段单元体 3的摩擦阻力系数作为基准,分别计算了不同单元体与单元体3摩擦阻力系数的比值f/f3,如图11所示。 图11 不同Reynolds数下f/f3的变化趋势Fig.11 Variation tendency of f/f3 in different Reynolds numbers 由图11可以看出:当Re=200、500和1000时,f/f3的变化趋势基本相同,并且入口段(单元体1)的摩擦阻力系数相对于充分发展段(单元体2之后)增加了约20%。这说明不同Reynolds数下入口效应对 CC板通道入口段摩擦阻力的影响程度基本相同。因此,在不同Reynolds数下,若CC板通道充分发展段的摩擦阻力系数已知,即可预测入口段的摩擦阻力系数。 通过上文分析得出:CC板通道入口效应的存在对各单元体内的传热和阻力有明显的影响。以下从传热和阻力特性来阐述分析CC板单元体内的流动情况。 对于第 1、2个单元体,入口效应的存在强化了单元体内湍流流动,使得单元体内的湍流强度明显变大。因此前两个单元体的换热明显变好,但同时也会使得入口段单元体的阻力变大。 对于第3个单元体,尽管入口效应也会使得湍流强度变大,但是由于沿着主流方向边界层厚度逐渐发展,所以第3个单元体换热效果反而有所恶化,而工质流动的阻力系数已基本不再发生变化。 对于第4个单元体,在边界层厚度增长至湍流流动的边界之后,湍流的扰动作用使得边界层厚度变薄,传热效果好于第3个单元体,但此时工质的流动阻力系数已基本不再发生变化。 对于第5个单元体之后,流动边界层和热边界层已经不再发生明显变化,工质流动已达到充分发展阶段。因此,Nu和阻力系数f基本达到定值。 模拟了不同Reynolds数下入口效应对CC板通道传热和阻力特性的关系,针对上下波纹板交错角为60°、波纹节距P=2.36 mm和波纹高度H=2.14 mm的CC板,分别得到了如下结论: (1)入口效应可以强化CC板通道的传热效果。对于CC板通道,入口效应的存在使得前4个单元体的湍流强度显著变大,在第4个单元体之后入口效应对传热的影响可以忽略。 (2)随着Reynolds数的增加,入口效应对传热效果的强化能力下降。这主要是因为Reynolds数较高时入口段湍流强度的增加程度变小,因此,入口效应强化传热的能力逐渐下降。 (3)随着Reynolds数的增加,入口段和充分发展段的摩擦阻力系数均有所下降。 (4)入口效应对CC板通道摩擦阻力的影响仅体现在第1个单元体上。当Reynolds数不同时,第1个单元体的摩擦阻力相对于充分发展段均增加了约20%。 符 号 说 明 A——单元体截面面积,mm cp——流体比定压热容,J·kg-1·K-1 Dh——当量直径,mm f——摩擦阻力系数 H——CC板波纹高度,mm L——主流方向单元体长度,mm l——湍流强度 Nu——Nusselt数 P——CC板波纹节距,mm Pj——单元体截面周长,mm Pr,Prt——分别为层流和湍流Prandtl数 p——压力,Pa Δp——单元体进出口截面压力差,Pa q——热通量,W·m-2 〈qw〉 ——平均壁面热通量,kJ·m-2 Re——Reynolds数 T——流体特征温度,K Tf——流体体积平均温度,K Tw——单元体壁面平均温度,K U——特征速度,m·s-1 u——单元体中流体速度,m·s-1 x——坐标轴 θ——波纹板交错角,(°) λ——流体热导率,W·m-1·K-1 μ,μt——分别为层流黏度、湍流黏度,Pa·s ρ——流体密度,kg·m-3 下角标 i,j——张量下标 [1] ROBSON N C, HELEN B S, DONACHIE A M,et al. Numerical investigation of flow field and heat transfer in cross-corrugated ducts[J]. Journal of Heat Transfer, 1999, 121(2): 314-321. [2] MULEY A, MANGLIK R M. Experimental study of turbulent flow heat transfer and pressure drop in a plate heat exchanger with chevron plates[J]. Journal of Heat Transfer, 1999, 121(1): 110-117. [3] MEHRABIAN M A. Hydrodynamics and thermal characteristics of corrugated channels: computational approach[J]. Experimental Heat Transfer, 2000, 13(3): 223-234. [4] UTRIAINEN E, SUNDÉN B. Evaluation of the cross corrugated and some other candidate heat transfer surfaces for microturbine recuperators[J]. Journal of Engineering for Gas Turbines & Power,2002, 124(3): 550-560. [5] BABU T P A, TALEKALA M S. Evaluation of heat transfer surfaces for compact recuperator using a CFD code[J]. Heat & Mass Transfer,2009, 45(6): 767-774. [6] FOCKE W W, ZACHARIADES J, OLIVIER I. The effect of the corrugation inclination angle on the thermohydraulic performance of plate heat exchangers[J]. International Journal of Heat and Mass Transfer, 1985, 28(8): 1469-1479. [7] AYUB Z H. Plate heat exchanger literature survey and new heat transfer and pressure drop correlations for refrigerant evaporators[J].Heat Transfer Engineering, 2003, 24(5): 3-16. [8] STASIEK J, COLLINS M W, CIOFALO M,et al. Investigation of flow and heat transfer in corrugated passages (Ⅰ): Experimental results[J]. International Journal of Heat and Mass Transfer, 1996,39(1): 149-164. [9] DOVIĆ D, SVAIC S. Influence of chevron plates geometry on performances of plate heat exchangers[J]. Tehnički Vjesnik, 2007,14(1Part2): 37-45. [10] GAISER G, KOTTKE V. Effects of corrugation parameters on local and integral heat transfer in plate heat exchangers and regenerators[C]// Proc. 9th Int. Heat Transfer Conference, 1990, (5):85-90. [11] GAISER G. Flow phenomena and local heat and mass transfer in corrugated passages[J]. Chemical Engineering & Technology, 1989,12(1): 400-405. [12] KOVALENKO L M, OBOLENTSEV Y G. Plate heat exchangers with complex shaped heat transfer surfaces and their design[J]. Chemical and Petroleum Engineering, 1974, 10(4): 315-319. [13] SAWYERS D R, SEN M, CHANG H C. Heat transfer enhancement in three-dimensional corrugated channel flow[J]. International Journal of Heat & Mass Transfer, 1998, 41(22): 3559-3573. [14] YANG Y T, CHEN P J. Numerical simulation of fluid flow and heat transfer characteristics in channel with V corrugated plates[J]. Heat &Mass Transfer, 2010, 46(4): 437-445. [15] CIOFALO M, STASIEK J, COLLINS M W. Investigation of flow and heat transfer in corrugated passages (Ⅱ): Numerical simulations[J].International Journal of Heat and Mass Transfer, 1996, 39(1):165-192. [16] ZHANG L, CHE D F. Turbulence models for fluid flow and heat transfer between cross-corrugated plates[J]. Numerical Heat Transfer Part A-Applications, 2011, 60(5): 410-440. [17] 阴继翔, 李国君, 丰镇平. 交错波纹板原表面换热器通道内对流换热的数值研究[J]. 西安交通大学学报, 2005, 39(1): 36-40.YIN J X, LI G J, FENG Z P. Numerical study on the characteristics of convection heat transfer in crossed-corrugated primary surface exchanger[J], Journal of Xi’an Jiaotong University, 2005, 39(1):36-40. [18] 李国君, 阴继翔, 丰镇平. CC型通道波纹相对节距对流动与换热特性的影响[J]. 动力工程, 2005, (4): 567-572.LI G J, YIN J X, FENG Z P. Effects of pitch-to-height ratio on flow and heat transfer characteristics in cross-corrugation passages[J].Journal of Power Engineering, 2005, (4): 567-572. [19] 聂嵩, 曲伟. CC型原表面换热器传热与流动数值模拟[C]//中国工程热物理学会传热传质学学术会议, 2003.NIE S, QU W. Numerical simulation of heat transfer and flow of CC type primary surface heat exchange[C]// Academic Conference on Heat and Mass Transfer in Chinese Society of Engineering Thermophysics, 2003. [20] ETEMAD S, SUNDÉN B, ETEMAD S. CFD-analysis of fully developed turbulent flow and heat transfer in a unitary cell of a cross corrugated plate pattern heat exchanger[C]// ASME/JSME 2007 Thermal Engineering Heat Transfer Summer Conference Collocated with the ASME 2007 InterPACK Conference, 2007. [21] SUNDÉN B. Computational fluid dynamics in research and design of heat exchangers[J]. Heat Transfer Engineering, 2007, 28(11):898-910. [22] LAM C K G, BREMHORST K. A modified form of the k-epsilon model for predicting wall turbulence[J]. ASME Transactions Journal of Fluids Engineering, 1981, 103(3): 456-460. [23] VANDOORMAAL J P, RAITHBY G D. Enhancements of the simple method for predicting incompressible fluid-flows[J]. Numerical Heat Transfer, 1984, 7(2): 147-163. [24] PATANKAR S V. Numerical Heat Transfer and Fluid Flow[M].Hemisphere Pub. Corp., 1980: 125-126. [25] CHEW P E. Rotary air preheaters on power-station boilers[R].Central Electricity Generating Board, Southampton (UK), Technology Planning and Research Div., 1985. [26] 武利龙, 陈斌. 基于气泡堆积的非结构化网格生成技术[J]. 西安交通大学学报, 2009, (1): 29-33.WU L L, CHEN B. Bubble packing method based unstructured grid generation[J]. Journal of Xi’an Jiaotong University, 2009, (1): 29-33. [27] ZHANG L, CHE D F. Influence of corrugation profile on the thermalhydraulic performance of cross-corrugated plates[J].Numerical Heat Transfer Part A-Applications, 2011, 59(4):267-296. [28] 陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2003: 32.TAO W Q. Numerical Heat Transfer[M]. Xi’an: Xi’an Jiaotong University Press, 2003: 32. [29] 张鸣远, 景思睿, 李国君. 高等工程流体力学[M]. 北京: 高等教育出版社, 2012: 232.ZHANG M Y, JING S R, LI G J. Higher Engineering Fluid Mechanics[M]. Beijing: Higher Education Press, 2012: 232. [30] 杨世铭, 陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社, 1998:244.YANG S M, TAO W Q. Heat Transfer[M]. 4th ed. Beijing: Higher Education Press, 1998: 244. date:2017-01-19. CHE Defu, dfche@mail.xjtu.edu.cn supported by National Key Technology Research and Development Program of the Ministry of Science and Technology of China (2015BAA04B02). Influence of entrance effect of CC plate channel on thermal and hydraulic characteristic WEI Xiaoyang, WANG Limin, DENG Lei, CHE Defu The influence of entrance effect on thermal and hydraulic characteristics for CC plate channel was numerically studied by adopting the lower Reynoldsk-εturbulence flow model. The simulation results indicated that the entrance effect significantly enhanced turbulent intensity at the first three unitary cells and the influence of entrance effect on heat transfer could be neglected after the fourth unitary cell. Because the increase of turbulent intensity in the inlets reduces with increasing Reynolds number, the heat transfer enhancement could be depressed.As the Reynolds number increases, the friction coefficients of entrance and fully developed section both decrease.In addition, the friction coefficient of inlet section is approximately 20% higher than that of fully developed section. CC plate; entrance effect; heat transfer; numerical simulation; turbulence intensity; friction coefficient TK 02 A 0438—1157(2017)11—4061—08 10.11949/j.issn.0438-1157.20170090 2017-01-19收到初稿,2017-07-12收到修改稿。 联系人:车得福。 魏晓阳(1993—),男,博士研究生。 国家科技支撑计划项目(2015BAA04B02)。1 模型描述
1.1 物理问题描述
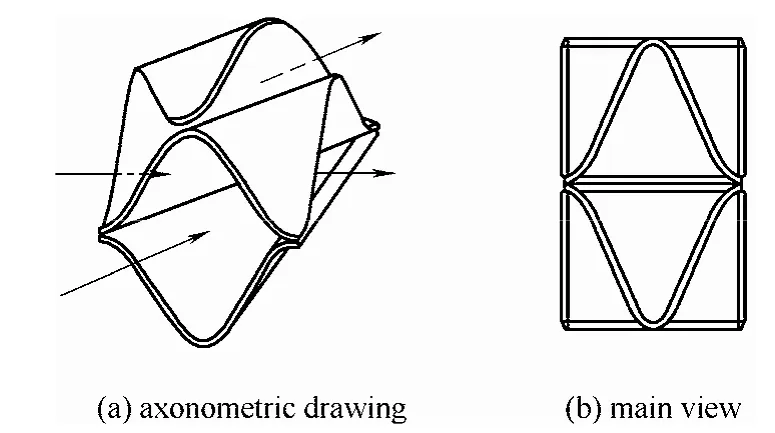
1.2 数值模型

1.3 边界条件
1.4 性能参数




2 网格独立性及模型验证
2.1 网格独立性


2.2 模型验证

3 结果与分析
3.1 入口效应和换热效果的关系
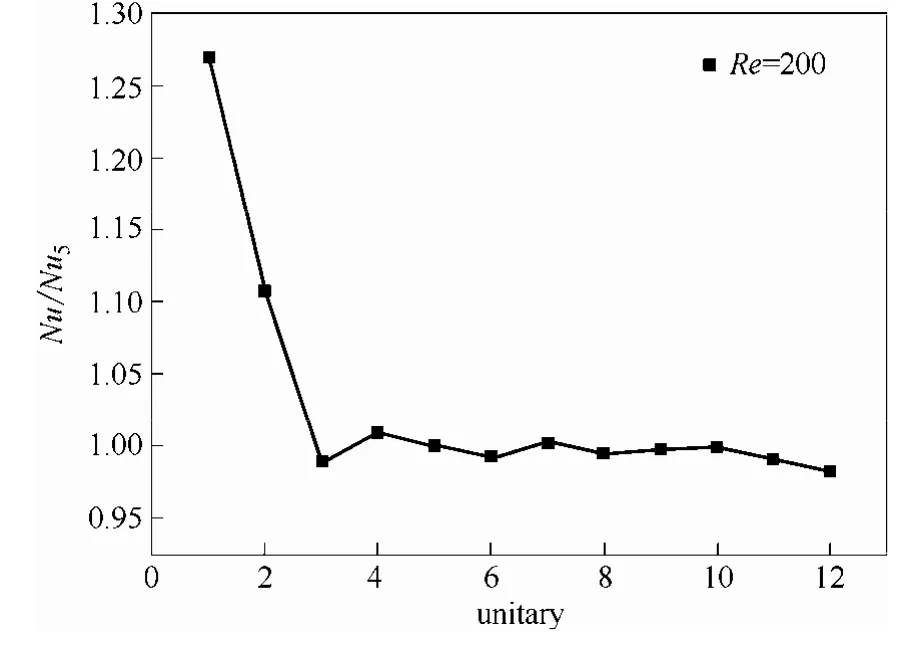

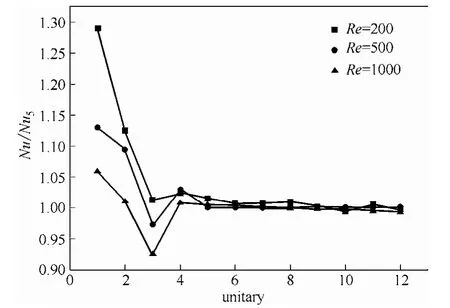


3.2 入口效应和摩擦阻力的关系

3.3 单元体流动情况
4 结 论
(State Key Laboratory of Multiphase Flow in Power Engineering,Xi’an Jiaotong University,Xi’an710049,Shaanxi,China)

