结合PCA的SVM方法在学校财务风险预警中的运用

淦 艳 魏 延 杨 有

(重庆师范大学计算机与信息科学学院， 重庆 401331)

0 前言

自20世纪90年代Vapnik等人提出支持向量机(Support Vector Machine, SVM)以来,支持向量机已经在手写识别、语音识别、人脸识别和文本分类等工作中得到了广泛应用[1-2]。Jae Joon Ahn等人将支持向量机方法应用于早期预警系统，提出针对金融危机利用支持向量机开发一种早期预警系统的实用性[3]。Jae H Min等人将支持向量机方法用于破产预测，提出使用支持向量机核函数参水最优选择的破产预测，通过实验验证支持向量机方法的预测精度优于多元判别分析，Logistic回归分析和神经网络[4]。随着社会经济的发展，支持向量机也在经济研究领域中得到更多应用。但是目前SVM在财务风险预警中的应用远不如手写识别、人脸识别和文本分类那么广泛。

本文将支持向量机方法运用于经济领域中的财务风险预警，利用所建模型，通过中职学校的具体数据进行实例验证。支持向量机方法在学校财务风险预警中具有可行性和实用性，预测精度较高，能够较为准确地预测学校在未来某一年的财务风险，从而为领导层提供决策参考。

1 财务风险预警评价指标的选取

财务风险预警的分析需要考虑多个方面的因素。

文献[5]通过资金周转、资金分配、资金运用和主题连带风险等4类9个指标研究了高等学校财务预警系统；文献[6]通过偿债能力、运营能力和成长能力3类20个指标研究了高校财务风险预警；文献[7] 通过偿债能力、盈利能力、营运能力、成长能力、现金流量和规模6类25个指标研究了上市公司财务预警；文献[8] 通过偿债能力、营运能力、获利能力、成长能力、财务结构和现金流量6类15个指标研究了上市公司财务危机预警；文献[9]通过盈利能力、资产流动性、负债管理能力、运营能力、现金生产能力、经营发展能力、资本市场表现和风险水平8类28个指标研究了中国医药制造企业财务危机预警；文献[10] 通过从短期偿债能力、长期偿债能力、资本结构、营运能力、获利能力、投资报酬能力、成长能力和现金流量8类38个指标研究了财务危机预警；文献[11]通过偿债能力、营运能力和发展潜力3类9个指标研究了高等院校财务风险管理。本次研究受文献[5] — [11]提出的评价指标的启发，结合中职学校自身的特点，主要从偿债能力、营运能力、成长能力和发展潜力4大类22个评价指标去分析，判断学校是否存在财务风险。

通过对文献[5] — [11]的研究，发现现实支付能力、潜在支付能力、资产负债率、收入负债率、流动比率、收入支出比率、净资产收入比率、学校债务率、总资产周转率、收入支出平衡比率、净增长率、资产增长率、自有资金余额占年末货币资金的比重、自有资金净余额占年末货币资金的比重、非自有资金余额占年末货币资金的比重、总资产增长率、资本积累率、师生比、生均事业支出、生均校舍面积、生均占地面积和教师人均科研经费，共计22个指标是他们所采用过的预警指标，说明了这些指标的重要性，因此这些指标在我们的预警系统中均予以采用。同时结合学校的实际情况，本文选用上述22个指标，并分成4大类，通过指标变化评价某中职学校是否存在财务风险。

试验数据均来源于重庆某中职学校1993年到2012年间具体的财务数据和学校其他相关数据(占地面积、师生人数、校舍面积)。

1.1 偿债能力评价指标

企业的偿债能力是指企业用其资产偿还长期债务与短期债务的能力。根据学校实际情况，提出了5个偿债能力评价指标，具体评价指标所用符号、评价指标名称及计算方法如表1所示。

表1 偿债能力评价指标

1.2 营运能力评价指标

营运能力是指企业的经营运行能力，即企业运用各项资产以赚取利润的能力。根据学校实际情况，提出了5个营运能力评价指标，具体评价指标所用符号、评价指标名称以及计算方法，如表2所示。

1.3 成长能力评价指标

企业成长能力是指企业未来发展趋势与发展速度，包括企业规模的扩大、利润和所有者权益的增加。根据学校实际情况，提出了7个成长能力评价指标，具体评价指标所用符号、评价指标名称及计算方法如表3所示。

1.4 发展潜力评价指标

发展潜力是衡量一个企业的未来是否具有发展空间，根据学校实际情况，提出了5个成长能力评价指标，具体评价指标所用符号、评价指标名称及计算方法如表4所示。

2 财务风险预警的方法

本文对财务风险预警研究的方法包括主成分分析(Principal Components Analysis, PCA)和支持向量机(Support Vector Machine, SVM)。

表2 营运能力评价指标

其中，主成分分析(Principal Components Analysis, PCA)是统计分析中一种分析、简化数据集的技术。它经常用于减少数据集的维数，同时保持数据集对方差贡献最大的特征。这是通过保留低阶主成分，忽略高阶主成分而实现，这样低阶成分往往能够保留住数据的最重要方面。该分析法由卡尔·皮尔逊于1901年提出，用于分析数据及建立数理模型，主要通过对协方差矩阵进行特征分解，以得到数据的主成分(即特征矢量)及其权值。通过上述分析，提出了22个评价指标。这22个评价指标之间存在一定的耦合关系，为了降低评价指标之间的耦合性和节约运行时间，首先使用主成分分析(Principal Components Analysis, PCA)对输入数据进行处理，从而降低原来评价指标之间存在的耦合性并减少数据维数。

表3 成长能力评价指标

表4 发展潜力评价指标

支持向量机(SVM)法是通过一个非线性映射，将输入映射到一个高维特征空间中，在特征空间中寻求一个最优分类面，使得原始的非线性问题在特征空间中线性可分。财务风险预警实际上是一个非线性问题，假定有n个样本的训练集

T={(φ(x1),y1),(φ(x2),y2),…,

(φ(xi),yi),…,(φ(xn),yn)}

(1)

其中i=1,2,…,n，φ(xi)是xi从Rn到Hilbert空间的映射，φ(xi)∈H，H是Hilbert空间，yi∈{-1,1}。若yi=+1时，代表中职学校财务状态良好；反之，yi=-1时，代表学校出现财务危机。在此引入松弛变量ξi目标函数：

s.t.yi((w·φ(xi))+b)≥1-ξi,ξi≥0,
i=1,2,…,n

(2)

在支持向量机中升维是通过非线性映射来实现。根据泛函理论，在高维特征空间中只需要进行内积运算，而这种内积运算是可以用原空间中的函数实现的，不必知道变换的具体形式，即φ(xi)并不清楚其具体表达形式，φ(xi)·φ(x)无法进行计算。为此引入核函数，只要一个核函数满足Mercer条件,它就对应某一个变换空间的内积，在最优分类面中采用合适的内积函数就可以实现非线性变换后的线性分类。假定核函数：

K(xi,xj)=φ(xi)·φ(xj)

(3)

经过推导，可以得到最优分类函数

(4)

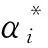
(5)

3 实验分析

根据上述22项评价指标及重庆某中职学校的实际财务数据，计算出22个评价指标的值，运用PCA方法处理之后作为SVM的输入数据。运行环境：处理器Intel(R) Core(TM) i3-2250M cpu @ 2.30GHz，内存为4.00GB，MATLAB版本为matlab R 2012 b。

在评价指标的选取中，其中有些评价指标所起的作用不大，因此首先运用主成分分析法对评价指标进行降维处理。选取的不同主成分个数对应不同的累计贡献率，表5给出了从1到10对应累计贡献率的大小。

表5 评价指标主成分累计贡献率

从表5清楚地看到，前7个主分量的累计贡献率为0.846 9，小于文献[12]、[13]中给出的最小值0.85，然而前8个主分量的累计贡献率为0.891 8，已经超过0.85，即前8个主分量在整个数据分析中占有绝对重要的比重，因此选取前8个主分量为支持向量机的输入数据，从而有效地对原来的22个评价指标进行降维。

libsvm工具箱是一套简单易用的SVM模式识别和回归机软件包，因此，在实验时运用libsvm软件，使用默认的RBF核函数，用交叉验证方法寻找最佳的惩罚因子C和核函数中的方差g，然后利用最佳的参数训练模型。

实验假设：若用“+1”代表学校财务状态良好，反之，用“-1”代表学校出现财务危机。从20组数据中随机抽取10组数据用来做训练数据集，其余10组(或是用20组数据来做预测)数据用来做测试集。

从表6中前4组可以得知：当用10组做测试数据的时候，最高测试分类精度达到100%，最低测试分类精度为80%，平均测试分类精度为92.5%；当用20组做测试数据的时候，最高的测试分类精度达到95%；就实验结果整体而言平均测试分类精度为93.75%。从预测学校财务风险的角度分析，有93.75%的预测精度，说明预测能力较强，可信度高。这些数据验证了本文提出的评价指标合理性，以及主成分分析方法和支持向量机方法在财务风险预警中的可行性。

表6 训练集分类精度和测试集分类精度表

4 结 语

支持向量机有坚实的理论基础，其分类应用十分广泛。本次研究使用支持向量机方法，将其应用于学校财务风险预警中，预测学校在未来是否存在财务风险。研究中结合学校的具体情况，提出了22个评价指标，并给出了相应的计算方法；然后利用PCA对获得的数据进行降维处理，最后通过实验得到的平均预测精度为93.75%，即对学校未来是否存在财务风险有93.75%的预测准确率。验证了提出的评价指标的合理性，以及主成分分析方法和支持向量机方法在财务风险预警中的可行性和实用性。

[1] Cortes C,Vapnik V.Support-Vector Networks[J].Machine Learning,1995,20:273-297.

[2] 胡哲,郑诚,闵鹏鹏.支持向量机及其应用研究[J].重庆科技学院学报：自然科学版,2008,10(2):121-124.

[3] Jae Joon Ahn,Kyong Joo Oh,Tae Yoon Kim,et al.Usefulness of Support Vector Machine to Develop an Early Warning System for Financial Crisis[J].Expert Systems with Applications,2011,38:2966-2973.

[4] Jae H.Min,Young-Chan Lee.Bankruptcy Prediction Using Support Vector Machine with Optimal Choice of Kernel Function Parameters[J].Expert Systems with Applications,2005,28:603-614.

[5] 汪国安.高等学校财务预警系统的研究[D].上海:同济大学,2006.

[6] 曹慧.基于神经网络技术的高校财务风险预警研究[D].南京：东南大学,2008.

[7] 汪金.基于支持向量机原理的上市公司财务预警模型实证研究[D].武汉：华中科技大学,2007.

[8] 阎娟娟.基于支持向量机的上市公司财务危机预警研究[D]. 西安：陕西科技大学,2006.

[9] 杨涛.基于SVM的中国医药制造企业财务危机预警研究[D].厦门：厦门大学,2009.

[10] 王敏.基于粗糙集和支持向量机的财务危机预警模型研究[D].西安：西安电子科技大学,2011.

[11] 瓮建鹏.高等院校财务风险管理研究[D].河北：河北农业大学,2011.

[12] 陈浩文,陈勇,林海明.主成分分析应用中应注意的问题[J].统计与决策,2009(8):140-141.

[13] 蔡波,姚泽清,张倩.主成分分析法在分析江苏经济发展状况中的应用[J].数学的实践与认识,2008,38(11):7-16.