梯形不锈钢筛条堆拉系数数学模型的优化
王亚芹 刘欣玉 贾尚武
(1.安徽机电职业技术学院机械工程系,安徽 芜湖 241000;2.中国重型机械研究院股份公司,西安 710032)
在连轧过程中,为使连轧过程能够顺利进行,实际生产过程采用堆钢或者拉钢工艺,即张力轧制。一般在连轧机组与机组之间采用堆钢轧制,而机组内的机架与机架之间采用拉钢轧制[1]。
本文针对目前传统堆拉系数数学模型误差较大的弊端,提出了填充系数对堆拉系数的影响,建立了基于堆拉系数的优化改进后的堆拉系数数学模型,并借助于大型有限元软件ANSYSLS-DYNA,以梯形不锈钢筛条轧制工艺为例,验证优化后的数学模型。
1 堆拉系数数学模型的改进
如式(1)所示为传统堆拉系数数学模型,与连轧常数、前滑系数有关,一般情况下,假定连轧过程各机架连轧常数相等。

式中:ki—第i机架连轧时堆拉系数
Ci—连轧常数,C1=C2=C3=C4
vi—第i机架轧辊线速度
式(1)中未考虑填充系数的影响,因此,计算过程误差大,甚至会导致错误,因此,本文修正堆拉系数数学模型为:

式中,ηi—第i道次孔型填充系数
2 有限元模拟
2.1 有限元模型的建立
为验证文中改进后的堆拉系数数学模型的准确性,采用ANSYSLS-DYNA软件对4道次梯形不锈钢筛条连轧过程进行有限元模拟,分析了轧件连轧过程前滑系数、填充系数、堆拉系数参数,并与传统堆拉系数数学模型计算结果比较。
梯形筛鼓棒条产品规格为:坯料Φ3.3 mm的不锈钢圆棒,材质型号为E300,开轧速度为13 mmin,背宽2.2 mm,梯形角度9°。孔型示意图如图 1所示。

图1 孔型示意图
根据孔型图建立有限元模型,考虑到模型的对称性,为节约计算时间,取12为有限元模型(图2)。

图2 有限元模型
2.2 结果分析
研究公式(2)的准确性,获取与堆拉系数相关的参数,以便验证本文改进后的堆拉系数数学模型的准确性,图3所示为4道次连轧过程横截面形状。
选取轧件中的5个典型位置为研究对象,分别为 A、B、C、D、E,如图4 所示。
根据式(1)计算前滑系数(表1),获取轧件轧辊线速度与轧件实际轧制速度(图5)。

图3 4道次横截面示意图

图4 轧件典型位置点示意图
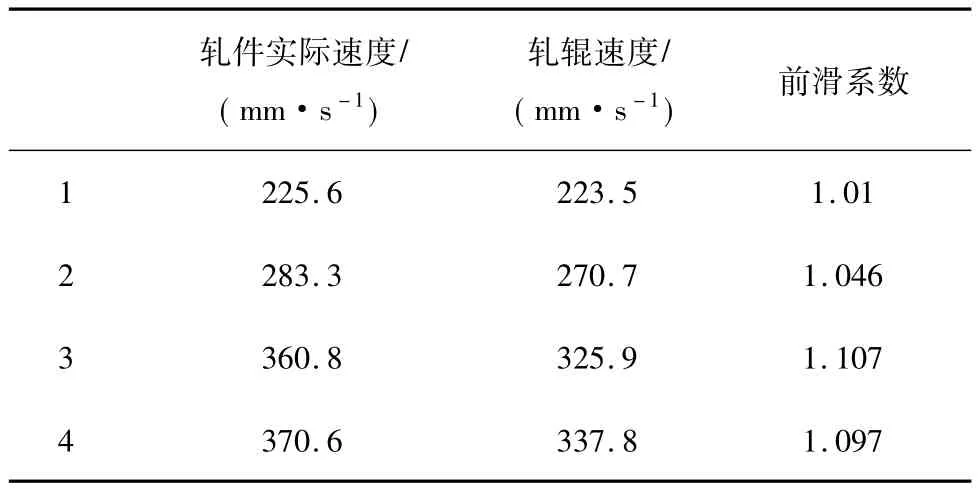
表1 前滑系数

图5 轧件实际轧制方向速度与轧辊轧制方向线速度
将图3所示横截面转化为autocad图形后,获得4道次填充系数(表3)。

表3 填充系数
3 结果分析
图6所示为有限元模拟过程轧件实际堆拉状态,轧件连轧过程前3机架之间呈波浪形弯曲状态,为堆钢状态,机架3、4之间轧件笔直,为拉钢状态。根据改进后的堆拉系数计算公式(2),机架1、2之间为堆钢轧制,堆拉系数为0.971,机架2、3之间为堆钢轧制,堆拉系数为0.879,机架3、4之间为拉钢轧制,堆拉系数为1.101,因此,与实际情况相符。利用传统堆拉系数计算公式(1),1、2机架与2、3机架堆钢系数分别为0.964、0.945,均为堆钢轧制,而3、4机架堆钢系数为0.976,为堆钢状态,与实际不符。显然,传统堆拉系数数学模型为考虑填充率影响,导致连轧过程堆拉关系错误。

图6 连轧过程轧件示意图
填充系数与堆拉系数关系总结如下:
(1)传统堆拉系数计算为堆钢轧制时,即ki<1,如果第i与第i+1机架填充系数比时,实际轧件一定为堆钢状态,但轧件堆拉强度小于传统计算值;相反时,轧件实际状态可能为堆钢或拉钢状态。
(2)传统堆拉系数计算为拉钢轧制时,即ki>1,如果第i与第i+1机架填充系数比时,轧件实际状态可能为堆钢或拉钢状态;相反1时,实际轧件一定为拉钢状态,但轧件堆拉强度大于传统计算值。
因此,传统堆拉系数公式,忽略了填充系数的影响,对于前后机架填充系数比率大的棒材轧制而言,可能导致结果错误,从而导致连轧过程张力轧制难以实现。然而,轧件填充系数不能准确确定,没有科学可靠的理论公式,借助于有限元,不失为一个好方法,为制定合理的轧制工艺方案提供了参考。
4 结语
在分析连轧堆拉关系的过程中,引入填充系数这一参数,从而获得了改进后的堆拉系数数学模型,并以梯形不锈钢筛条为例,借助于大型有限元软件进行连轧过程三维有限元模拟,验证了改进后的数学模型的科学性、精确性。
(2)改进后的堆拉系数数学模型,适用性广泛,为实际连轧过程堆拉关系的确定提供了科学、可靠的理论依据。
(3)考虑到目前填充系数参数确定困难,可以借助于有限元方法,实现填充系数的预估,从而为产品轧制工艺参数方案特别是堆拉关系的优化改进提供了参考。
[1]张小平,秦建平.轧制理论[M].北京:冶金工业出版社,2006.
[2]王廷溥.金属塑性加工学[M].北京:冶金工业出版社,1986.

