基于入射角的两项流体阻抗反演方法

李超，印兴耀，张广智，王保丽，刘倩

中国石油大学（华东）地球科学与技术学院，青岛 266580

1 引言

叠前地震反演已成为获取储层流体敏感参数的重要途径并得到了广泛应用.叠前地震反演方法大体可分为三类：基于波动方程的叠前反演、基于Zoeppritz方程或其近似的AVO／AVA反演和叠前弹性阻抗反演（Mallick，1995）.弹性阻抗反演方法简洁、方便、效率高，在抗噪能力和稳定性方面比其他两种方法具有优势（Cambois，2000），其实际应用效果也更好（Karimi et al.，2013；Westeng et al.，2014）.

弹性阻抗的概念最初由Connolly（1999）提出，由于其对非零炮检距数据的反演具有较高的稳定性，随后得到了广泛的认可.Whitcombe等（2002）提出了扩展的弹性阻抗的概念，扩大了弹性阻抗的定义域；Verwest等（2000）根据射线传播理论提出了射线阻抗的概念，将弹性阻抗理论扩展到射线域；倪逸（2003）结合相邻层速度和密度的不同变化规律，提出了基于范数动态可调的弹性阻抗计算方法；马劲风（2003）提出了适用于叠后资料的广义弹性阻抗；Wang等（2006）提出了基于Gray近似方程的弹性波阻抗反演方法，通过反演和参数提取可以直接得到拉梅常数；印兴耀等（2010）基于Russell提出的多孔流体饱和弹性介质的近似方程，提出了包含流体因子f的弹性波阻抗方程及反演方法；Morozov（2010）将反射波、透射波和转换波的弹性阻抗都表示为矩阵形式，无需近似从而提高了计算精度；Zhang等（2012）根据弹性阻抗和射线阻抗的概念提出了新的射线阻抗概念，不仅提高了反射系数的精度而且提高了解释能力；Zong等（2013）推导出包含泊松比和杨氏模量的弹性阻抗方程，建立了相应的直接反演算法.随着地质统计学反演理论的快速发展，一些学者提出利用地质统计学反演方法来反演弹性阻抗，取得了良好的效果（Ruiz et al.，2012；Azevedo et al.，2013；Francis，2013）.

目前，广泛使用的弹性阻抗方程大多是由Aki近似方程及其他基于Aki近似方程得到的AVO近似方程经过推导得到的.方程通常是由三项组成的，而且包含密度项.在缺乏大角度地震资料或者地震资料数据信噪比较低的情况下，大角度反演的结果品质较差（李爱山等，2009），提取参数的过程中，参数矩阵的稳定性较差，造成最终提取的弹性参数误差较大.另外，由于密度项的参数权值在角度有限情况下较小，反演的难度更加大.为此，本文基于入射角AVO近似方程，结合弹性参数间的岩石物理关系，在保证方程精度的前提下推导得到了包含Russell流体项的两项AVO近似方程，并进一步推导出两项流体弹性阻抗方程，建立了相应的概率化叠前反演方法.该方法由于未知项只有两项，对叠前资料的角度要求较小，可以在缺少大角度地震资料的情况下使用，并得到较为合理的反演结果.

2 基于入射角的流体弹性阻抗

2.1 包含流体项的两项近似方程

Aki近似方程是常用的AVO近似方程，在实际应用中为方便使用经常将入射角作为角度参数.由于Aki近似方程是基于入射角和透射角的平均角度进行推导得到的，所以在界面两侧物性变化较大或入射角较大的情况下，该近似方程的计算结果会产生较大的误差.张广智等（2012）提出基于入射角的两项AVO近似方程来解决误差问题，笔者将该理论依据应用于Aki三项AVO近似公式，可以得到如下的近似方程：

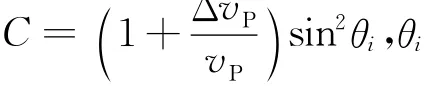
基于公式（1）推导得到的弹性阻抗反演方法能够得到比常规弹性阻抗反演方法更加精确的结果（Li et al.，2012），因此我们在此基础上进行推导.

根据Gardner公式（Gardner et al.，1974）以及纵横波阻抗的表达式可以得到：

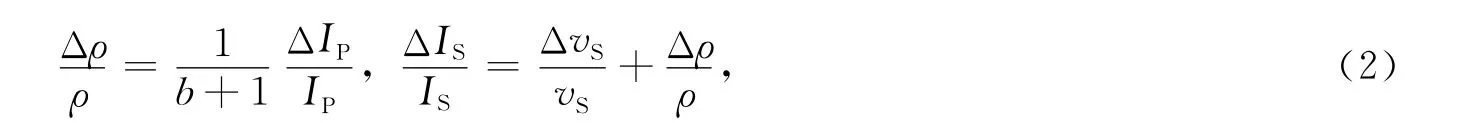
将公式（2）代入公式（1），可以得到：

Russell等（2003）对饱含流体多孔介质的AVO理论进行了研究，提出了流体项F（F＝fρ）.根据纵横波速度、密度与模量的关系可以得到：

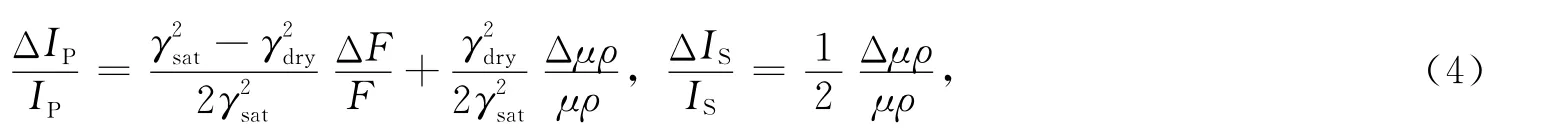
公式（4）代入公式（3）可得：

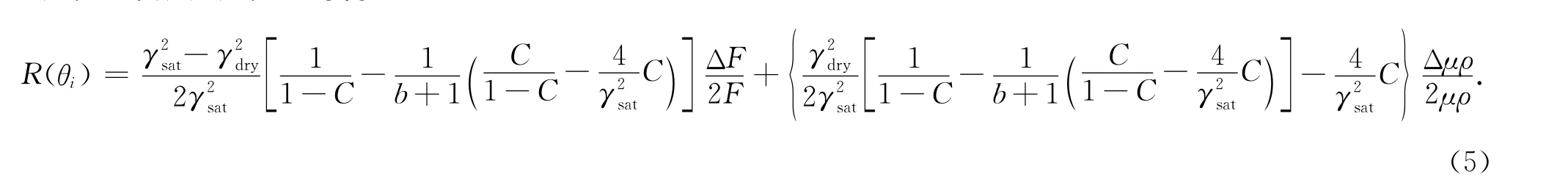
公式（5）即基于入射角的包含Russell流体项的两项AVO近似方程.

2.2 流体弹性阻抗方程

与普通弹性阻抗方程推导过程类似，反射系数可以表示为：

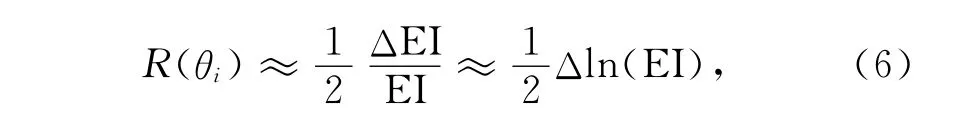
其中，EI是弹性阻抗.

由公式（6）可得：

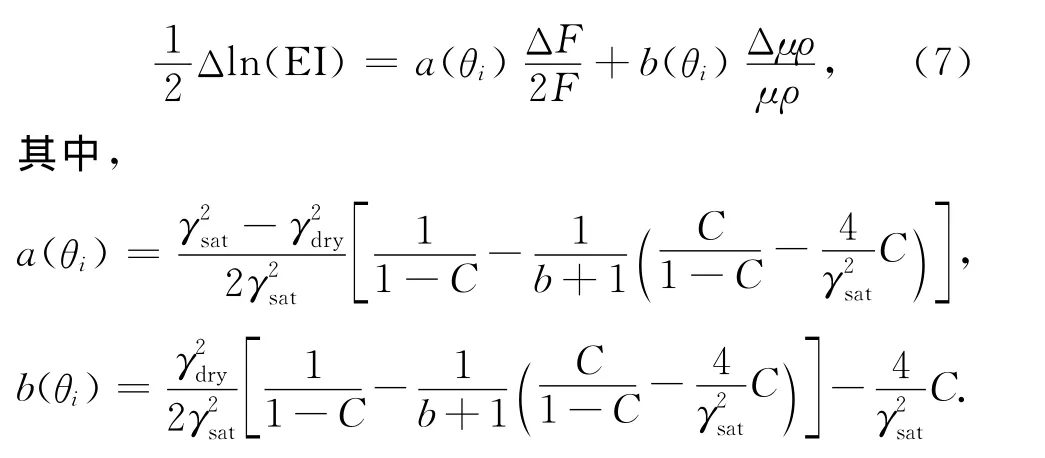
取积分并指数化，把积分常数设为0：

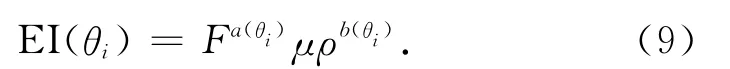
类似于常规的弹性阻抗公式，公式（9）也存在求取的弹性阻抗值随着角度的变化在量纲尺度上有很大变化的问题，这不利于进行不同角度的弹性阻抗值之间的对比以及与波阻抗值的对比.在综合分析波阻抗与弹性阻抗时，首先要将弹性阻抗变换到波阻抗的量纲尺度上，这给实际工作带来了不便.为了解决这个问题，消除入射角变化对量纲尺度的影响，要对推导出的弹性阻抗公式进行标准化处理（Whitcombe，2002）.引入了2个参考常数：F0、μρ0，并把弹性阻抗方程修改为

如果这些常数值被定义为F、μρ曲线的平均值，这样求得的弹性阻抗值就会在单位1附近变化，这一修改使得函数不再依赖尺度.为了使得弹性阻抗的尺度与波阻抗一致，利用θi＝0°时的弹性阻抗值进行加权处理，即

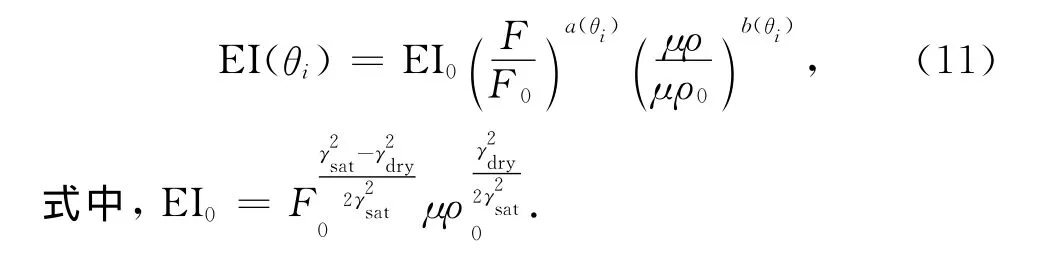
2.3 精度分析

为了验证新弹性阻抗方程的准确性，使用经典的Ostrander模型进行精确度定量分析，模型数据如表1所示.

表1 Ostrander的三层含气砂岩与页岩模型Table 1 Model for gas－bearing sand and shale designed by Ostrander

入射介质波阻抗小于透射介质波阻抗的界面称为正波阻抗界面，反之称为负波阻抗界面.上述模型中，上覆页岩和下伏含气砂岩的反射界面就是负波阻抗界面，而上覆砂岩和下伏页岩的反射界面为正波阻抗界面.以上述模型为基础分别用精确的Zoeppritz方程、公式（11）（记为 TEI）、Connolly弹性阻抗方程（记为CEI）、基于入射角的弹性阻抗方程（记为IEI）计算了界面处的反射系数，如图1a，1b所示.

从图1a中可以看出，在角度较小（小于15°）时，几种公式计算结果接近.随着角度逐渐增大，IEI计算结果与精确Zoeppritz方程的计算结果吻合度比较高，这符合IEI的性质；TEI作为IEI的两项近似也有较高的精确度，在角度增加到40°时与精确值的误差仍然非常小；而CEI在角度大于20°以后误差逐渐增大，精度已经不满足弹性阻抗反演的需求.在图1b中可以得到类似的结论，因此可以认为新的弹性阻抗方程的精度符合弹性阻抗反演的要求，而且高于常规弹性阻抗方程.

3 基于贝叶斯理论的弹性阻抗反演

基于入射角的弹性阻抗反演需要综合地质、测井和地震的资料，它以包含丰富地下信息的地震反射资料为主要资料，以地质和测井资料作为约束，来揭示地下储层的属性及其含流体特征.主要包括以下步骤：地震资料处理、测井资料处理、子波的提取与标定、弹性阻抗反演.为了更好地利用待反演参数的先验信息和提高反演结果的合理性，本文采用基于贝叶斯理论的弹性阻抗反演方法.

基于贝叶斯理论得到的反射系数r的后验概率密度函数可表示为：

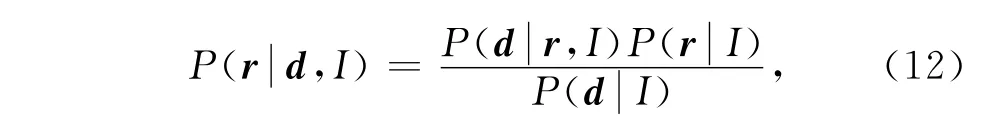
其中，向量d表示部分角度叠加数据向量；向量r表示待反演角度反射系数向量；I表示地质信息；）表示后验概率密度函数；表示描述观测数据d和反射系数r之间关系的似然函数；是先验概率密度函数；表示边缘分布，当只考虑后验分布的形状时，其数值可以取常数.

假设地震资料背景噪声服从高斯分布，地震数据和反射系数之间的关系可以用服从Gauss分布的似然函数来描述.假设先验信息服从Cauchy分布，将先验分布函数和似然函数代入贝叶斯公式可得：

将（13）式代入边缘化公式，取对数后得到最大化后验概率分布目标函数为

（14）式通过Cauchy先验分布加入稀疏约束提高了反演结果的稀疏性.但是由于地震资料是带限的，所以利用（14）式进行反演得到的结果也是带限的.而补偿低频信息可以改善反演剖面的横向连续性，提高反演结果的精度.为此本文通过加入平滑正则约束项和点约束项，对反演结果低频分量进行补偿.则目标函数进一步表示为：

其中，JSmooth（r）＝α‖C1r－η1‖2，JPoint（r）＝β‖C2rη2‖2.式中，α，β为加权系数，控制约束信息的相对使用量.可以看出平滑正则约束项和点约束项的数学表达式是相同的，但物理意义不同，主要体现在积分矩阵C的构建上.对于平滑正则约束项，C1和η1是由反射系数序列时间采样点的数目和低频模型或非常平滑单井模型计算得到；在点约束项中，C2和η2是由约束点的位置和对应位置处测井数据或井插值数据计算得到.

因此，式（15）即为最终的目标函数，对目标函数求梯度并令其等于0，得到如下反演方程：

从式（16）所示的反演方程可以看出，该方程有一定的弱非线性，因此采用迭代重加权最小二乘算法进行求解即可得到最终的结果.

从反演得到的弹性阻抗数据中提取流体因子等弹性参数是叠前地震反演的重要步骤，在此考虑直接提取Russell流体项F，一方面可避免间接计算带来的累计误差；另一方面两个角度的弹性阻抗建立的方程稳定性更高.

4 模型试算

为了验证基于入射角的流体弹性阻抗反演方法的可行性，本文选取 Marmousi2模型（Martin et al.，2006）的部分数据建立二维模型（图2a，2b），在时间0.9～1.0s、CDP300～500处有一含气储层，时间1.45～1.55s、CDP250～850处有一含油储层.从图2a中可以很清楚地看到气层和油层，说明Russell流体项对于区分油气层效果非常好，而在图2b中油气层都不清楚，说明μρ本身的指示能力较差.

图1 精确Zoeppritz方程（红色实线）、TEI（蓝色点线）、CEI（绿色点线）、IEI（粉色点线）计算的反射系数（a）负波阻抗界面反射系数对比；（b）正波阻抗界面反射系数对比.Fig.1 AVO curve computed with the exact Zoeppritz equation（red line），TEI（blue line），CEI（green line）and IEI（purple line）（a）Comparison of coefficients at positive interface；（b）Comparison of coefficients at negative interface.

图2 模型数据（a）Russell流体项；（b）μρ.Fig.2 The model（a）Russell fluid term；（b）μρ.

图3 纵波速度与密度做对数后的交会Fig.3 Crossplotting of the logarithm of P－velocity and density

利用图2数据进行正演得到1°到30°角度地震数据，得到中心角分别为5°、10°、15°的三个角度叠加道集.为了得到公式（11）中的常数b值，从模型中抽取几道作为伪井，对纵波速度和密度取对数进行交会，如图3所示.经过线性拟合可以得到二者的线性关系表达式，其中斜率参数0.26即为b的取值.利用本文方法对5°和10°数据进行叠前弹性阻抗反演，并提取弹性参数直接得到Russell流体项和μρ，如图4a，4b所示.分别对比图2a，2b和图4a，4b，可以看出通过本方法估算得到的Russell流体项和μρ与模型值基本一致，精确度较高.为了检验方法的抗噪性，在叠前道集数据中加入信噪比为4∶1的随机噪声，再进行如前的叠加和反演.估算得到的Russell流体项如图5a所示.对比图5a和图2a可以看出，虽然受到噪声的影响，但是估算得到的Russell流体项精确度依然非常高.

为了体现直接提取Russell流体项的优势，采取基于Connolly弹性阻抗方程的常规弹性阻抗反演方法，利用三个角度道集进行反演得到纵横波速度、密度后间接计算得到Russell流体项，如图5b所示.对比图5a和5b可以看出，由于经过了间接计算，反演过程中的误差得到了进一步的累积，因此图5b的结果受噪声影响更大，Russell流体项预测效果差于图5a的结果.为了更加直观地比较两种结果的差别，抽取CDP400的同时经过气层和油层的单道数据进行对比，如图6.从图中可以看出，直接提取的结果与模型精确值更加接近，间接方法得到的结果误差较大.通过以上比较可以看出，在缺少大角度地震资料的情况下，本文的反演方法依然可以得到准确的反演结果，而且由于系数矩阵条件数较小，稳定性得到了保证.

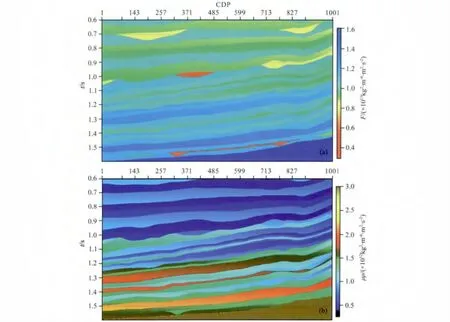
图4 无噪声情况反演结果（a）Russell流体项；（b）μρ.Fig.4 Inversion result without noise（a）Russell fluid term；（b）μρ.

图5 信噪比为4∶1时的反演结果（a）本文方法得到的Russell流体项；（b）间接方法得到的Russell流体项.Fig.5 Inversion result when S／N＝4∶1（a）Russell fluid term inverted by the new method；（b）Russell fluid term calculated by indirect method.

图6 信噪比为4：1时的反演结果抽取过CDP400的单道Fig.6 CDP 400of the inversion result when S／N＝4∶1

5 实际工区

实际资料来自中国东部某油田，由于目标储层埋藏较深，无法获取高质量的大角度地震数据，因此应用两项弹性阻抗公式进行叠前反演和储层预测.

进行叠前反演之前，需要对地震数据、测井数据进行预处理.地震数据预处理主要是保幅处理，测井数据的预处理主要是井数据的拼接和校正.

油砂岩，绿点表示含水砂岩，蓝点表示泥岩.从图中可以看出，Russell流体项能够很好地区分含油砂岩和含水砂岩，因此可以作为本工区的流体指示参数.

图7 Russell流体项和μρ的交会图Fig.7 Crossplotting of Russell fluid term andμρ

图8 不同角度的部分角度叠加道集（a）小角度叠加道集；（b）中角度叠加道集.Fig.8 Seismic profiles with different angle range（a）Seismic profile of small angle－stack；（b）Seismic profile of middle angle－stack.

经过叠前处理，将共反射点道集由偏移距域转换到角度域，并得到中心角为8°（3°～13°）和18°（13°～23°）的部分角度叠加道集数据，如图8a，8b所示.

图8a，8b中CDP405处有一口井，井上的柱状曲线是储层流体解释曲线，红色部分是含油砂岩，绿色部分是含水砂岩，蓝色部分是非储层.利用本文方法进行弹性阻抗反演，得到的Russell流体项和μρ如图9a，9b所示.从图9a中可以看到，井上所示2.63～2.66s处的油层对应较低的Russell流体项值，而2.39～2.41s处和2.48～2.51s处的水层也对应较低的异常值，但是明显高于含油层的值，储层流体得到了很好的识别.该结果与岩石物理交会分析结果以及实际钻井资料匹配较好.

上述工区取得较好的应用效果后，在另外一个工区进行实际应用.该工区目的层埋深与前述工区相比较浅，但是由于数据采集条件的限制无法得到高质量的大角度数据，因此使用相同方法进行弹性阻抗反演和储层流体识别.图10是最终得到的弹性参数剖面.与图9类似，Russell流体项剖面可以较好地指示含油储层，应用效果较好.

6 结论

图9 反演后提取的弹性参数（a）Russell流体项；（b）μρ.Fig.9 Elastic parameters extracted with inversion results（a）Russell fluid term；（b）μρ.

图10 另一工区反演得到的弹性参数（a）Russell流体项；（b）μρ.Fig.10 Elastic parameters extracted in another project（a）Russell fluid term；（b）μρ.

本文针对地震数据角度范围较小的情况，基于孔隙弹性介质理论和入射角AVO理论推导出了包含Russell流体项的两项弹性阻抗方程，并建立了基于贝叶斯框架的弹性阻抗反演方法，能够直接提取Russell流体项，不仅使解的稀疏性更高，而且避免了累积误差，提高了计算结果的精度.经过经典模型的试验和实际资料的应用，证明了基于入射角的两项流体阻抗反演方法有较高的准确性和较强的实用性.该方法由于未知项只有两项，对叠前资料的角度要求较小，可以在缺少大角度地震资料的情况下使用，并得到较为合理的反演结果.

Azevedo L，Nunes R，Correia P，et al.2013.Multidimensional scaling for the evaluation of a geostatistical seismic elastic inversion methodology.Geophysics，79（1）：M1－M10.

Cambois G.2000.AVO inversion and elastic impedance.71th Ann.Internat Mtg.，Soc.Expi.Geophys.，Expanded Abstracts，142－145.

Connolly P.1999.Elastic impedance.The Leading Edge，18（4）：438－452.

Francis A M.2013.Limitations of constraining reservoir model facies and properties using seismic impedance data.75th EAGE Conference ＆Exhibition，Expanded Abstracts.

Gardner G H F，Gardner L W，Gregory A R.1974.Formation velocity and density－the diagnostic basics for stratigraphic traps.Geophysics，39（6）：770－780.

Karimi S H，Karbalaali H，Shadizadeh S R，et al.2013.The application of elastic impedance inversion and pre－stack attribute analysis for prospect identification—a case study.75th EAGE Conference ＆Exhibition，Expanded Abstracts.

Li A S，Yin X Y，Lu N，et al.2009.Application of elastic impedance inversion with two angle stack gathers to predict gasbearing reservoir of mid－deep layer.Oil Geophysical Prospecting（in Chinese），44（1）：87－92.

Li C，Yin X Y，Zhang G Z.2012.Elastic impedance equation based on the incident－angle approximation and inversion.74th EAGE Conference ＆Exhibition，Expanded Abstracts.

Ma J F.2003.Forward modeling and inversion method of generalized elastic impedance in seismic exploration.Chinese J.Geophys.（in Chinese），46（1）：118－124.

Mallick S.1995.Model－based inversion of amplitude－variationswith－offset data using agenetic algorithm.Geophysics，60（4）：939－954.

Martin G S，Wiley R，Marfurt K J.2006.Marmousi2：An elastic upgrade for Marmousi.The Leading Edge，25（2）：156－166.

Morozov I B.2010.Exact elastic P／SV impedance.Geophysics，75（2）：C7－C13.

Ni Y.2003.A new method for calculation of elastic wave impedance.Oil Geophysical Prospecting （in Chinese），38（2）：147－150，155.

Ruiz R，Pérez Y，Álvarez P.2012.Seismic impedance inversion and statistical rock physics for lithofacies discrimination：Case study for a siliciclastic and a carbonate reservoir.83th Ann.Internat Mtg.，Soc.Expi.Geophys.，Expanded Abstracts，1－5.

Russell B H，Hedlin K，Hilterman F J，et al.2003.Fluid－property discrimination with AVO： A Biot－Gassmann perspective.Geophysics，68（1）：29－39.

VerWest B，Masters R，Sena A.2000.Elastic impedance inversion.71th Ann.Internat Mtg.，Soc.Expi.Geophys.，Expanded Abstracts，1580－1582.

Wang B L，Yin X Y，Zhang F C.2006.Laméparameters inversion based on elastic impedance and its application.Applied Geophysics，3（3）：174－178.

Westeng K，Hope T A，Rasmussen A E.2014.Extended elastic impedance — a time－efficient workflow from prestack seismic data，through rock physics，to reservoir properties.International Petroleum Technology Conference.

Whitcombe D N.2002.Elastic impedance normalization.Geophysics，67（1）：60－62.

Whitcombe D N，Connolly P A，Reagan R L，et al.2002.Extended elastic impedance for fluid and lithology prediction.Geophysics，67（1）：63－67.

Yin X Y，Zhang S X，Zhang F C，et al.2010.Utilizing Russell approximation based elastic wave impedance inversion to conduct reservoir description and fluid identification. Oil GeophysicalProspecting （in Chinese），45（3）：373－380.

Zhang F，Wang Y H，Li X Y.2012.Viabilities of seismic ray impedance and elastic impedance for hydrocarbon－sand discrimination.Geophysics，77（4）：M39－M52.

Zhang G Z，Zheng J J， Wang Y M，et al.2012. AVO approximation and attribute extraction based on the incident angle.Oil Geophysical Prospecting （in Chinese），47（4）：578－583.

Zong Z Y， Yin X Y， Wu G C.2013.Elastic impedance parameterization and inversion with Young′s modulus and Poisson′s ratio.Geophysics，78（6）：N35－N42.

附中文参考文献

李爱山，印兴耀，陆娜等.2009.两个角度弹性阻抗反演在中深层含气储层预测中的应用.石油地球物理勘探，44（1）：87－92.

马劲风.2003.地震勘探中广义弹性阻抗的正反演.地球物理学报，46（1）：118－124.

倪逸.2003.弹性波阻抗计算的一种新方法.石油地球物理勘探，38（2）：147－150，155.

印兴耀，张世鑫，张繁昌等.2010.利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别.石油地球物理勘探，45（3）：373－380.

张广智，郑静静，王玉梅等.2012.基于入射角的AVO近似及属性提取.石油地球物理勘探，47（4）：578－583.