大跨度连续刚构墩梁固结分析

张树清 郑国华

(安徽省交通规划设计研究院有限公司桥梁分院，安徽 合肥 230088)

大跨度连续刚构墩梁固结分析

张树清 郑国华

(安徽省交通规划设计研究院有限公司桥梁分院，安徽 合肥 230088)

采用ANSYS 建立连续刚构墩梁固结有限元模型，对其结构进行安装后的多种工况静力分析，得到其应力情况，结果表明该安装方案在静结构强度方面表现良好，设计合理，墩梁固结区应力均满足设计规范要求。

连续刚构，墩梁固结，有限元，静力分析

某桥主桥跨径布置为(97+176+97)m，全长370 m，为连续刚构桥方案，结构体系采用墩梁固结的形式。主梁采用单箱单室变高度箱梁，主墩采用双薄壁墩，下部采用承台及群桩基础。

主梁采用预应力混凝土变高度箱梁，主梁全宽32.0 m。箱梁支点梁高10.0 m，跨中梁高4.5 m，行车道部分顶板厚度为0.28 m，翼缘板边缘厚度0.20 m。底板厚度由跨中0.32 m变化到支点处1.20 m。腹板采用分段等宽，由跨中到支点分两次变化，厚度分别为0.50 m，0.65 m，0.80 m。主梁端支点及中支点处均设置横隔梁，端横隔梁厚度2.00 m，中横隔梁厚度2.00 m，中横隔梁单个支点上设置两道，分别与两道薄壁墩固结。主墩采用双薄壁墩形式，主墩横桥向标准宽度9.95 m。顺桥向为等宽，宽度1.6 m。两个薄壁墩间距为4.0 m。主墩基础采用承台及群桩基础，承台采用矩形承台，承台分上下两层，总高5.0 m，下层高3.0 m，横桥向宽14.0 m，顺桥向宽19.0 m，上层高2.0 m，横桥向宽10.95 m，顺桥向宽11.0 m，见图1。

1 计算模型

1.1 有限元模型

由于连续刚构桥的墩梁固结区的构造和应力分布都较为复杂，为考察墩梁固结区域在不利施工工况下受力状况，直观的看出该区域应力分布情况，采用大型通用有限元软件ANSYS建立墩梁固结区域有限元模型，如图2所示。根据圣维南原理，墩梁固结区的应力分布只与其附近区域的受力状态有关，有限元模型截取双薄壁墩墩柱和承台，箱梁顺桥向截取52 m模拟研究。

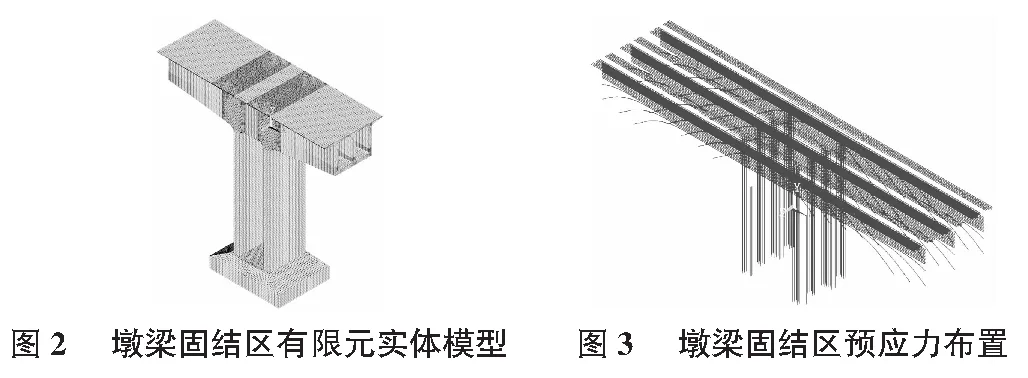
墩梁固结区域承台、桥墩、箱梁混凝土部分采用实体单元Solid65模拟，划分单元网格时尽量采用正六面体单元，以保证计算结果的准确性。模型计算中考虑预应力钢束作用，按预应力实际布置情况模拟，如图3所示，预应力钢束用杆单元Link8模拟。预应力钢束预加应力是通过对杆单元施加降温实现，预应力钢束与混凝土之间的连接关系通过自由度耦合来模拟，计算中不考虑普通钢筋的作用。

1.2 荷载工况

桥梁施工过程复杂，施工工况很多，针对每个施工工况都进行墩梁固结局部分析，耗时耗力。在局部分析中结合整体计算的工况结果，选取对结构最不利几个工况进行局部分析。综合考虑共选取四种荷载工况:工况一，最大双悬臂，即是挂篮悬浇施工边跨、中跨均未合龙状态；工况二，最大单悬臂，即是挂篮悬浇施工边跨合龙、中跨合龙前状态；工况三，正常使用极限状态组合Ⅲ(弯矩最大)；工况四，承载能力极限状态(弯矩最大)。

各工况下梁端荷载表见表1。

表1 各工况下梁端荷载

1.3 边界条件

局部分析计算中有限元模型的边界条件可分为位移边界条件和力的边界条件，分析中在考虑边界条件与实际结构近似的同时，对无法准确模拟的边界条件按偏安全处理。在局部分析模型的两端施加整体计算得到的力的边界条件，在双薄壁墩承台底部施加约束所有自由度位移边界条件[2]。

2 局部分析结果

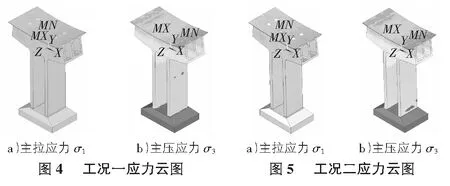
各工况计算应力分布情况如图4～图7所示。

从图4～图7可以看出：

1)边、中跨均未合龙，结构处于最大双悬臂时，墩梁固结区域箱梁顶板压应力-11.2 MPa～-20.9 MPa，腹板压应力-8.02 MPa～-14.5 MPa，底板应力-4.8 MPa～-8.02 MPa；

2)边跨合龙，中跨尚未合龙，结构处于最大单悬臂时，墩梁固结处箱梁顶板的压应力为-11.5 MPa～-21.4 MPa，腹板压应力-8.19 MPa～-18.1 MPa，底板应力-4.89 MPa～-8.19 MPa；

3)正常使用极限状态荷载组合Ⅲ最大弯矩工况下，顶板压应力-11.1 MPa～-20.6 MPa，腹板压应力-8.01 MPa～-17.6 MPa，底板应力-4.78 MPa～-8.01 MPa；

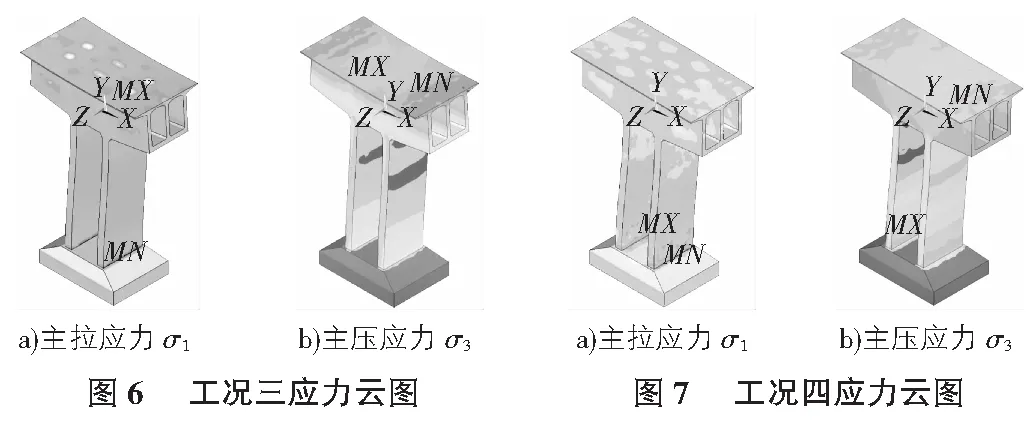
4)承载能力极限状态最大弯矩工况下，顶板压应力-3.5 MPa～-5.86 MPa，腹板压应力-5.86 MPa～-10.6 MPa，底板应力-8.21 MPa～-12.9 MPa；

5)单悬臂状态箱梁顶板应力边跨侧稍微大于中跨侧，箱梁底板应力中跨侧稍微大于边跨侧；正常使用极限状态荷载组合Ⅲ箱梁顶板、底板压应力较最大双悬臂、最大单悬臂状态应力减小。除承载能力极限状态外，结构在各工况下主应力数值相差不大。各工况作用下墩梁固结区域截面均处于受压状态，受力满足设计规范要求。

3 结语

采用ANSYS 对墩梁固结段建立了比较精细的有限元模型，对其进行静力强度分析。结果显示该方案在静结构强度方面表现良好，设计合理。墩梁固结区应力满足要求，预应力钢束布置合理。建议在满足施工的条件下，在拉应力比较大的区域，适当增加钢筋密度；在压应力比较大的区域，适当考虑构件局部增强，考虑局部承压设计。

[1] JTJ 023-85，公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

[2] 高 伟.大跨度连续刚构桥墩梁固结区受力分析[J].大连大学学报，2009(4)：23-25.

[3] 王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社，2007.

[4] 周敬库.铁路连续刚构桥墩梁固结处的局部应力分析研究[J].铁道建筑，2008(23)：57.

[5] 夏 龙.高墩大跨T型刚构桥墩梁固结处试验研究[D].长沙：中南大学，2008.

Analysis of joint between piers and girder of long-span continuous rigid frame bridge

ZHANG Shu-qing ZHENG Guo-hua

(BridgeBranchCourtsofAnhuiTransportConsulting&DesignInstituteCo.,Ltd,Hefei230088,China)

The FEM local analysis of joint between piers and girder of the bridge were performed by using ANSYS program. Stress distributions of the joint in construction stages and working stages were obtained by static calculation of a variety of conditions. Proves by the result that the scheme has better performances in the strength of the static structure and has reasonable design, and the stress at pier beam consolidation area can meet the requirements for the design regulation.

continuous rigid-frame, joint between piers and girders, FEM, static analysis

1009-6825(2014)11-0180-02

2014-02-07

张树清(1983- )，男，硕士，工程师； 郑国华(1975- )，男，高级工程师

U443.22

A