钢筋混凝土中的粘结应力与滑移的关系

刘 晓 军

(太原市政府投资项目评审中心，山西 太原 030014)

钢筋混凝土中的粘结应力与滑移的关系

刘 晓 军

(太原市政府投资项目评审中心，山西 太原 030014)

基于常规的粘结滑移理论，并结合钢筋与混凝土截面变形特性提出了一种分析模型，建立了一个无量纲的函数方程，同时将结果与实验进行了对比，得出其一致性较好的结论。

钢筋混凝土，应力，粘结

1 概述

钢筋与混凝土的粘结对混凝土结构有重要的影响。由于粘结影响着钢筋的锚固和搭接强度，因此它是混凝土结构承载力的关键因素之一，同时也直接影响着构件的变形能力和超静定结构的应力重分布能力[1-3]。因此可以说钢筋与混凝土的粘结是混凝土结构最基本的问题。而目前主要的缺失是没有一种通用的方法来确定粘结强度。这就使得不同的实验和研究结果比较起来较为困难。大家通常都是采用直接拔出实验进行研究。但是大多数研究并没有把研究重点放在混凝土中的嵌固长度和应力状态，同时也未注意到实验与实际工程中的嵌固长度与应力状态差别是很大的。

通常，钢筋混凝土中的粘结行为是粘结应力与滑移关系。研究者已经提出了很多粘结应力滑移关系并将之公式化，运用到有限元方法和裂纹分析当中去。但结果却千差万别，就是由于粘结应力的复杂性以及拔出实验无法真正模拟实际的工作状态。因此，粘结应力关系应当考虑构件的实际应力工作状态，如受弯构件通常在裂纹面处有较长的嵌固长度和轴向拉伸应力。正是由于影响因素很多，因此有很多研究者提出了在各自实验条件下的描述粘结行为的公式，它们各有特色，如Ikkit[4,5]等提出了一种轴向拉伸实验下的粘结公式：

(1)

其中，ksf为混凝土应力状态系数，压缩取1.0，拉伸取0.7；kd为混凝土中浇筑混凝土时钢筋走向系数，垂直浇筑取1.0，水平浇筑取0.9；f′为混凝土强度；s为滑动长度；ds见图1。这一公式对于拉伸下的应力状态给出了很好的描述，然而这一公式不能给出滑移下的最大粘结力，而最大粘结应力是确定锚固长度，裂纹宽度和搭接长度的关键因素。本文提出了一种相对钢筋肋面积指数方程的分析方法来评估钢筋与混凝土的粘结行为。

2 粘结机制及公式的提出

因为钢筋混凝土是一种复合材料，因此载荷作用下钢筋与混凝土会发生滑动，因此粘结行为是滑移的函数。当外力一点点的加到混凝土构件上，界面应力就会在钢筋与混凝土之间产生，在某一载荷值下界面之间传递应力的能力就会减弱。这种不能恢复的损伤会在钢筋混凝土中传播和扩散，这样界面传递应力的能力会恶化，两种材料就会发生滑移。

如图2所示，界面间的应力传递机制通常是由钢筋拔出实验得到的，其中包含握裹力，摩擦力和剪切粘结力。而对于变形钢筋来说，主要的抗力来自于机械咬合力。事实上，对于带肋钢筋来说，其肋的几何形状控制着粘结行为和粘结强度。图1中所示的钢筋直径，肋高及肋间距均对钢筋与混凝土之间的粘结力产生重要的影响。Rehm[7]的研究显示，肋的相对面积是钢筋与混凝土之间粘结力的一个重要参数，同时肋面的倾斜角也是重要影响因素。实验显示，当肋面倾斜角为30°时，最高的粘结力对应的相对面积在0.05～0.15之间。

这里相对面积表达式为：

(2)

其中，AR为肋单侧的面积，其他符号意义如图1所示。另外其粘结力与钢筋的埋置长度有关，对于埋置长度较短的钢筋混凝土来讲，其粘结应力随着相对肋的面积的增加而显著增加，而对于埋置长度较长的构件而言其增长是缓慢的，而且其最大的粘结应力要远小于短埋置长度。通常采用拔出实验和单轴拉伸实验来获得钢筋与混凝土之间的粘结应力与滑移的关系，而拔出实验又分为单边拔出和双边拔出。但拔出实验的主要缺点是不能够反映真实的构件受力情况。这是由于试件的反向夹持力会在混凝土中产生压缩应力，而实际情况则是在钢筋与混凝土作用界面附近均处于拉伸应力状态。而单轴拉伸则不同，如图3b)所示，其中混凝土基本处于拉伸的应力状态，更接近于弯曲构件拉伸面的应力分布。因此单轴拉伸较拔出实验更符合构件的工作状态。基于单轴拉伸实验的应力分布情况，本文提出了一种描述粘结应力的公式，据Shima[6]的研究成果，粘结强度与混凝土的抗压强度成正比，因此我们采用其无量纲表达式在公式中表述其影响，同时考虑了钢筋直径的影响，再结合Ikki[4,5]等人提出的公式和考虑肋的相对面积的影响提出了以下公式作为描述钢筋混凝土粘结应力的表达式：

(3)

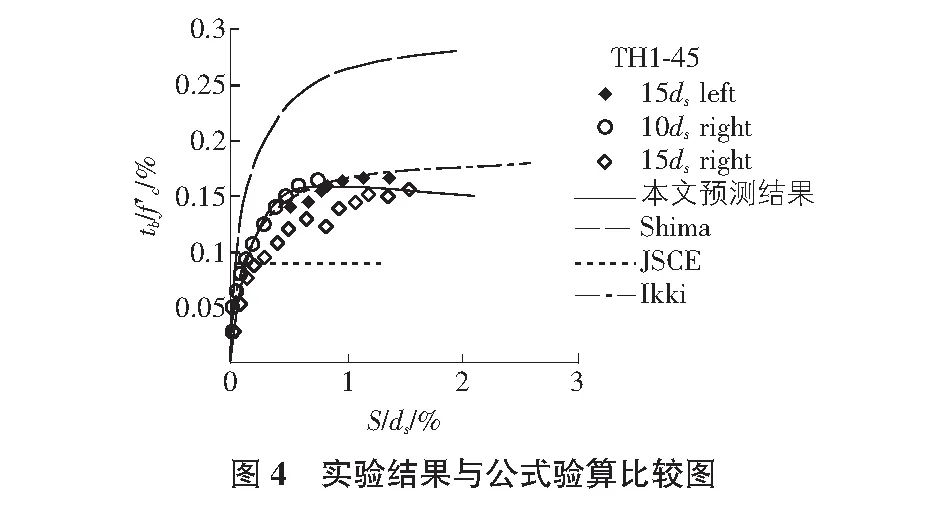
k为反应握裹力的系数，它依据浇筑情况以及有没有箍筋分别给出不同的表达式。fR为肋的相对面积系数。图4给出了实验及式(3)与其他公式预测的比较，由图4可以看出，式(3)与Ikki[4,5]的公式对实验结果的预测均符合的更好。

3 结语

本文提出了一种单轴拉伸实验下评估粘结滑移关系的分析公式，考虑了钢筋肋的相对面积对粘结应力的影响。并与实验结果及其他公式进行了比较，结果显示本公式可以很好的预测粘结应力。然而由于影响因素很多，同时一些因素不能定量的准确表述，因此对于粘结应力的预测仍需要进行很多实验及细致的分析，以便得到一个通用且宜用的公式。

[1] FIP，“Bond of reinforcement in concrete: state-of-art report,”Fib Bulletin No.10，CEB-FIP，Lausanne，Switzerland，2000.

[2] CEB-FIP，Structural Concrete—Textbook on Behaviour，Designand.Performance，Updated Knowledge of the CEB-FIP Model Code 1990，vol.1，Sprint-Druck，Stuttgart，Germany，1999.

[3] J.Dai，T.Ueda,Y.Sato.“Unified analytical approaches for determining shear bond characteristics of FRP-concrete.

[4] N.Ikki，O.Kiyomiya.Effect of axial concrete stress onbond strength of deformed bar[J].Proceedings of Japan Concrete Institute，1996，21(3)：373-378.

[5] N.Ikki，O.Kiyomiya，M.Yamada.Experimental study on the effects of numerous factors on bond-slip relationship[J].Journal of Materials，Concrete Structures and Pavements，1996，33(550)：73-83.

[6] H.Shima.Bond models micro and macro models for bond in reinforced concrete，Ph.D.thesis，Tokyo University，Tokyo，Japan，1987.

[7] G.Rehm.“The fundamental law of bond”,in Proceedings of the Symposium on Bond and Crack Formation in Reinforced Concrete，RILEM，Stockholm，Sweden，1957：491-498.

Relationship of bonding stress and slippage in steel reinforced concrete

LIU Xiao-jun

(TaiyuanMunicipalInvestmentProjectEvaluationCenter，Taiyuan030014,China)

Based on general bonding slippage theories, combining with steel reinforced section deformation characteristics, the paper puts forward a kind of analysis model, establishes a dimensionless function, and compares it with experiment result, and finds out its better consistency.

steel reinforced concrete, stress, bond

1009-6825(2014)11-0065-03

2014-01-20

刘晓军(1972- )，男，工程师

TU375

A