换土垫层厚度的简化计算法研究

陈 鲲 何 勇

(中国建筑第五工程局有限公司，湖南 长沙 410000)

换土垫层厚度的简化计算法研究

陈 鲲 何 勇

(中国建筑第五工程局有限公司，湖南 长沙 410000)

根据换土垫层法的基本理论，从安全和实用的角度出发，对换算厚度计算公式进行了简化,得出了关于垫层厚度的一元二次方程，通过对某工程案例的计算分析，指出该简化计算公式可方便地直接求解垫层厚度，计算过程简便，同时能很好的满足工程要求。

地基处理，换土垫层法,厚度，简化算法

0 引言

对于土木工程中的建筑结构，当持力层地质条件不好，承载能力不能满足设计要求时，可以采用地基处理的方法进行处理。换土垫层法就是其中常用的一种方法，其原理为挖去地基土里某一范围不满足要求的土层，随后在这些范围内填入强度和压缩性都满足条件的材料，比如砂、碎石以及一些高强和低压缩性的材料，再将这类材料进行压实，作为新的地基土的持力层。根据以往的工程经验，利用此方法进行地基的加固能够很好的满足土体受力要求。尤其是对一般的房屋结构，路堤等的换土垫层处理更为方便。能够根据现场情况方便的取材和缩短施工工期，从而降低工程造价。因此越来越多的工程在地基加固时选择了换土垫层法。换土垫层法根据材料不同一般分为砂垫层、灰土垫层、素土垫层等[1]。

垫层土的作用主要表现在以下两个方面:1)提高地基的承载力。因为土层受力过大发生剪切破坏会导致地基破坏，并且由于应力的增大，破坏会逐渐向深处发展。所以，换用抗剪强度大的材料，能明显抵抗地基发生的剪应力，防止发生剪切破坏。2)减小上部结构的沉降变形。在沉降中，浅层地基的沉降百分比很大，对于条形基础而言，此比例为50%左右。而且由于地基的侧向变形也会引起沉降，因此如果采用强度和压缩性都满足要求的材料进行换填,就能够大幅度减小地基的沉降量，同时将地基应力进行扩散，也起到了减小地基沉降量的作用。3)加快地基的排水固结。因为不透水基础将会与软弱地基层直接接触作用，在上部荷载作用下，软弱土层里的水会被排出，导致软弱地基层土体固结困难，以至于出现的孔隙水压力很大。甚至导致由于土体强度较低发生塑性破坏。垫层中的土体既可以充当基底下排水面，消散孔隙水压力,使土体不会发生塑性破坏，又能够提高强度，加快固结速度[2]。

换土垫层计算分析中，需要首先计算得出垫层的宽度和厚度。其中垫层的宽度是根据压力扩散角理论在已知垫层厚度的基础上计算得出的。故垫层的计算设计中，垫层厚度的确定是至关重要的一步。规范中对于厚度的计算方法规定如下：首先计算确定出土的自重应力σcz与附加应力σz之和σ，再由σ≤fz(软弱土地基承载力)，试算得到合适的取值。但在计算过程中，σcz,σz和fz会随垫层厚度发生变化。垫层厚度增大，fz,σcz将增大，σz将减小。故在实际计算中大多先假定垫层厚度为已知值Z0，反复试算，如果试算的结果不满足要求,则需改变厚度重新计算,直到得出满意的结果为止[3]。这种计算方法理论上可行，但是在实际计算过程中,存在明显的缺陷,需要反复迭代进行试算，非常繁琐。因此本文基于现行的计算方法,得到了换土垫层厚度计算的简化方法,计算量小,并且能够满足实际工程需要，避免了传统计算方法需反复试算的缺陷。

1 换土垫层基本理论

软弱下卧层经过修正后的地基承载力设计值为fz，下卧层附加压力设计值为σz，下卧层自重应力标准值为σcz，三者满足如下关系式[4]:

σz+σcz≤fz

(1)

(2)

σcz=(d+Z)γ0

(3)

fz=fk+ηbγ(b0-3)+ηdγ0(d+Z-0.5)

(4)

其中，b为矩形基础的宽度，m;p为矩形基础底面压力设计值，kPa；σc为土的自重应力,kPa,σc=γ1d；γ1为土体的平均重度,kN/m3；d为基础的深度,m;θ为底面压力扩散角;fk为不良土体的承载力标准值,kPa；ηd为地基承载力的深度修正系数;γ为软弱土体的重度,kN/m3;b0为垫层宽度,m；ηb为地基承载力宽度的修正系数;Z为垫层的厚度,m；γ0为底面以上土体的平均重度,kN/m3。

将式(2)～式(4)代入式(1)，可得：

(d+Z)γ0≤fk+ηbγ(b0-3)+ηdγ0(d+Z-0.5)

(5)

工程中较常见的软弱地基土的承载力标准值为50 kPa≤fk≤90 kPa。根据规范，可查ηb=0，ηd=1.1；取垫层底面以上土的平均重度γ0=18 kN/m3，将上述数据代入式(5)，可得:

fk+1.1×18×(d+Z-0.5)-18×(d+Z)

(6)

式(6)是关于垫层厚度Z的一元三次方程，需要进行迭代求解，因此本文根据安全实用的原则，将式(6)进行简化，由式(6)可得到：

fk+1.1×18×(d+Z-0.5)-1.1×18(d+Z)

(7)

化简可得：

(8)

由式(8)求垫层厚度Z的最小值，可得：

(9)

则式(9)即为换土垫层厚度的简化计算公式，为关于Z的一元二次方程，求解便可得到垫层厚度Z。

2 工程实例计算

拟建保利滨江B7地块-E-2-12号位于长沙市银盆岭大桥西端南侧，北侧为银盆岭路，东侧为拟建的长纺路，南侧为拟建桐梓坡路东路，交通方便，地理位置优越，其原始地貌单元属于湘江Ⅲ级阶地。规划总用地面积约41 459 m2，规划总建筑面积约258 182 m2，设置1层～3层地下室，设计地坪±0.00 m约为50.70 m～53.50 m(1985国家高程)。

根据钻探揭露，场地内埋藏的地层主要由填土层、粉质粘土层、圆砾、卵石、残积粉质粘土层、全风化板岩、强风化板岩、中风化板岩、淤泥质土组成。

建筑结构的基础采用矩形基础，基础的立面和平面布置图如图1和图2所示。

上部结构轴心荷载(±0.000)F=211.085 kN,地基土承载力标准值fk=50 kPa。计算中采用素土垫层进行换填,其压力扩散角为θ=22°,p=120 kPa，γ1=18 kN/m3,γ0=18 kN/m3,γG=20 kN/m3,基础埋深为d=0.8 m，求此工程中换土垫层的厚度Z。

首先需要确定矩形基础的参数。根据公式，可求得矩形基础的面积S：

由此，取矩形基础宽度b=1.2 m，长度l=1.6 m。

其次求矩形基础垫层的换土垫层厚度Z。

由式(9)可得：

4tan222°Z2+2×(1.2+1.6)tan22°Z+

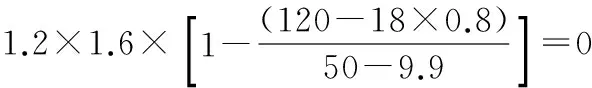
求解可得Z=1.43 m。

最后验算换填后的承载力能否满足要求。

fz=fk+ηdγ0(d+Z-0.5)=

50+1.1×18×(0.8+1.43-0.5)=84.254 kPa。

垫层土体底面处压力为:

(0.8+1.43)×18=79.61 kPa。

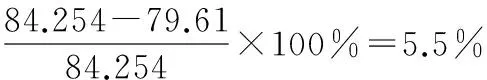
且84.254>79.61,由此得出的计算结果略偏安全，计算过程简便，能很好地满足工程需要。

3 结语

本文根据换土垫层法基本理论，将换土垫层法厚度的计算公式进行简化，得出偏于安全，适合求解的换土垫层法厚度的计算公式。此公式用于计算换土垫层厚度时，计算量小,结果精确,误差小,能够较好的满足实际工程要求。

[1] 黄生根,张希浩.地基处理与基坑支护工程[M].北京:中国地质大学出版社,1999.

[2] 王恩远,吴 迈.工程实用地基处理手册[M].北京:中国建材工业出版社,2005.

[3] 阎明礼.地基处理技术[M].北京:中国环境科学院出版社,1996.

[4] 黄运飞.深基坑工程实用技术[M].北京:兵器工业出版社,1996.

[5] 王 赫.建筑工程质量事故分析与防治[M].南京:江苏科学技术出版社,1990.

[6] 赵理杰.浅谈砂垫层法加固软土地基[J].石家庄铁道学院学报,1994,7(1):99-101.

[7] 刘顺义,范晓英.用换土垫层法处理软弱地基[J].沈阳建筑工程学院学报,1998,14(1):83-87.

[8] 雷 强.换土垫层法在某工程中的应用实例[J].福建建筑,2001(2):53-54.

[9] 姚 鹏,陈湘桂.砂石垫层法在软土地基中的应用—例析[J].安徽建筑,2003(1):77-78.

[10] 王文凯.垫层法在处理桥梁软弱地基的应用[J].辽宁交通科技,2004(2):37-39.

Simplified calculation method of cushion thickness in soil research

CHEN Kun HE Yong

(ChinaConstructionFifthEngineeringDividionCo.，Ltd,Changsha410000，China)

According to the basic theory of soil replacement cushion method, from the safe and practical point of view, this paper simplified the equivalent thickness calculation formula, gained the quadratic equation of cushion thickness, through the calculation and analysis of engineering cases, pointed out that the simplification formula could be easily directly solution of cushion thickness, the calculation process was simple, at the same time, could be very good to meet the engineering requirements.

foundation treatment, soil replacement cushion method, thickness, simplification algorithm

1009-6825(2014)35-0088-02

2014-09-22

陈 鲲(1986- )，男，工程师； 何 勇(1975- )，男，高级工程师

TU472.2

A