农产品价格波动的非对称性研究*

李正辉，徐亚丽

(湖南大学 金融与统计学院, 湖南 长沙 410082 )

农产品价格波动的非对称性研究*

李正辉，徐亚丽

(湖南大学 金融与统计学院, 湖南 长沙 410082 )

采用B-P滤波对1999-2012年我国农产品价格指数进行处理，观测到我国农产品价格呈现出4个波动性周期，并且表现出明显的不可重复性和非对称性；再利用描述性统计分析与非对称GARCH族实证模型相结合的方法检验我国农产品价格波动的非对称性；实证结果表明我国农产品价格波动的非对称性具有稳健性特征，并且EGARCH模型描述我国农产品价格波动的非对称性更为有效。最后绘制EGARCH模型的市场信息冲击曲线，进一步验证结论。

农产品；价格波动；非对称性

一 文献综述

农产品价格稳定与国民经济平稳运行有密切关联,也一直是世界各国农业宏观管理的焦点问题。如近两年连续出现的猪肉价格剧烈波动，2009年的广西香蕉每斤不足一毛钱，农民忍痛拿来喂牛，与此同时山东大蒜价格创历史新高，2010年海南辣椒价格一度下跌出现滞销的惨状，等等。农产品价格的反常态波动正是我国农产品市场监管欠缺的体现，也提升了对我国农产品价格波动研究的迫切性。

关于农产品价格波动的解释研究，其主要依据是供给理论。最著名的是由Schultz，Tinbergen提出，经Kaldor和Ezekiel改进的蛛网模型，模型中的具体参数用计量经济学模型可进行估计。随着研究的进一步深入，更多的学者通过各种数据对农产品价格波动的影响因素及传递路径进行理论探讨和实证分析，来研究农产品价格波动的成因及传导机制[1]。

Benavides[2]根据历史经验数据，采用时间序列模型对玉米和小麦价格做出分析，得出汇率、库存是影响玉米和小麦价格波动主要因素的结论，并在此基础上进一步做出了预测。Mitra[3]采用非线性Cobweb模型进行研究，其结果肯定了库存对粮食价格波动的重要影响。

顾国达、方晨靓[4]运用向量自回归(VAR)模型对价格在农产品各环节的传导进行模拟，进而对农产品价格波动的传导机制及其非对称特征进行分析，得出农产品价格传导机制具有非对称性的结论。Meyer[5]在对非对称价格传递的正负效应研究基础之上，对价格非对称传导模型进行进一步的完善；胡华平、李崇光[6]对我国农产品市场垂直价格传递和纵向市场联结的关系进行探究，尝试了非对称纵向价格传递的误差修正模型(APT-ECM)并通过实证分析得出基本结论：纵向市场联结的松散程度和非对称垂直价格传递特征的微弱性呈现正相关关系。

此外，徐高雪等[7]基于时间序列模型，通过H-P滤波对农产品价格数据进行处理并根据处理之后的数据对农产品价格波动的周期进行划分。顾国达、方晨靓[8]考虑国际市场因素对我国农产品价格波动的影响，选取国际农产品价格、美股市场、主要能源价格等指标，采用马尔科夫局面转移向量误差修正模型(MS-VECM)进行实证分析，实证结果表明我国农产品价格波动的局面转移特征较为明显、价格波动存在上涨迅猛但下跌缓慢的特征。

综上所述，对农产品价格波动的研究，目前学者主要聚集于价格波动成因的探索及价格在各环节传导机制的模拟，但根据农产品价格波动的周期性特征，对价格波动周期的非对称性研究并不十分深入。基于此，本文在利用B-P滤波分析农产品价格周期性特征的基础上，用非对称GARCH族模型深入研究农产品价格波动的非对称性特征。

二 农产品价格波动周期性测度

农产品价格波动的非对称性可以表现在许多方面，本文拟从两个层面进行分析：一是以农产品价格波动的周期性为基础，分析其周期长度(频率)和振幅上的非对称性；另一个层面是分析农产品价格波动时间依赖上的非对称性，即价格波动随着前期的波动程度大小而变化，也就是通常说的波动集群性。

数据的选取以中国人民银行网站公布的月度农产品价格指数为依据，考虑数据的可得性和有效性，取样的时间限定在1999年1月至2012年9月的农产品价格指数。进行定基化处理以后，以时间为横坐标，以相对应月份农产品价格指数的对数值(此时取对数值是为了在一定程度上去除数据的异方差性并和后文实证数据保持一致)为纵坐标绘制月度农产品价格指数的时间序列变化如图1所示：

从图1可以看出我国农产品月度数据呈现稳中有升的趋势，1999年到2003年期间，我国农产品价格波动呈平稳并且有略微下降的趋势，2003年1月农产品价格指数达到最低，之后开始一定程度反弹，保持持续增长状态值。2008年6月达到一个小高峰，在2009年1月达到短期谷底并开始新一轮的持续增长。

为了对农产品价格波动周期进行划分，本文采用B-P滤波法进行描述。B-P滤波法最早是由Baxter和King提出。该方法的基本思路是确定序列波动可能持续的时间长度，去除较高以及较低频率的波动。通过对权重的调节使最佳滤波和大致最佳滤波的平方差达到最小。当频率为0时，滤子的取值为0，从而尽量保持平稳时间序列的特征。

图1 农产品价格月度指数

yt=∑wjxt-jj∈(-,+)

其中，wj是确定的权重序列。

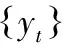
w(λ)=W(e-iλ)=∑wjeijλj∈(-,+)。

w(λ)为滤波的频率响应函数，通过对权重序列的适当设定，可以使某些区间内的w(λ)等于或接近于0，在此基础上将农产品价格波动区间内的分量“过滤”掉，留下农产品价格波动的主要成分。本文采用以1999年为基的预处理后的数据，得到中国农产品价格波动周期情况如图2所示：

图2 中国农产品价格波动周期

结合月度农产品价格时序图1和B-P滤波显示的结果图2可以将我国农产品价格波动分为四个周期阶段，如表1所示：

从总体波动特征看第一阶段(1999.1～2003.2)的价格波动为平稳时期，第二(2003.3～2006.8)、三(2006.09～2009.7)、四(2009.8～2012.9)阶段价格上升明显，四个阶段的周期振幅均表现出非对称性特征。分阶段数据的描述性统计量如表2所示：

表1 分阶段波动周期和振幅

表2 分阶段描述性统计量

三 农产品价格波动非对称性的检验

(一)农产品价格波动非对称性描述与理论模型形式

从农产品价格波动的时间序列图和周期性特征都可以发现，农产品价格波动在形式上具有非对称性特征，而这种非对称性需要通过统计检验才能确认。为了进一步检验其非对称性，本文采用同样的数据，先对转换以后的数据进行描述统计和平稳性检验，其结果如表3所示。

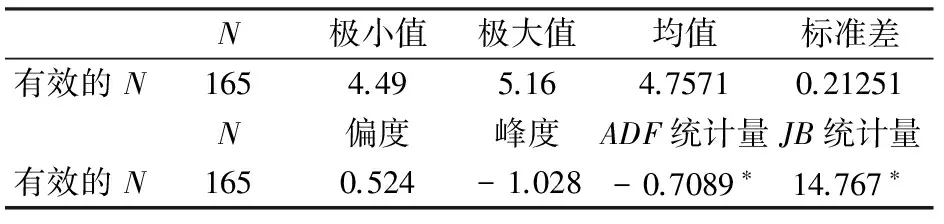
表3 中国农产品价格波动描述性统计量及平稳性检验

*表示1%显著性水平下显著。

转换后的农产品价格指数序列，其峰度和偏度系数均远大于3和0，有肥厚的尾部。且JB统计量在1%的显著性水平下拒绝农产品价格指数服从正态分布的假定。由于农产品价格指数的月度数据属于时序高频数据，容易产生异方差性，可对其先取对数，用对数数据进行分析或建模，减少一定的异方差性。然后设定均值方程并进行ARCH-LM检验，最后建立非对称类GARCH模型。这一处理符合非对称类GARCH模型的建模条件。

以EGARCH模型为例，即指数GARCH。该模型由Nelson在1991年提出，并对模型残差进行了更大程度的扩展。

其均值方程：

Log(apt)=C+r×log(apt-1)+ht

(1)

其条件方差模型：

(2)

式(2)左边是条件方差的对数，意味着杠杆影响是指数的而不是二次的，所以条件方差预测值是非负的。杠杆效应的存在通过γk得到验证，只要γk≠0，冲击的影响就存在非对称性。农产品价格市场正面消息和负面消息对模型条件方差有不同的影响：正面消息有一个αi的冲击；负面消息有一个对αi+γk的冲击。如果γk≠0，则农产品价格波动对市场信息冲击的反应是非对称的[9-11]。

(二)农产品价格波动非对称性的实证检验

本文用与上述同样的样本数据，采用一致性的数据转化方式，对农产品价格波动非对称性进行实证检验，模型基本形式为式(1)与式(2)，对其进行参数估计结果如表4所示。

从表4可以看出模型拟合效果很好，修正后的R2达到99.29%；HQ统计量值-5.31较小，说明模型总体拟合效果显著；在5%显著性水平下，各项系数均通过Z-Statistic检验，模型各项拟合通过。且1、2显著不为零，即该模型存在两个非对称性点。

表4 模型系数及其检验表

*表示5%显著性水平下，系数通过Z统计量检验

为了检验农产品价格波动非对称性的有效性，本文继续对拟合以后的模型残差进行ARCH检验。对GARCH类模型，Engle在1982年提出了检验残差序列是否存在ARCH效应的拉格朗日乘数检验(ARCH-LM)。由于忽略ARCH效应的影响可导致标准OLS估计的有效性降低，所以ARCH-LM检验可以帮助我们检验并提升模型估计的有效性。

对农产品价格波动模型的残差进一步拟合回归：

(3)

对此回归用F和Engle LM两个统计量进行检验。前者是对残差平方的滞后联合显著性所做的一个省略变量检验，其样本分布未知；后者一般情况下渐进服从自由度为p的卡方分布，检验结果如表5所示。

表5 ARCH检验结果Heteroskedasticity Test: ARCH

表5显示：拟合后的EGARCH模型，其F统计量和Engle LM统计量均小于0.05，对应的P值分别为0.946和0.945，大于5%显著性水平，显著拒绝原假设，即残差不再有ARCH效应。EGARCH模型的残差信息已提取充分。

四 农产品价格波动非对称形式

通过上述分析，农产品价格波动具有非对称性的特征，其非对称性用GARCH族模型基本上都可以刻画，但GARCH族模型具有不同的形式，基于此，本文对不同的条件方差模型进行比较，更为客观地描述农产品价格波动的非对称性，且有利于确认农产品价格波动的稳健性。

从农产品价格波动的非对称形式来看，一般可以由EGARCH、TGARCH 、和CGARCH三类模型进行描述，EGARCH模型形式前面已有阐述，在此不再赘述，只是对TGARCH和CGARCH两种模型形式进行简要说明。

TGARCH 模型又称门限(Threshold)GARCH模型，由Glosten，Jagannathan(1993)和Zokoian(1994)提出，其具体形式如下：

均值方程：

Log(apt)=C+r×log(apt-1)+ht

(4)

条件方差：

(5)

式(5)中dt-k为虚拟变量，当农产品价格市场有负面消息冲击即t-i<0时，dt-k=1，否则，dt-k=0。如此，农产品价格市场正面消息t-it-i<0)对模型条件方差有不同的影响：正面消息有一个的冲击；负面消息有一个对+的冲击。如果γ≠0 ，γ>0 ，则价格市场存在杠杆效应，非对称效应的主要效果是使得价格波动加大；如果γ<0 ，则非对称效应的作用是使得价格波动减小。

CGARCH模型允许条件方差的均值趋近于一个变动的水平：

东京国立博物馆藏有罗振玉旧藏敦煌本《刘子》残卷。此外还藏有一些敦煌写本和绢画，如《摩诃般若波罗蜜经》卷三十三高弼写本，系购自1926年东京古典籍下见展观大入札会；一些绢画则来自与法国集美博物馆的馆际交换，原为伯希和携自敦煌的艺术品。

qt=ω+ρ(qt-1-ω)+

(6)

(7)

只要γ≠0，冲击就会对农产品价格变化的短期波动产生非对称的影响。在CGARCH模型中，农产品价格变动的非对称性只体现在短期波动中，对价格长期波动率的影响则主要体现在系数的变化上。用三种模型形式对其进行参数估计，得到结果如表6所示。

表6 多种条件方差模型结果比较

*表示5%显著性水平下，系数通过Z统计量检验

为进一步考察农产品价格应对市场信息的冲击情况，下文绘制EGARCH模型的冲击曲线进行研究。

根据样本区间Sample(adjusted)：1999M02-2012M09，利用EGARCH模型的系数、1、2，通过以下命令生成序列s：

Serieslog(s)=γ×abs(zz)+α×zz

因本文设置了Asymmetric为2，得到两个门限系数α1=-0.574，α2=0.293

Serieslog(s)=0.638×abs(zz)-0.574×zz

Serieslog(ss)=0.638×abs(zz)+0.293×zz

Serieslog(sss)=0.638×abs(zz)-0.574×zz+0.293×zz

以序列zz为横坐标，序列s为纵坐标，得出非对称信息冲击曲线如图3所示。

从图3可以更为直观的看出，该信息冲击曲线具有明显的非对称性特征。从拐点对应的横坐标可以看出此模型具有两个非对称点。

五 基本结论

(一)农产品价格指数波动的振幅和周期均存在非对称性

农产品价格波动表现出一定的周期性，这种周期性与众多影响因素有关，而从市场供需来看，与农业生产周期理论上具有相关性或者一致性。而由于市场的干扰，流通环节囤积等市场行为的发生，使得周期波动的频率和幅度均出现不一致，主要表现在时间长短和时间前后的滞后性。按照农产品价格指数时序图体现出来的数据特征，进一步运用B-P滤波法将农产品价格波动整理为四个周期阶段，即第一阶段的平稳期和第二、三、四阶段的价格上升期。四个阶段的周期频率和振幅均表现出非对称性。

(二)农产品应对市场信息冲击非对称性

农产品价格波动对于不同的政策干预和信息冲击具有不同程度的反应。“正面消息”对农产品市场的刺激作用仍然需要其他市场干预的配合才能发挥出来。而市场上的“负面消息”，可以直接通过市场传播进而影响消费者对未来经济的预期。我国价格市场波动对市场信息的非对称反应模式，不仅可以揭示我国经济市场的风险特征，也可以解释消费者的风险管理行为。在非对称EGARCH模型的实证分析中，得到非对称项系数显著不为零，且有两个非对称点，验证了农产品对市场信息冲击具有非对称性，同时也为我国的农产品市场的宏观政策制定提供参考性依据，是否要加强“正面消息”加强“政策救市”、政策的执行力度和程度要如何把握等。

图3 农产品价格指数的信息冲击曲线

(三)农产品价格指数波动稳健性

本文采用多种形式的条件方差模拟样本区间数据，来描述和检验市场信息冲击对农产品价格波动的非对称性，以便验证所获结论的稳健性。多种形式的非对称GARCH族模型通过同一数据得到一致的实证结论，模型的非对称项系数均通过显著不为零的统计检验，得到一致的结论，证明了我国农产品价格指数波动是具有稳健性的，而不是特例现象。

[1] 李圣军,李素芳,孔祥智.农业产业链条价格传递机制的实证分析[J].技术经济,2010，(1):108-112.

[2]Benavides,G；PriceVolatilityForecastsforAgriculturalCommodities:AnApplicationofHistoricalVolatilityModels,OptionImpliedandCompositeApproachesforFuturesPricesofCornandWheat[M].CentralBankofMexico, 2004.

[3]Mitra,S.ANonlinearCobwebModelofAgriculturalCommodityPriceFluctuations[D].DepartmentofEconomics,FordhamUniversity, 2008.

[4] 顾国达,方晨靓.农产品价格波动的国内传导路径及其非对称性研究[J].农业技术经济,2011，(3):13-18.

[5]Meyer,J.andv.Cramon-Taubadel,S.AsymmetricPriceTransmission:ASurvey[J].JournalofAgriculturalEconomics，2004,(3):581-611.

[6] 胡华平,李崇光. 农产品垂直价格传递与纵向市场联结[J].农村经济问题，2010,(1)：11-13.

[7] 徐高雪. 农产品价格波动的影响因素及发展趋势[J].农业经济展望,2008,(2):24-27.

[8] 顾国达,方晨靓.中国农产品价格波动特征分析[J].中国农村经济,2010,(6):68-70.

[9]DimaAlberg,HaimShalit,RamiYosef,et.al.EstimatingstockmarketvolatilityusingasymmetricGARCHmodels. [J].AppliedFinancialEconomics, 2008,(18):1201-1208.

[10]Bollerslev,T.Aconditionallyheteroskedastictimeseriesmodelforspeculativepricesandratesofreturn.[J].ReviewofEconomicsandStatistics, 1987,(69):2-7.

[11] 刘汉中.具有GARCH( 1,1)-正态误差项的非对称单位根检验研究[J].统计研究，2007，(11)：75-77.

AResearchonAsymmetricPriceFluctuationofAgriculturalProducts

LI Zheng-hui, XU Ya-li

(College of Finance and Statistics, Hunan University, Changsha 410082, China)

Through the B-P filtering method, our country’s fluctuation of agricultural products price during 1999-2012 can be divided into four periods, which showed obvious unrepeatability and asymmetry characteristics. To combine descriptive statistical analysis with empirical analysis using asymmetric GARCH class models, the result verifies that asymmetry in agricultural product price fluctuation exists. And asymmetry has through statistics and economic test of the models. Empirical process shows that asymmetry of agricultural product price fluctuation has robustness characteristics and EGARCH can describe this asymmetry more effectively. Finally draw market information impact curve of EGARCH model to further verify the conclusion.

agricultural products; price fluctuation; asymmetry

2013-10-25

国家社会科学基金项目(12BTJ012)；教育部新世纪优秀人才支持计划(NCET-12-0173)；博士后基金项目(2013M531777)

李正辉(1974—)，男，湖南衡阳人，湖南大学金融与统计学院教授，博士生导师，博士.研究方向：风险管理与金融统计；宏观经济统计.

F322

A

1008—1763(2014)01—0053—05