测试性预计方法综述

刘 刚， 黎 放

(1.海军工程大学 管理工程系， 湖北 武汉 430033； 2. 海军工程大学 舰船综合保障工程研究室， 湖北 武汉 430033)

测试性预计方法综述

刘 刚1,2， 黎 放1,2

(1.海军工程大学 管理工程系， 湖北 武汉 430033； 2. 海军工程大学 舰船综合保障工程研究室， 湖北 武汉 430033)

分析了国内测试性预计的现状及存在的问题，研究了测试性预计模型。探讨了6种用于不同情况的测试性预计方法，前2种方法是基于装备功能结构的预计方法，中间3种方法是综合考虑装备故障、测试相互关系的方法，第6种方法是分析带BIT的装备虚警率预计的方法，并对这6种方法的特点和使用条件进行了分析，这些预计方法对于产品工程设计都有一定的指导意义。

测试性 预计 模型

1 引言

测试性是产品能及时准确地确定其状态(可工作，不可工作，性能下降)和隔离其内部故障的一种设计特性，是装备开展测试工作的基础[1]。测试性预计是为确定产品测试性参数是否满足规定测试性要求而开展的一系列分析和估计工作[2]。测试性预计一般需依照产品设计的相关资料，运用合适的模型或方法来分析并计算产品测试性指标，如故障检测率FDR、故障隔离率FIR、虚警率FAR等，从而判断产品测试性指标是否满足设计任务书的要求，以及测试性设计的难易程度及充分程度，并根据这些分析来判断产品设计存在的薄弱环节，是否需改进或完善设计。测试性预计工作可为评价不同设计方案提供依据，是产品开展测试性设计工作的重要依据。

当前，科学技术发展迅猛，使得装备设计也越来越复杂。装备性能得以提升，但也给装备保障带来了困难，为了提高装备战备完好性，以及便于开展维修工作，要求装备应具有较高的测试性水平。因此，在装备论证、设计研制阶段必须开展一系列的测试性分析与设计工作，确保装备达到规定的测试性水平，测试性预计就是这些分析与设计工作的重要组成部分。但当前测试性预计工作缺少相应的标准，同时研究测试性预计方法的研究文献也较少，使得该项工作的开展困难重重，缺乏相应的工程实际经验和理论研究。针对测试性预计工作现状，文中系统地收集并分析整理了国内外关于测试性预计的方法，并调研了国内测试性预计方法的实际应用情况，为开展测试性预计工作及相应标准规范的制定提供了理论依据。

2 测试性预计模型

开展测试性分配与预计工作，必须是建立在系统物理模型和数学模型的基础上。物理模型是描述系统组成结构关系的功能框图，是开展分配与预计工作的基本依据。在功能框图中，每个方框都有明确的定义及清晰的说明，框图的绘制需根据系统具体的结构和工作的需要。同时，为了便于开展测试及维修工作，通常将系统或子系统划分为外场可更换单元(LRU)，LRU再划分为车间可更换单元(SRU)或部件。数学模型是用一系列数学公式描述系统测试性，反映系统测试性指标与其下层设备测试性指标的关联关系。

进行测试性预计时，系统的故障检测率为

(1)

式中：λi为第i个故障模式的故障率；λS为所有故障模式的总故障率；γFDi为第i个组成单元的FDR值；γFDs为系统FDR值；λS为系统故障率。

系统的故障隔离率为

(2)

式中：γFIs为系统FIR值；γFIi为第i个组成单元的FIR值；λDs为系统可检测的故障率(λDs=λsγFDs)；λDi为第i个组成单元可检测的故障率(λDi=λiγFDi)。

系统的虚警率为

(3)

式中：γFAS为系统FAR值；γFAi为第i个组成单元的FAR值。

3 测试性预计的几种主要方法

3.1 传统工程方法

传统工程方法开展测试性预计工作是一个自下而上、由局部综合到整体的过程，开展这项工作，必须详细分析系统的组成结构，认真分析系统最底层组成部分的所有故障模式，然后再分析其检测、隔离工作如何开展，虚警如何控制等；接下来就由SRU到LRU逐一进行分析，直至系统约定层次；最终综合得出系统总的测试性水平。传统工程方法开展测试性预计工作的一般步骤如下所示：

(1) 分析系统设计资料及组成结构，并绘制出系统功能框图；

(2) 获取系统各组成部分的故障模式、故障率等数据；

(3) 分析及明确系统开展检测与隔离工作的具体方式；

(4) 分析及明确虚警的相关控制手段；

(5) 整理系统的分析结构及获取的数据，并填写测试性预计工作单；

(6) 计算系统的故障检测率与故障隔离率。从部件及LRU先开始计算，然后再计算系统的预计指标；

(7) 比较计算所得的预计值与要求值，如果达到要求值，则预计工作结束；如果没有达到要求值，应开展一系列改进工作并重新开展预计，直至达到要求值。

3.2 基于多信号模型的预计方法

基于多信号模型的预计方法是运用TEAMS(TestabilityEngineeringandMaintenanceSystem)软件来开展测试性预计工作。该方法依次从部件、子模块、模块、SRU、LRU、子系统、系统等逐级开展建模工作，然后从仿真角度描述同级之间及各级之间的功能关系[4～7]，其中模型的基本要素还包括功能模块(module)、模式转换开关(switches)、测试(test)、测试点(testpoint)、故障传播关系(dependencies)等。基于多信号模型的预计方法的基本步骤如下：

(1) 获取系统设计相关的资料，并挑选出与建模相关的元素；

(2) 建立系统功能结构模型，自下而上逐级展开；

(3) 明确所有模型的故障模式及其故障传播方式，构建故障模式与模块的关联关系；

(4) 明确所有模型的测试点，并明确各测试点的具体的测试方式；

(5) 明确系统的故障源及故障信息，以及与测试的关系；

(6) 开展各模型的测试性分析工作，并不断修改及完善；

(7) 评价所得的预计结果，将其与系统要求值进行比较，如果不能满足要求，则需对模型进行修改或升级。

3.3 概率方法

概率方法开展预计工作时，假设系统的检测事件是相互独立的。

由于系统结构不同以及部件、LRU数量的不同，相关逻辑关系也是不同的，随着系统结构越来越复杂，部件、LRU数量越来越多，求解测试性预计指标的公式也越复杂。因此，文中仅介绍考虑部件、LRU单一故障类的简单情况，其他复杂情况以此类推。假设系统故障类F1由测试1检测总是不正常，或者由测试2检测不正常而测试3检测正常，即Fi用三个测试进行诊断，按各测试输出是正常或不正常(通过或不通过)，可得出逻辑变量d和t的逻辑关系d=t1+t2t3，其中：ti为测试i的输出，其取值为1或0，i=1,2,3。测试不通过，ti已发生时为1；否则为0。各ti之间用逻辑或(加号)或者逻辑与(乘号)连接。d为诊断输出。d=1时，诊断输出为“真”，表示d已经或将会发生，能够诊断出故障。

在概率方法中，把所有的百分数作为概率处理，即故障类F1导致d=1的百分数被认为是F1发生时给出d=1的概率，或者表示为P(d=1|F1)。f1i被认为是F1发生时给出测试输出ti发生的概率，或者表示为P(ti=1|F1)。根据P(ti=1|F1)计算P(d=1|F1)时需要重复应用有关的标准概率公理和定理[8]。

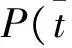
把②的结果代入③，并转到符号f1i，则

FDR=P(d|F1)

(4)

FIR指标的预计也可以用类似方法求解。

3.4 集合论方法

在概率方法中，测试是相互独立的，而集合论方法是不需考虑测试独立假设的。按照测试是否重叠，FDR的预计分以下3种情况：

(1) 专用测试的FDR。

假设测试输出t1和故障类Fj存在着一对一的对应关系，仅在Fj中某故障发生时，才有ti=1(即只有专用的测试功能)，fij表示发生故障Fj时，对应开展测试输出ti的概率。除非i=j，fij≠0(即所有故障类是不相交的)，且至少有一个ti=1时，检测才发生。对于有N个故障类的情况，用下式计算，即

(5)

得到各设备、分系统的FDR后，利用测试性预计模型求出系统的预计指标。

(2) 测试重叠覆盖的FDR。

在大多数现代测试性设计中，普遍有效地使用了功能测试和重叠BIT技术，专用测试的情况是非常少的，大部分的测试都是相互重叠的，而测试重叠又分为判断逻辑为加和判断逻辑为乘这两种情况。

假设存在单一故障类Fi，令d=t1+…+tj+…+tN，即判断逻辑为加，使d=1的故障的百分数称为FDR，则：

(6)

令d=t1…tj…tN，即判断逻辑为乘，使d=1的故障的百分数称为FDR，则：

(7)

得到各设备、分系统的FDR后，利用测试性预计模型求出系统的预计指标。

(3) 故障不相交和相交的FDR。

前面两种方法讨论的是测试是否重叠的情况，工程实际中还存在故障是否相交的情况，这时对FDR也是有影响的。

① 故障不相交的情况。

对于故障不相交的情况，可以对每一类故障计算其中引起诊断输出的故障的百分数进行分析，设这些百分数为fi。一般情况下，对应每个fi的范围是知道的，即fi=[Li,Hi]。如果所有故障类是不相交的，则容易给出FDR的范围(区间)：

(8)

② 故障相交的情况。

当包含相交故障时，给出两个相交故障类F1和F2，其失效率分别为λ1和λ2，且给出每类故障中导致相应诊断输出d=1的故障百分数f1和f2，则总的导致d=1的故障的百分数FDR由下式给出，即

(9)

式中：Nmax=max{λ1f1，λ2f2}；Nmin=min{λ1f1，λ2f2}；λmax=max{λ1，λ2}。

对于FIR的预计，集合论方法没有给出新的计算公式，仅仅对传统工程方法的计算组合。

3.5 基于贝叶斯网络的预计方法

基于贝叶斯网络的预计方法是在概率方法的基础上进行改进的，是运用贝叶斯网络模型求解系统故障与测试关系的预计方法。贝叶斯网络最早由Pearl在20世纪80年代系统地提出，又被称为贝叶斯信度网，是一种对概率关系的有向图描述，能够很好地解释系统的结构和行为特点，并做出图形化的描述[9～11]。

该方法也是自下而上进行的，首先计算部件Ci有故障时，与其对应的检测判据Ji(或隔离判据Li)能够正确或错误判断的概率，即Pr(Ji|Cj)。假设Ji为0～1判据，其取值为

(10)

因此，运用贝叶斯网络开展系统故障检测率与故障隔离率预计的数学模型如下所示。

(1) 故障检测率模型。

故障检测率的数学模型为

(11)

式中：λD表示被检测出的诊断模式的总诊断率；λ表示所有诊断模式的总诊断率；λi表示第i个被检测出的诊断模式的诊断率，mdl表示分析所用的诊断模型；lvl表示诊断模型所处的级别。

同时，单诊断模式Di(或Ci)的故障检测率为

FDRi=Pr(Ji=1|Ci=1)

(12)

因此，系统故障检测率预计的数学模型如下所示：

(13)

(2) 故障隔离率模型。

在开展计算之前，首先必须明确UUT的隔离模糊组，并假设这些模糊组是相互独立的。模糊组由i个诊断变量所组成。因此，模糊组AGi的故障隔离率如下所示：

(14)

式中：λD表示模糊组AGi中的被隔离的诊断模式的诊断率；Dj表示AGi中的第j个被隔离的诊断模式的诊断率。

故障隔离率预计的数学模型如下所示：

(15)

3.6 虚警率预计方法

虚警率是指按测试装置显示的产品故障状态与其实际所处状态不符合的概率。它由产品的工作环境、产品的稳定性、其他综合因素等决定[12]。目前，在开展测试性预计时，故障检测率、故障隔离率的预计方法已较为成熟，然而由于虚警率没有具体的数据，给开展预计带来了很大的困难，很难通过定量方法来对其进行研究，所以虚警率预计工作几乎没有开展。

假设BIT正常工作概率为Pk，产品本身(即剔除BIT部分)正常工作概率为P0，其中可以通过产品失效率和等效任务时间来计算Pk和P0的数值。

因此，产品在进行BIT检测时，可以从以下3种情况进行分析：

(1) 将产品正常状态判断正确的概率P1为

(16)

(2) 将产品故障状态判断为正常状态的概率P2为

(17)

式中：Q0=1-P0。

(3) 将产品正常状态判断为故障状态的概率P3为

(18)

式中：Qk=1-Pk。

在实际工程应用中，当P2作为BIT判断依据时，产品使用方承担了这部分风险；而当P3作为BIT判断依据时，产品设计制造方应承担这部分风险。从理论上讲，双方承担的风险应该是相同的，因而P2=P3，即

(19)

通过式(19)，可以得到：

(20)

可以运用式(20)开展产品虚警率的预计工作。

4 测试性预计方法的特点及适用条件

以上6种预计方法的特点和适用条件如表1所示。

5 结束语

随着科学技术的不断发展，武器装备的设计也越来越复杂，采取传统的测试性预计方法开展设计工作是很困难的。因此，在工程应用中，应该根据实际情况，适当选取合适的方法，或者将几种方法综合运用，这样才能满足装备测试性要求。文中给出的几种测试性预计方法，各有特点，适用于各种不同情况，如果合理运用，可为装备设计人员开展测试性预计工作起到一定的参考借鉴作用。

[ 1 ] 刘刚，黎放，胡斌．基于相关性模型的舰船装备测试性分析与建模 [J]．海军工程大学学报，2012，4：46-51.

[ 2 ] 石君友. 测试性设计分析与验证[M]. 北京：国防工业出版社，2011.

[ 3 ] 田仲.测试性分配和预计[J].北京航空航天大学学报，1995，21(4)：13-17.

[ 4 ] 杨智勇，牛双诚，姜海勋. 基于多信号模型的测试性预计方法研究[J].微计算机信息，2009，16：268-269.

[ 5 ] 常少莉，时钟，胡泊. 基于虚拟仿真的测试性预计技术研究及应用示例[J].环境技术，2012， 2：37-41.

[ 6 ] Somnath Deb, Krishna R.Pattipati, Vijay Raghavan, et al．Multi-Signal Flow Graphs: A Novel Approach for System Testability Analysis and Fault Diagnosis[A]．Proc. IEEE AUTOTESTCON 1994[C]．1994：361-373．

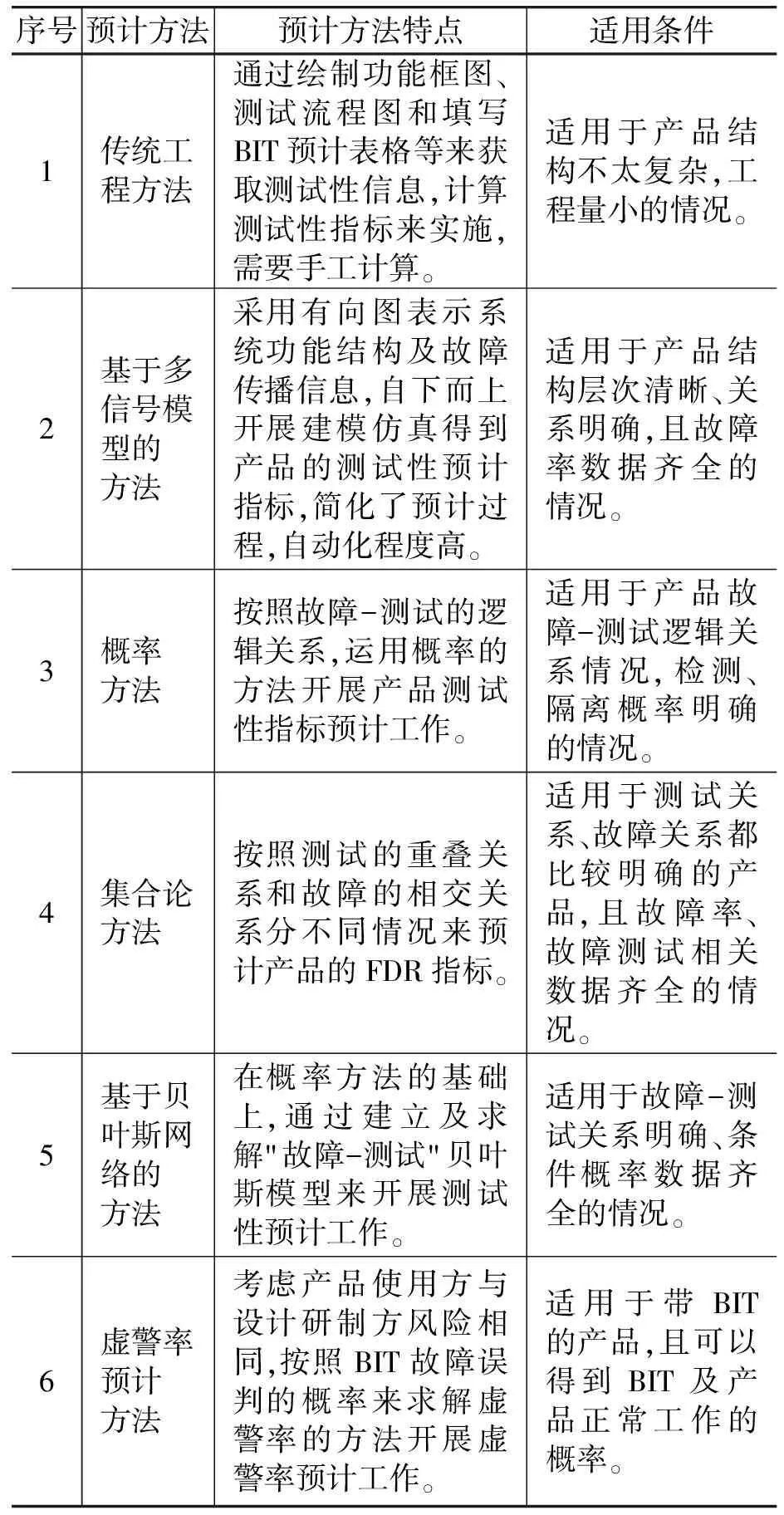
表1 测试性预计方法的特点及适用条件

[ 7 ] Qualtech Systems. Teams user guide[EB/OL].www.Teams QSI.com. 2003.

[ 8 ] 庄楚强，何春雄.应用数理统计基础 [M]. 广州：华南理工大学出版社，2013.

[ 9 ] Mark A Kaufman, John W Sheppard, Ph D. Bayesian Modeling: An amendment to the AI-ESTATE Standard[A]. Autotestcon 2005 Conference Record, IEEE Press[C].2005.

[10] 徐赫，王宝龙，武建辉. 基于贝叶斯网络的测试性预计方法[J].弹箭与制导学报，2007，27(4)：232-235.

[11] 李俭川.贝叶斯网络故障诊断与维修决策方法及应用研究[D].长沙：中国人民解放军国防科学技术大学，2002.

[12] 霍俊龙. 鱼雷测试性指标预计技术[C].中国造船工程学会年度优秀学术论文，北京：中国造船工程学会，2010.

Reviews of Testability Prediction Method

LIU Gang1,2， LI Fang1,2

(1.Dept. of Management Engineering, Naval Univ. of Engineering, Wuhan Hubei 430033, China; 2.Lab of Vessel Integrated Logistics Support, Naval Univ. of Engineering, Wuhan Hubei 430033, China)

The current situation and problems of testability prediction is analyzed, and prediction model is researched. Six kinds of methods for different circumstance of testability prediction are discussed. The first two methods are based on equipment’s function composition, the relationships between failure and test are synthetically considered in the middle three methods, false alarm rate of equipment within BIT is analyzed in the last method. Furthermore, the characteristic and application condition of the six methods is analyzed, and these methods are useful for products development.

Testability Prediction Model

国家部委基金资助项目(编号：4314231428)；海军工程大学自然科学基金项目(编号：HGDQNEQJJ13016)。

刘 刚(1982-)，男，讲师。

TP

A