快速计算平面与高精度细分曲面交线的方法

朱建宁，王敏杰，魏兆成，曹 斌

（大连理工大学 机械工程学院，辽宁 大连 116024）

0 引言

细分曲面建模法可以轻易构造具有任意拓扑结构的光滑曲面，广泛应用于计算机图形学、影视、动画等领域。曲面求交［1］是计算机辅助几何设计领域中的关键问题，其中平面与曲面求交是数控加工［2］、3D打印、快速原型［3］等领域中的基础问题。快速、稳定和高精度的平面与细分曲面求交技术有利于细分曲面在工业领域更广泛的应用。

由于细分曲面没有整体的解析表达式，在实际应用中，常常采用一定细分次数的控制网格代替细分曲面进行各种操作。理论上，一些平面与多边形网格求交的方法也适用于解决平面与细分曲面求交的问题。但在高精度细分曲面庞大的数据量和复杂拓扑结构的情况下，这种把细分曲面当作一般多边形网格的做法并不能获得较好的计算性能。在细分曲面之间求交的研究中，一些学者［4－7］利用二部图理论和局部细分技术，通过低层次控制网格之间相交区域的逐次求精，当控制网格的细分次数达到预设值时才进行细分曲面之间的求交。这类方法有效地控制了相交的网格边和网格面的搜索范围，提高了求交的效率。但这类方法也存在一定的局限性，由于控制网格的“收缩”特性，有可能会出现“多交”和“漏交”两种情况：低层次控制网格之间相交而细分曲面之间并不相交；低层次控制网格之间不相交而细分曲面之间相交。还有一些学者［8－9］基于细分曲面的参数化表示，研究了细分曲面求交和裁剪问题。在数控加工和快速原型等领域，为获得加工轨迹，常常需要对同一细分曲面模型与大规模平面组进行多次求交，显然上述一些求交方法的效率有待提高。

对于基于网格模型的求交计算，如何快速、准确和稳定地搜索出相交的网格边是最基础也是最重要的问题。高精度细分曲面庞大的数据量和复杂的拓扑结构，为高效搜索相交的网格边增加了难度。与现有方法不同，本文并没有把细分曲面当作一般多边形网格模型对待，而是利用细分曲面控制网格的拓扑结构特性，实现了 Catmull－Clark［10］细分曲面的分片表示，进而将平面与复杂细分曲面模型的求交问题转化为平面与形状简单的细分曲面面片的求交问题。针对平面与细分曲面面片求交问题，根据细分曲面面片规则的拓扑结构，分别建立细分曲面面片多级分割技术和交线追踪策略，以此为基础，快速、稳定地实现了平面与细分曲面面片的相交性判断和交线计算。

1 Catmull－Clark细分曲面的分片表示

Catmull－Clark细分曲面采用1～4面分裂的拓扑分裂规则生成新网格，属于四边形网格的逼近型细分模式。作为双三次均匀B样条曲面的推广，Catmull－Clark细分曲面具有良好的曲面连续性，除了在个别奇异顶点处为C1连续外，在其余各处均为C2连续。如果内部顶点的价（共享此顶点的边的数量）不等于4，则称该顶点为奇异顶点。Catmull－Clark细分模式生成的新点可以分为新面点、新边点和新顶点三个基本类型，对于边界情况，还有边界新边点和边界新顶点。图1给出了Catmull－Clark细分算法的细分模板，图中：新顶点由空心圆点表示，原网格顶点由圆点表示。

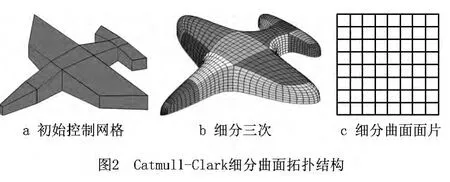
图2中的初始控制网格经过三次Catmull－Clark细分后，每个初始控制网格中的四边形面片都转变为呈方阵排列的四边形面片组，这样的面片组称为细分曲面面片（Subdivision Surface Patch，SSP）。不论拓扑结构多么复杂的Catmull－Clark细分曲面，都可以分解为若干个具有相同拓扑结构的SSP。这不仅是Catmull－Clark控制网格不同于一般多边形网格的拓扑结构特性，也是分片表示Catmull－Clark细分曲面的理论基础。

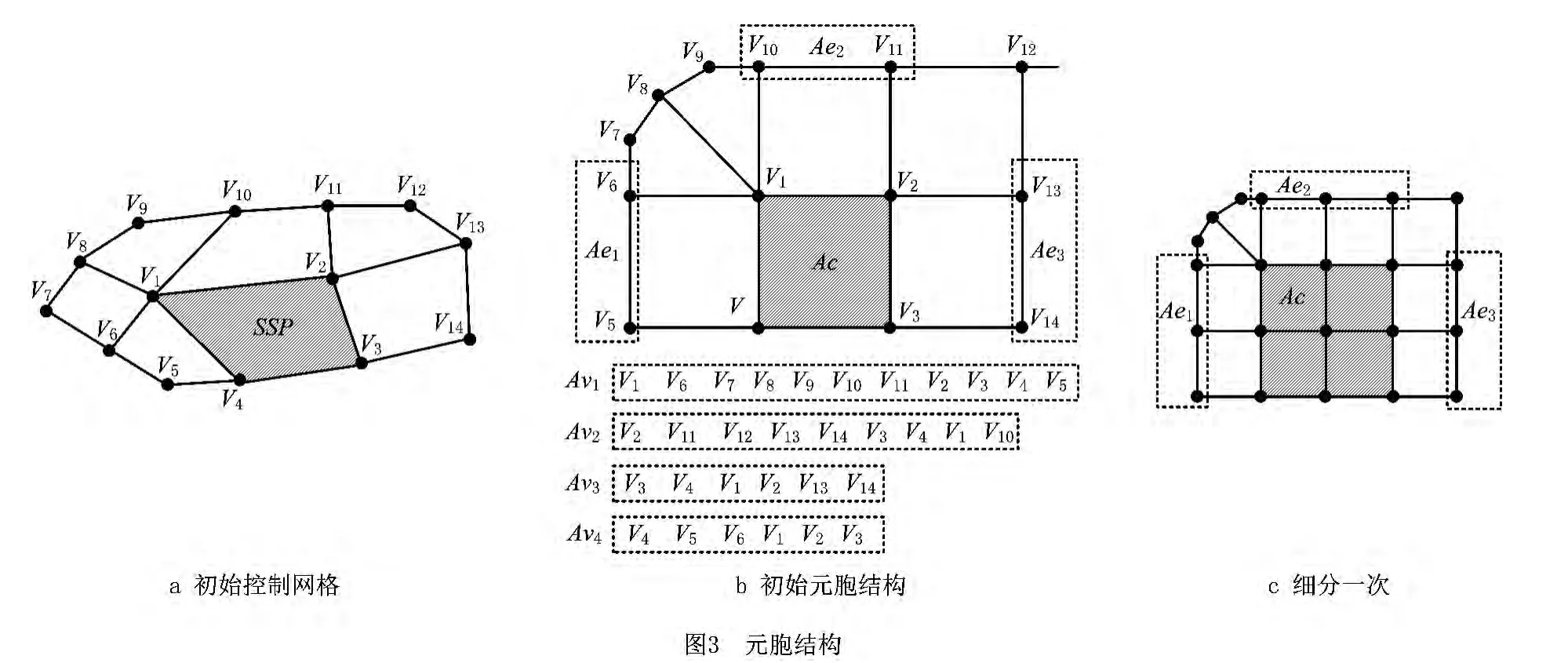
为获得更高的平面与细分曲面求交的计算性能，本文采用元胞结构［11］实现了细分曲面的分片表示。元胞内层结构由一个二维数组和若干个一维数组构成。二维数组表示SSP，称其为元胞数组（Ac）；一维数组表示SSP的邻域结构。根据邻域结构辅助细分作用的不同，可以将邻域结构分为辅助SSP边界细分结构（Ae）和辅助SSP角点细分结构（Av）。元胞外层结构可以采用半边结构，通过半边结构记录初始控制网格的拓扑结构来表示SSP之间的拓扑关系。如图3所示，图3a为带边界的SSP及其邻域结构所组成的初始控制网格，图3b表明了网格顶点与元胞内层结构的对应关系。其中：Av1，Av2，Av3和Av4分别为辅助SSP角点细分的结构，Ae1，Ae2和Ae3分别为辅助SSP边界细分的结构。应用元胞结构可以将Catmull－Clark细分曲面的整体细分转化为各个元胞的局部细分。图3c为初始元胞结构细分一次后的结构。这种分片实现Catmull－Clark细分曲面的方式并没有改变基本的细分规则，其中正确判断新点的类型并采用对应的细分模板，是确保元胞局部细分顺利进行的关键。

2 细分曲面面片多级分割

经过N次细分后，SSP网格的拓扑结构是一个大小为（2 N＋1）2的方阵，其中包含四边形面的数量为4N。如果把细分N次的SSP均匀分割为4个子面片，则每个子面片网格的拓扑结构都是大小为（2N－1＋1）2的方阵，其中包含四边形面的数量为4N－1，将这次分割定义为第一级分割。由此可见，细分N次的SSP进行第一级分割后，所获得的子面片网格的拓扑结构与细分N－1次的SSP网格的拓扑结构相同。同时，所获得的子面片可以进行下一级分割。对于细分N次的SSP可以进行N级分割，第M级分割最多可以形成4M个大小为（2N－M＋1）2的方阵网格。SSP多级分割结合轴对称包围盒（Axis Aligned Bounding Box，AABB）干涉检测技术，可以快速排除不与平面相交的分割子面片。通过相交子面片的逐级分割，不断缩小相交网格面的搜索范围。在该过程中，如果某一级分割后所有子面片的AABB与平面均不相交，则说明该SSP与平面不相交。SSP多级分割并不是真正分割网格，而是为了提取特定范围内的网格顶点创建AABB。由于SSP顶点的坐标存储在Ac中，通过确定Ac行列索引的取值范围就可以提取对应的顶点。多级分割的子面片采用如下公式表示：式中：二维数组An1，An2，An3和An4分别表示由第n级分割获得的四个子面片；in1，jn1，in2，jn2，in3，jn3，in4和jn4分别为对应二维数组的起始行列索引；ln为第n级分割子面片的二维数组中终止行列索引与起始行列索引之差；in－1和jn－1分别为第n级被分割面片的二维数组的起始行列索引；i0和j0分别为Ac的起始行列索引。因此，只要确定第n级被分割面片的二维数组的起始行列索引，就可以提取由第n级分割获得的四个子面片。图4所示为细分三次的SSP多级分割的具体过程，深色的子面片表示被分割的面片。

3 平面与细分曲面面片求交

平面与SSP求交可以分为以下三个步骤：①计算交线的起始交点并确定交线类型；②计算交线的后续交点；③判定交线的终止交点。

3．1 计算起始交点并确定交线类型

将平面与SSP交线的第一个交点定义为起始交点，图5所示的实心圆点即为起始交点。细分次数为N 的SSP中含有网格边的数量为22N＋1＋2N＋1。若直接提取SSP的网格边并与平面进行相交测试，则效率较低，特别是当SSP的细分次数较高时。在碰撞检测中，常常采用包围盒近似表示复杂物体，以提高碰撞检测的效率。结合平面与AABB的相交检测技术和SSP多级分割，计算起始交点的步骤如下：

步骤1 创建SSP的AABB，并与平面进行相交检测。如果平面与AABB不相交，则说明平面与SSP不存在交线，结束程序。

步骤2 提取SSP的边界网格边，并与平面进行相交检测。如果检测到与平面相交的网格边，则计算起始交点并结束程序。

步骤3 设置n的初始值为1，将SSP进行第n级分割。

步骤4 分别对获得的分割子面片创建AABB，并与平面进行相交检测。如果所有第n级分割子面片的AABB与平面均不相交，则结束程序。

步骤5 提取与平面相交的AABB中子面片的边界网格边，并与平面进行相交检测。如果检测到与平面相交的网格边，则计算起始交点并结束程序。

步骤6 如果n＜N，则N为SSP的细分次数，n＝n＋1，转步骤3。否则，结束程序。

根据起始交点位于SSP中的拓扑位置，可以把平面与SSP的交线分为两种类型：如果起始交点位于SSP的边界，则将此时的交线定义为线型交线；如果起始交点位于SSP的内部，则将此时的交线定义为环型交线。图5a和图5b所示分别为线型交线和环型交线。

3．2 计算后续交点

假设平面与四边形网格面存在两个交点，如果其中一个交点已知，则另一个待求交点可以称为已知交点的后续交点。根据交点的拓扑位置，可以将平面与四边形网格面的交点分为两种类型：①如果交点位于网格边的内部，则称其为边交点；②如果交点位于网格边的端部，则称其为点交点。为区分不同方位的交点，每种类型的交点还可以分为四种情况。当已知交点的具体类型和情况确定后，在四边形网格面中提取对应的网格边与平面进行相交检测，可以获得后续交点。当得不到后续交点时终止计算程序。如图6所示，圆点表示已知交点，线段表示对应的网格边，图6a～图6d描述了四种边交点对应的网格边的选取方法，图6e～图6f描述了四种点交点对应的网格边的选取方法。

当获得起始交点后，根据起始交点所属的网格面和起始交点的具体类型和情况，可以搜索出与平面相交的网格边并获得后续交点。根据后续交点可以确定下一个与平面相交的四边形网格面，而该后续交点成为求取下一个后续交点的已知交点。以此类推，可以采用递归的方式计算出平面与SSP交线中的所有后续交点，直到满足终止求交条件时停止计算。

3．3 判定终止交点

将平面与SSP交线的最后一个交点定义为终止交点，图5所示的空心方点即为终止交点。根据已知交点获得后续交点后，需判断后续交点是否为交线的终止交点。如果后续交点被判定为终止交点，就达到了终止求交条件，可以停止交线计算。根据交线的不同类型，采用不同的方法判定终止交点。对于线型交线，如果后续交点位于SSP的边界，则该后续交点即为终止交点；对于环型交线，如果后续交点与起始交点相同，则该后续交点即为终止交点。

3．4 算法复杂度分析

对于细分N次的细分曲面面片，顶点的数量为（2N＋1）2个，边界网格边的数量为4×2N个。因此，细分曲面与平面求交算法的复杂度为O（m×（2N＋2＋3n））。其中：m表示与平面相交的细分曲面面片个数，n表示细分曲面面片中与平面相交的网格边的数量。

4 算法描述

极限网格顶点是控制网格对应顶点的极限位置。对于逼近型细分模式，相同细分次数的极限网格比控制网格具有更高的表示精度。因此，以一定细分次数的极限网格代替细分曲面与平面求交，有利于降低计算机内存消耗和提高求交效率。由于相同细分次数的极限网格与控制网格具有相同的拓扑结构，极限网格同样可以采用元胞结构分片表示。可以采用 Halstead等［12］的方法获得Catmull－Clark细分曲面的极限网格，采用Huang［13］的方法计算满足一定精度的极限网格的细分次数。计算平面与细分曲面交线的算法步骤如下：

步骤1 根据用户指定的精度，计算Catmull－Clark细分曲面极限网格的细分次数。

步骤2 应用元胞结构实现Catmull－Clark细分曲面的分片表示。

步骤3 对每个SSP创建AABB。设置n为SSP的个数，i的初始值为0。

步骤4 i＝i＋1，如果i＞n，则中止计算程序并输出计算结果。

步骤5 判断第i个SSP的AABB是否与平面相交。如果不相交，则转步骤4。

步骤6 结合SSP多级分割，计算第i个SSP与平面的起始交点并确定交线的类型。如果没有获得起始交点，则转步骤4。

步骤7 计算后续交点。

步骤8 判断是否满足终止求交条件。如果不满足条件，则转步骤7。

步骤9 如果i＝＝n，则根据元胞外层结构描述的SSP之间的拓扑关系，合并平面与SSP的交线段，输出平面与Catmull－Clark细分曲面的交线，否则转步骤4。

平面与Catmull－Clark细分曲面求交的算法流程如图7所示。

5 算法测试与分析

算法测试共分为三部分：①主要测试平面与SSP求交的稳定性；②主要测试平面与复杂细分曲面模型求交的效率；③主要测试大规模平面组与复杂细分曲面模型求交的性能。算法测试的软、硬件环境分别为：Windows 7 64－bit操作系统和 MATLAB 2012b软件；CPU i5－3570k，RAM 4G。

第①部分算法测试的测试模型是一个细分10次的Catmull－Clark细分曲面面片。以图8所示的平面和SSP作为测试样本，各个测试样本中的平面与SSP的相交情况、交线类型、交点个数和算法耗时等测试数据如表1所示。

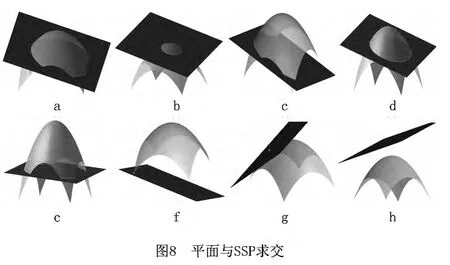
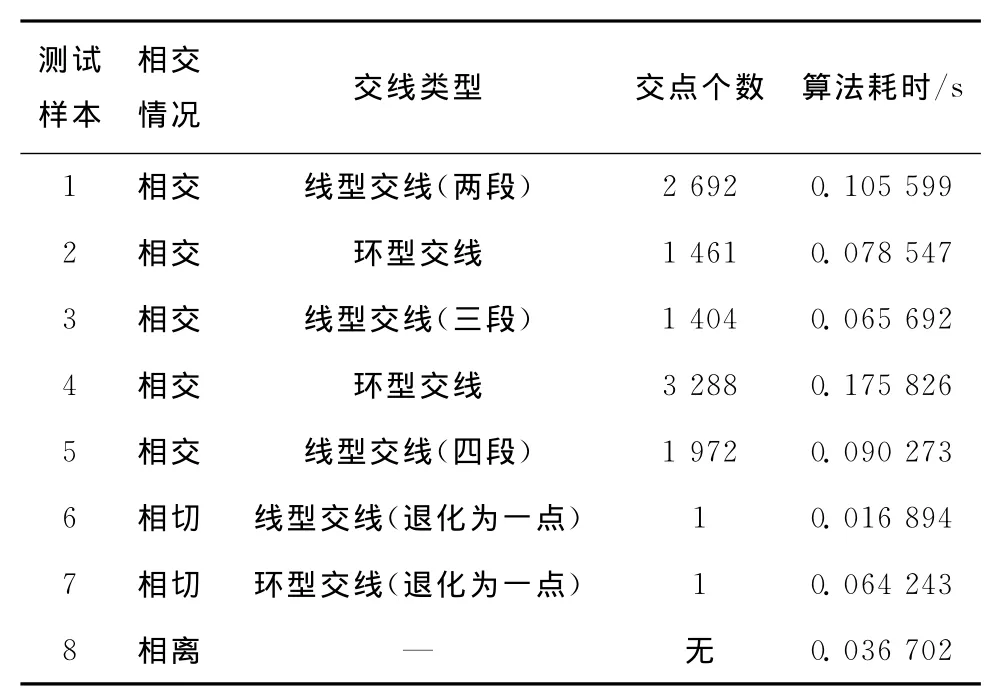
表1 测试平面与SSP求交的数据

从表1中的数据可以看出，对于图8所示的平面与SSP的相交、相切和相离的情况，算法均能给出正确的结果，测试结果表明了平面与SSP求交的稳定性较强。SSP是构成细分曲面模型的基本数据元素，理论上，平面与细分曲面模型在全局范围内的交线必然存在于局部SSP之中，因此将平面与复杂细分曲面模型的求交问题转化为平面与拓扑结构简单的SSP的求交问题，有利于提高平面与复杂细分曲面模型求交的稳定性。

第②部分算法测试的测试模型是细分9次的复杂细分曲面模型。以图9所示的平面和复杂细分曲面模型作为测试样本，各个测试样本的SSP个数、交点个数、SSP的AABB与平面相交的数量、与平面相交的SSP的数量和算法耗时等测试数据如表2所示。

表2 测试平面与复杂细分曲面模型求交的数据

从表2的数据可以看出，对于图9所示的平面与复杂细分曲面模型的相交情况，算法均能给出正确的结果。对于测试样本1和2，在测试模型的顶点个数达到五千万级的情况下，计算耗时为1．3s左右。测试结果表明平面与复杂细分曲面模型求交的效率较高。基于元胞结构分片表示Catmull－Clark细分曲面主要是为了在交线计算的过程中实施分治策略。以SSP的AABB与平面相交检测为基础的第一级分治可以快速排除绝大多数与平面不相交的SSP，显著降低了求交的规模，如表2所示，与平面相交的SSP的数量仅占测试模型SSP总数的一小部分。以SSP多级分割为基础的第二级分治可以快速计算起始交点，同时，针对SSP拓扑结构特性的后续交点计算方法在根本上提高了求交的效率。

第③部分算法测试的测试模型是一个由29个SSP构成的细分8次的复杂细分曲面模型。分别以图10a所示的飞机模型和垂直于X，Y，Z坐标轴的大规模平面组作为测试样本，针对平面垂直于坐标轴，在任意平面与细分曲面求交的基础上对算法进行了优化。各个测试样本的平面间距、平面个数、交点个数和算法耗时等测试数据如表3所示。

表3 测试平面与复杂细分曲面模型求交的数据

如图10b～图10d所示，算法均能给出正确的结果，从表3的数据可以看出，在测试模型的顶点个数近百万级和截平面的数量过百的情况下计算耗时均较低，测试结果表明以本文算法为基础的大规模平面组与复杂细分曲面模型求交的性能较高。这为细分曲面在数控加工、快速原型和3D打印等领域的应用提供了基础。

6 结束语

应用元胞结构分片表示Catmull－Clark细分曲面，不但有利于降低高精度细分曲面的计算机内存消耗，而且可为分治策略的实施提供基础。分治策略的实施将复杂细分曲面模型与平面求交的问题转化为简单细分曲面面片与平面求交的问题，不仅降低了求交的规模，还提高了交点计算的稳定性和效率。细分曲面面片多级分割结合轴对称包围盒干涉检测技术，可以快速判定平面与细分曲面面片的相交性和获得交线的起始交点。以起始交点为基础，针对细分曲面面片拓扑结构特性的后续交点计算方法，在根本上提高了平面与细分曲面面片求交的效率。通过实例测试了算法的稳定性和效率，测试结果表明本文提出的平面与Catmull－Clark细分曲面求交的算法实用、高效。如何将本文算法的核心理论和方法扩展到Catmull－Clark细分曲面之间求交的研究中，是未来的研究方向。

［1］ CHEN Xiaoxia，YONG Junhai，CHEN Yujian，et al．Intersection algorithm based on coordinate transformation［J］．Computer Integrated Manufacturing Systems，2005，11（9）：1327－1332（in Chinese）．［陈晓霞，雍俊海，陈玉健，等．基于坐标变换的曲线曲面求交算法［J］．计算机集成制造系统，2005，11（9）：1327－1332．］

［2］ LI Min，ZHANG Lichao，MO Jianhua，et al．Smoothing technique for 2Dcontour in numerical control plasma cutting［J］．Computer Integrated Manufacturing Systems，2011，17（12）：2623－2629（in Chinese）．［李 敏，张李超，莫健华，等．一种数控加工二维轮廓的平滑处理技术［J］．计算机集成制造系统，2011，17（12）：2623－2629．］

［3］ GAO Xinrui，ZHANG Shusheng，HOU Zengxuan．Three direction DEXEL model of polyhedrons and virtual rapid prototyping procedure simulation［J］．Computer Integrated Manufacturing Systems，2007，13（12）：2415－2420（in Chinese）．［高 新瑞，张树生，侯增选．多面体三向DEXEL模型与虚拟快速原型［J］．计算机集成制造系统，2007，13（12）：2415－2420．］

［4］ YUAN Hong，LIAO Wenhe．On Catmull－Clark subdivision surface intersection with a given precision［J］．Mechanical Science and Technology，2008，27（4）：486－489（in Chinese）．［袁

鸿，廖文和．给定精度条件下的Catmull－Clark细分曲面求交研究［J］．机械科学与技术，2008，27（4）：486－489．］

［5］ ZHENG Liyin，ZHANG Li．Study of intersections for subdivision surface with convex hull［J］．Computer Engineering and Design，2008，29（1）：102－104（in Chinese）．［郑立垠，张 丽．基于凸包特征的细分曲面求交研究［J］．计算机工程与设计，2008，29（1）：102－104．］

［6］ NASRI A．Polyhedral subdivision methods for free form surfaces［J］．ACM Transactions on Graphics，1987，6（1）：29－73．

［7］ LANQUETIN S，FOUFOU S，KHEDDOUCI H，et al．A graph based algorithm for intersection of subdivision surfaces［C］//Proceedings of the 2003International Conference on Computational Science and Its Applications．Berlin，Germany：Springer－Verlag，2003：387－396．

［8］ LI Tao，ZHOU Laishui．Research on intersection and trim－ming algorithms for subdivision surfaces［J］．Computer Engineering and Applications，2009，45（30）：177－184（in Chinese）．［李 涛，周来水．细分曲面求交裁剪算法研究［J］．计算机工程与应用，2009，45（30）：177－184．］

［9］ ZHU X P，HU S M，TAI C L，et al．A marching method for computing intersection curves of two subdivision solids［C］//Proceedings of the 11th IMA International Conference on Mathematics of Surfaces．Berlin，Germany：Springer－Verlag，2005：458－471．

［10］ CATMULL E，CLARK J．Recursively generated B－spline surface on arbitrary topological meshes［J］．Computer－Aided Design，1978，10（6）：350－355．

［11］ ZHU Jianning，WANG Minjie，WEI Zhaocheng，et al．An algorithm for quickly calculating the signed distance between apoint and a subdivision surface［J］．Computer Integrated Manufacturing Systems，2013，19（4）：687－694（in Chinese）．［朱建宁，王敏杰，魏兆成，等．快速计算空间点到细分曲面有符号最近距离的方法［J］．计算机集成制造系统，2013，19（4）：687－694．］

［12］ HALSTEAD M，KASS M，DEROSE T．Efficient，fair interpolation using Catmull－Clark surfaces［C］//Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques．New York，N．Y．，USA：ACM Press，1993：35－44．

［13］ HUANG Z，DENG J，WANG G．A bound on the approximation of a Catmull–Clark subdivision surface by its limit mesh［J］．Computer Aided Geometric Design，2008，25（7）：457－469．