三维正交机织复合材料力学模型研究进展

荆云娟

(天津工业大学，天津 300160)

三维正交机织复合材料力学模型研究进展

荆云娟

(天津工业大学，天津 300160)

文章针对细观结构和理论模型进行了综述和回顾，重点介绍了三维正交机织复合材料的分析模型，以期待为今后的研究工作提供借鉴。

三维正交机织复合材料；细观结构；理论模型

传统的纤维增强层合复合材料具有易分层，刚度、强度低，抗冲击性能差，损伤容限低等缺点，其主要是由厚度方向上的层合结构所导致,这些因素都阻碍了层合复合材料在航空航天等领域的广泛应用[1]。3D机织复合材料因其厚度方向增强纤维的存在，有效地改善了层合复合材料的一些力学性能，广泛应用于航空航天，航海，汽车，民用基础设施和医用领域中[2-3]。

三维正交机织复合材料作为三维机织复合材料中一个重要分支，其织造技术操作简单且成本低[4]。三维正交机织复合材料(3D orthogonal woven composite,简称3DOWC)由三个系统纱线组成，如图1所示，在面内经纱和纬纱不相互交织，呈0°和90°排列，提供了复合材料的面内性能，在面外Z向纱沿厚度方向交错捆绑外层纬纱，提供了复合材料的整体结构稳定性[2，5]。三维正交机织复合材料的这种特殊结构使其在一些力学性能方面优于其他结构的复合材料：与平纹层合板相比，其层间断裂韧性、拉伸强度、弯曲强度等要高很多；与角连锁织物相比，能在厚度方向上提供更大的纤维体积分数[6]。与此同时三维正交机织复合材料的力学性能受到诸多因素的影响，如纤维种类，基体类型、成型方式、织造参数、细观结构等，使得目前对3DWOC的研究结果多样化[7]。因此，本文针对这些影响因素对三维正交机织复合材料的力学性能进行回顾探讨，以期对未来的研究提供借鉴。

图1 3DOWC纱线系统示意图

1 三维正交机织复合材料的细观结构

三维机织复合材料的细观结构研究，是通过对其代表性体积单元(RVE)[8]进行细观分析，包括增强体中的纱线截面，纱线之间的相互交织情况(如：纱线走向，位移，尺寸等)，代表性体积单元的尺寸。三维机织物增强复合材料的力学性能主要由增强纤维及织物几何结构特性来决定，因此研究三维机织增强体的细观结构在力学性能研究中占有重要地位[9]。

对于纱线的截面形状，以Peirce[10]为首的许多研究者[11-16]相继提出了圆形，矩形，椭圆形，跑道形和双凸透镜形的假设如图2所示。这些截面形状都从不同程度上描述了织物中纱线的形态。

图2 纱线截面形状

(a)圆形，(b)矩形，(c)椭圆形，(d)跑道形，(e)凸透镜形

三维正交机织复合材料由于厚度方向捆绑纱的存在，使它具有一些优于其它结构复合材料的性能，如Ishikawa[17]等人指出3DWOC(碳纤维/环氧树脂)的层间断裂韧性比仅具有0.6%捆绑纱的层合复合材料大10或15倍。因此众多研究者[18-20]把注意力放在了捆绑纱的空间轨迹上，通过对材料断面显微照片的观察，经纬纱线基本呈直线状态，对于捆绑纱的路径形态，不同研究者则建立的捆绑纱模型不同，有矩形折线状态，正弦曲线状态，曲线与直线的结合，半圆与直线的结合等。捆绑纱模型如图3所示。其中矩形折线状态与实际结构存在差异较大。郭兴峰[21]提出的曲线与直线结合的捆绑纱模型，且越靠近织物中央，接结纬纱的直线部分越短，接结纬纱的捆绑效应使经纱产生聚集，且接结纬纱形状的变化造成织物的结构不均匀。Xuesen Zeng[22]使用计算机对3D正交机织物进行连续断层扫描，指出捆绑纱的路径随压缩水平的增加而发生变化，无压力情况下，捆绑纱呈轻微的“S”型，轻压下，捆绑纱屈曲增加，重压下经纬纱间距离减小，如图4所示。在TexGen中，为了考虑压缩水平对捆绑纱路径的限制，在不同织物层的纬纱表面放置一定数量的参照节点，来模拟捆绑纱的变形。

图3 捆绑纱轨迹图

图4 织物在压缩下纱线的几何变化

在实际的三维正交机织结构中，纬纱并不是如很多研究者所描述的呈直线状态，Z向纱也不是沿规则的路径捆绑纬纱的，它们都存在一定的屈曲形态，纬纱的屈曲存在会影响织物的面内性能，而Z向提供了整个织物结构的稳定性，这些因素都会影响到复合材料的性能。Leong[23]研究了捆绑纱屈曲形态对复合材料力学性能的影响,发现捆绑纱的非矩形折线分布降低了复合材料的强度。

2 三维正交机织复合材料(3DOWC)的理论分析模型

为了充分利用纺织复合材料性能可设计性的优势，减少材料实验的工作量，缩短设计周期，许多研究者建立了3D机织复合材料的力学分析模型，通过细观结构参数来预测材料的宏观力学性能。因此，建立一个能够在微观尺度上模拟纺织复合材料，预测其有效的力学性能的分析模型就变得至关重要[8]。

预测3DOWC弹性能性能的模型主要有层板理论，取向平均模型，等应力等应变混合模型，有限元模型等。

取向平均模型被很多研究者使用来预测代表性单元尺度上的2D和3D复合材料的宏观弹性性能。在取向平均模型中，复合材料的代表性体积单元被离散成小体积单元，其中所有的纤维在一个特定的方向上排列和取向，这依赖于增强相结构。每一个体积单元被看作是具有横向各向同性性能的单向复合材料。宏观性能通过在等应力或等应变假设条件下，对外载荷响应的平均值求得，取向平均模型没有考虑纱线波动的影响[8]。Hage[24]等采用取向平均法来预测3DOWC的弹性性能，得到预测结果与实验结果有较好的一致性。

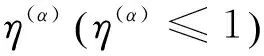
(1)

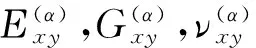
Buchanan等[26]提出了预测3D正交复合材料的弹性常数的分析模型。该模型在两个水平上划分复合材料的代表性体积单元，先是离散成正交各向异性片状(层状)，然后离散成条状(单元)，如图5所示。每一个条状(单元)由纤维和基体组成，看作是单向复合材料。并采取了等应力、等应变假设条件和面内应力条件应用于层状的假设，由单元的刚度集合计算出片状的刚度，再由片状刚度集合得出整体单胞的刚度。其中等应变假设用于纵向，等应力假设用于横向。该模型与取向平均模型和改进的取向平均模型相比，有很大的改善，比二元模型预测更准确，但因为该模型假设Z向捆绑纱是垂直贯穿织物(实际上并不是)，造成Ez值估计过高。该模型预测的弹性模量与实验值也吻合较好。

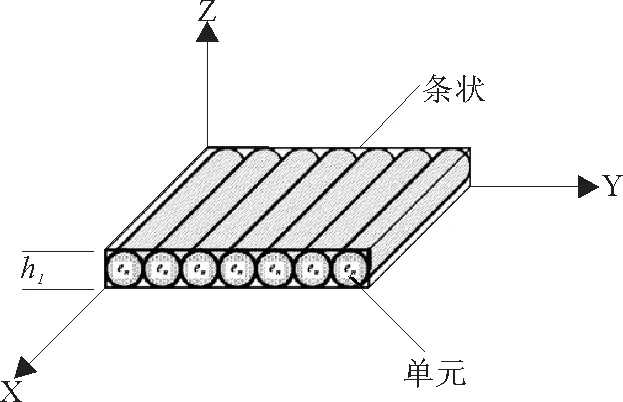
图5 整体坐标系下层内包含的单元

在层板理论和取向平均模型二者基础上，Huang等[27]提出了一种新的分析模型用来预测应用3DWOC复合材料的弹性性能。在该模型中，3D复合材料被当作是一个层合板并被分成薄片，每一层薄片包含经纱束和纬纱束，连同贯穿每层薄片的捆绑纱的一部分。在取向平均模型基础上，每层薄片的刚度由薄片内的纤维束集合来决定。由于变形的相互影响，累积每一层的性能来获得3D复合材料层合板的弹性性能。通过比较预测结果与实验结果，该模型得到验证，且二者之间有很好的一致性。

对于Tan[28]提出的等应力等应变混合模型即“XYZ模型、YXZ模型、ZXY模型和ZYX模型”，在这四个模型中，单胞内的三种纱线截面形状都为矩形，且单胞都被划分成许多矩形微块，如图6为XYZ模型的单胞示意图。这四种模型对刚性常数计算都是对“X模型、Y模型、Z模型”(图7)综合运用，如在XYZ模型中，带状I、II、III使用X模型计算，顶部和底部微块使用Y模型计算，单胞的整体刚性常数使用Z模型计算，结果表明在这四种模型中，使用ZXY模型和ZYX模型计算得到的Ε1、、Ε2、ν12、ν13、ν23和G12比XYZ模型和YXZ模型都有大，但预测Ε3值比后两者小，对于G23值，YXZ模型和ZYX模型预测值要比其余两种模型预测值小。

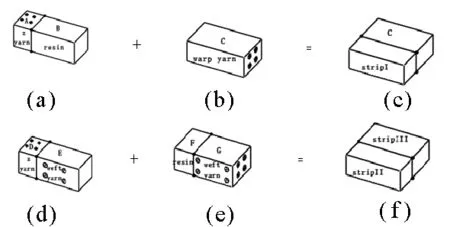
图6 三向正交机织物的“XYZ模型”示意图

图7 (a)X模型，(b)Y模型，(c)Z模型

有限元方法也被广泛用于研究3DOWC的弹性性能。Kim等[29-30]通过模拟材料测试，并进行大范围的有限元分析来预测3DWOC的弹性性能。所建单胞包括经纱、纬纱、捆绑纱和树脂区域组成，这些组分被划分成八节点固体单元。因为精确的有限元分析需要一个巨大自由度的网格建模，所以文中使用了并行多波求解器进行模拟实验。模拟结果与实验结果有很好的一致性，由以下给出的胡克定律等式决定弹性性能：

(1)

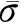
(2)

(3)

其中V是有限元模型的整个体积。

3 结语

国内外已经对三维正交机织复合材料的细观结构和理论模型的研究取得了较好的进展，但随着其应用领域的不断扩展和使用性能要求的进一步提高，对材料性能的预测精确性也提出了更高的要求。

对于细观结构的研究，所使用的理想几何模型不能很好地计算经纬向以及厚度方向上纤维的实际体积分数，因为通常增强体表面纬纱由于捆绑纱的作用是屈曲状的，捆绑纱也不是按照理想路径走的，所以为了准确计算各个方向上的纤维体积含量，以及为了更好地预测力学性能，有必要在所建模型中考虑连续的和实际的纱线状态。

对于材料力学性能的理论分析模型，主要分为三种：层板理论，取向平均模型和有限元分析方法等。虽然这些方法在对力学性能预测上都有较好的贡献，但这些方法都是建立在对材料单胞尺度上来进行的研究，且所建立的单胞都使用了理想化的细观结构，忽略了实际结构的影响，所以要能更加精确地预测材料性能，更好地指导材料的可设计性，还需要进一步的努力，建立更精细的理论模型。

[1] A.P.Mouritz,M.K.Bannister,et al.Review of application for advanced three-dimensional fiber Textile composites[J].Composites:Part A,1999,(30):1445—1447.

[2] Alexander E,Bogdanovich.Advancement in manufacturing and application of 3-D woven preforms and composites[A].In:16thInternational conference on composites materials:Vol[C],Japan,2007:1—10.

[3] M K Bannister.Development and application of advanced texlile composites[N].Special Issue Paper,2004—4—22.

[4] 余育苗,王肖钧,王志海,李永池.三维正交机织复合材料的力学性能研究[J].实验力学,2008,23(3):206—209.

[5] Chen X,LW Taylor,LJ Tsai.An overnew on fabrication of three-dimensional woven textile preforms for composites[J].Textile Research Journal,2011,81(9); 932—944.

[6] Kadir,Bilisik.Multiaxis 3D woven preform and Properties of Multiaxis 3D woven and 3D orthogonal woven carbon/epoxy composites[J].Journal of Reinforced Plastics and Composites,2010,29:1173—1185.

[7] Mohamed M.H.,Bogdanovich A.E.,et al.A New Generation of 3D Woven Fabric Preforms and Composites[J].SAMPE Journal，2001,37(3):8—17.

[8] Liyong Tong,Adrian P.Mouritz,Michael K.Bannister.3D Fibre Reinforced Polymer Composites[M].Elsevier’s Composites and Ceramics,2002.

[9] 易洪雷,丁 辛.三维机织复合材料力学性能研究进展[J].力学进展,2001,31(2):162—165.

[10] Peirce F T.The geometry of cloth structure[J].Journal of the Textile Institute,1937,28(3):45—96.

[11] Love L.Graphical relationships in cloth geometry for plain,twill and sateen weaves[J].Textile Research Journal,1954,24(12):1073—1083.

[12] Dickson J.Practical loom experience on weavability limits[J].Textile Research Journal,1954,24(12):1083—1093.

[13] Kemp A.An extension of Peirce’s cloth geometry to the treatment of no-circular threads[J].Journal of the Textile Institute,1958,49(4):44—48.

[14] 罗查诺夫，库吉波夫，茹比科娃等著.徐子辛译.织物构造与设计(上册)[M].北京:纺织工业出版社，1955.

[15] 道德馄，吴以心，李兴国编.立体织物与复合材料[M].上海,中国纺织大学出版,1998.

[16] Byun J H,Chou T W.Elastic properties of three-dimensional angle-interlock fabric Preforms[J].Journal of the Textile Institute,1990,81(4):538—548.

[17] Ishikawa T,Matsushima M,Banaksu K,Watanabe N,Sunakawa M.Experimental results of interlaminar fracture toughness and in-plane strength of 3-D woven carbon/epoxy plates[A].In:Proc of seminar of the Japan society for composite materials:Vol[C],Tokyo,Japan,1996：51—52.

[18] Gu P.Analysis of 3D woven preforms and their composite properties [D].Raleigh:North Carolina State University,1994:89—97.

[19] Lee B,Herszberg I,Bannister M K,et al.The effect of weft binder length on the architecture of multilayer woven carbon performs[A].In:Scott M L,ed.Proceeding of the 11th International Conference on Composite Materials:Vol[C].Gold Coast:University of Melbourne,Australia,1997:260—269.

[20] 吴华利.三维正交机织复合材料结构和力学性能研究[D].武汉：武汉理工大学,2007.

[21] 郭兴峰.纬纱接结的三维正交机织物结构[J].纺织学报,2008,29(1):62—65.

[22] Xuesen Zeng,Louise P.Brown,et al.Geometrical modelling of 3D woven reinforcements for polymer composites:Prediction of fabric permeability and composite mechanical properties[J].Composites:Part A,2014,(56):150—160.

[23] Leong K H,Lee B,Herszberg I,et al.The effect of binder path on the tensile properties and failure of multilayer woven CFRP composites[J].Composites Science a Technology，2000,60(1):149—156.

[24] Hage CEI,Younes R,Aboura Z,Benzeggagh ML,Zoaeter M.Analytical and numerical modeling of mechanical properties of orthogonal 3D CFRP[J].Composites Science Technology,2009，(69):111—126.

[25] Cox BN,Dadkhah MS.The macroscopic elasticity of 3D woven composites[J].J Compos Mater，1995,29(6):785—819.

[26] Buchanan S,Grigorash A,Archer E,McIlhagger A.Analytical elastic stiffness model for 3D orthogonal interlock composites[J].Composites Science and Technology,2010,(70):1597—1604.

[27] Huang D,Abdi F.Analytical characterization and damage progression of three dimensional composites[J].AIAA.2006:1-19.

[28] Tan P,L Tong,GP Steven.Modeling approaches for 3D orthogonal woven composites[J].Journal of Reinforced Plastics and Composites,1998,17(6):545—577.

[29] Kim SJ,Ji KH,Paik SH.Numerical simulation of mechanical behavior of composite structures by supercomputing technology[J].Adv Compos Mater,2008,(17):373—407.

[30] Lee CS,Chung SW,Shin H,Kim SJ.Virtual material characterization of 3D orthogonal woven composite materials by large-scale computing[J].J Compos mater,2005,(39):851—863.

Development of Mechanical Model of 3D Orthogonal Woven Composites

JingYunjuan

(Tianjin Polytechnic University,Tianjin 300160,China)

Mesoscopic structure and theoretical models were reviewed,and the three dimensional orthogonal woven composites model were introduced in this paper.Some references were provided of the future research work.

3D orthogonal composites;mesostructure;theoretical model to the future research work

2014-09-12

荆云娟(1989—)，女，山西运城人，硕士研究生。

TS102.2

A

1009-3028(2014)06-0045-05