分形理论及其在绵阳市地质灾害研究中的应用★

卢 江 董宏戈 王 哲 李家明

(1.四川省地质矿产勘查开发局108地质队，四川 崇州 611230； 2.四川省地质矿产勘查开发局909地质队，四川 绵阳 621000；3.西南科技大学，四川 绵阳 621000； 4.四川正基岩土工程有限公司，四川 绵阳 621000)

分形理论及其在绵阳市地质灾害研究中的应用★

卢 江1董宏戈2王 哲3*李家明4

(1.四川省地质矿产勘查开发局108地质队，四川 崇州 611230； 2.四川省地质矿产勘查开发局909地质队，四川 绵阳 621000；3.西南科技大学，四川 绵阳 621000； 4.四川正基岩土工程有限公司，四川 绵阳 621000)

在介绍分形、分维涵义和分维测定方法以及分维在地学领域研究的方法的基础上，以绵阳市地质灾害空间分布为依据，采用网格等分加密覆盖法对绵阳市地质灾害系统进行了初步分析，得出了绵阳市地质灾害空间分布的分维值为0.893 9。

分形，分维，地质灾害，网络覆盖法

0 引言

分形理论(fractal theory)是一门新兴边缘学科，是由美籍法国学者曼德布罗特20世纪70年代中期建立的分形几何学[1，2]。他使人们对自然界中复杂现象的数学描述发生了革命性的变化，提出了定量描述自然界中不规则、复杂现象的强有力工具。因此，分形(fractal)与分维(fractal dimension)广泛应用于众多领域[3]。

1 分形与分维的涵义

1.1 分形的定义

所谓分形(fractal)，就是自然界中没有特征长度(即无标度)，不规则、无限复杂的不可微分的几何形体、构造以及现象的总称，其内部存在着自相似性或自仿射，即局部与整体相似。

1.2 分维的概念

分维(fractal dimension)是分形几何学定量描述分形集合特征和几何复杂程度的参数，其分维值不一定是整数，故称其为分数维，又叫分形维数。

欧氏几何中的空间是3维的，平面是2维的，直线是1维的，点是0维的，而在研究分形集的几何性质时，传统的“长度”“面积”“体积”的概念已经不够用了。在分形几何学中主要采用了“分数维”的计算方法。所谓“分数维”是指在更深、更广泛的意义上定义n维空间中超越了“长度、面积、体积”旧概念的新度量。它度量的是一个分形集“充满空间的程度”。例如，一个线团的维数，与观察方法有关，远看，它是一个点，是0维；近些看像球，有空间3维感；再近看，就看到了绳子，又成为1维的了；又如，一个分形集图案的分数维为1.6，是指它在空间的分布比1维空间复杂一些，而比2维空间简单一些。在欧氏空间中，把空间看成3维的，平面或球面看成2维，而把直线或曲线看成1维。引发人们注意到几何中也具有“相对关系”，以及维数的多样性。Benoit B. Mandelbrot“越过”传统几何学中的维数只能是整数0，1，2，3…的“传统整数维”(同时也超越了传统观念)，进入了看起来像是不可能的“分数维数”，分维出现了，它可以是任意正实数。

由于分形集的复杂性及其广泛应用性，因而对于不同的分形集需要用不同的测量方法，这导致了分形维数有多种定义，最有代表性的是Hausdorff维数和Box维数。

1)Hausdorff维数。对于任何一个有确定维数的几何体，若用与它相同维数的尺度r去度量，则可得到一确定的数值N；若用低于它维数的尺度r去量它,结果为无穷大；若用高于它维数的尺度r去量它，结果为0。其数学表达式为：N(r)∝r-Dh。上式两边取自然对数，整理后可得：

其中的Dh就称为Hausdorff维数，它可以是整数，也可以是分数。

Hausdorff维数是众多分维数中最重要的一个，它对一般的集合都有定义，在理论上意义重大。但是，在很多情形下很难计算或估计它的值，应用它来描述自然界复杂形态的几何特征，几乎是不可能的。实际中常用的分维数是Box维数。

2)Box维数。假设A是Rn上任意非空的有界子集，用尺度为r的n维盒Nr(A)是直径最大为r可以覆盖A的最少个数，则集合A的Box维数N(A)定义为:

1.3 分形维数的测量

由于分形维数的定义有很多，故计算分数维的方法也很多，不同的人采用不同的计算方法所得到的计算结果可能是不同的。总的要求是：分数维必须能够反映“在不断缩小直径的很小的比例下，去观测一个分形集，找出这个集的一个代表维数”，使它能够反映出图形的复杂程度，或“不规则程度的量度”，或“充满空间的程度”。测定分形维数的方法主要有以下几种[4]：

1)改变观察尺度求维数：用具有特征长度的基本图形去近似分形图形。

2)根据测度关系求维数：利用分形具有非整数维数的测度来定义维数。

3)根据相关函数求维数：C(r)∝r-a，幂指数a与分形维数D的关系:a=d-D，其中，d为欧氏空间维数。

5)根据频谱求维数：从频率的观点来看，所谓改变观察的尺度就是改变截止的频率。此处的截止频率是把较此更细小的震动成分舍去的界限频率。因此，如果某变动是分形，那么变换截止频率，不会改变频谱的形状。

1.4 分形理论在地学领域中的研究方法

在地球科学的研究工作中一般有三种分维的定义[5]，分别是：

1)容量维(Dk)。一般来说，如果已知某个分形体的自相似比，就可以采用Hausdorff维数的计算方法计算其维数。但是大自然中存在大量的在统计意义下的自相似体，它们的自相似比往往并不知道。这时采用上面的Hausdorff维数方法来计算其分形维数就比较困难了，为了解决这个问题，人们发展了一种计算容量的分维计算方法，即：

若N(d)是能覆盖住一个点集的直径为d的小球的最小数目，则该点集的容量维为：

2)信息维(Di)。设pi(d)为研究对象落在第i个球中的概率，其定义：

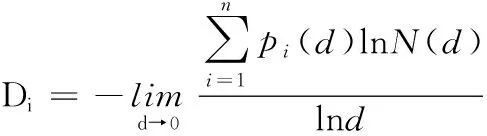
若概率分布均匀，则pi(d)=1/N，Di=Dk，多数情况下，Di≤Dk，可见信息维是容量的一种推广。

3)相似维(Ds)。对于某一具有相似的研究对象，若其可以分为N个单元，且每一单元相似比r与整体相似，其定义：

Ds=-lnN(r)/ln(r)。

本文主要是结合容量维和相似维两种方法，选用网格等分加密覆盖的手段进行分形分维分析。

2 分形理论在地质灾害系统研究中的应用

2.1 地质灾害系统及分形分维特征

地质灾害一般不是孤立的，而是与外界环境相互关联、相互作用的，彼此交织在一起构成了复杂的地质灾害系统。这个系统具有开放性、非线性和复杂性的特点。因此，对地质灾害系统的评价就难以运用定量化的方法加以研究。然而分形理论的提出和引入，就为地质灾害系统的定量化研究提供了新方法和新思路。

正是由于地质灾害系统具有分形分维特征，而地质灾害系统内各个子系统之间的相互作用和影响结果的宏观表现就是在某地某处发生地质灾害或出现地质灾害隐患点。因此本文力图从分形理论入手，研究绵阳市地质灾害系统的复杂程度。

2.2 地质环境条件背景及其地质灾害现状

绵阳市处于四川盆地西北部，介于盆地向丘陵、山地的过渡地带，研究区内地质构造复杂且地层岩性变化较大，进而导致岩体破碎。目前，区内已查明的灾害类型有滑坡、崩塌、泥石流、潜在不稳定斜坡及地面塌陷等地质灾害，其中滑坡275处，崩塌59处，泥石流55处，潜在不稳定斜坡13处和地面塌陷2处，共计灾害点404处[6]。

2.3 基于分形理论的绵阳市地质灾害系统研究

将绵阳市所有的地质灾害点以点的形式展布在地形图上，运用GIS的网格剖分功能将研究区分成若干个边长为r的正方形格子，计算出有灾害点落入的格子数N(r)，然后按照1/2的倍数缩小r值，并数出相应的格子数N(r)，拟合出一条直线，即：lnN(r)=a+blnr。

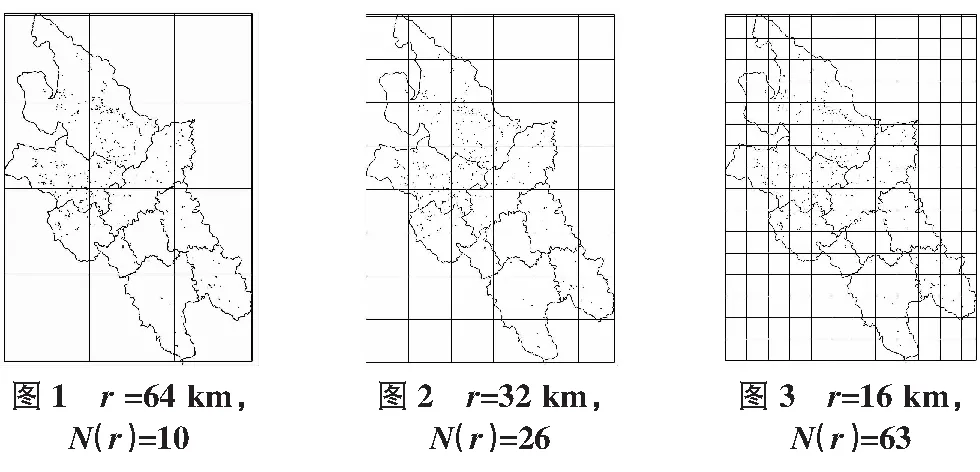
r分别取64 km,32 km,16 km,8 km,4 km,2 km,1 km,0.5 km，于是N(r)分别为10个,26个,63个,147个,267个,406个,548个,794个(见图1～图6。由于r=1和r=0.5时的网格太密，影响了图件的阅读效果，故文中未插入)。

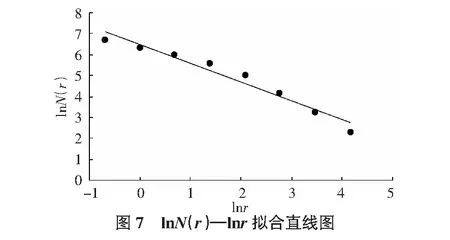
绘制lnN(r)—lnr双对数图(见图7)，并拟合直线：lnN(r)=6.458-0.893 9lnr，其相关系数为0.956 7。

由上述关系式可以看出，绵阳市地质灾害点空间分布的分维值D=0.893 9，介于0和1之间说明绵阳市地质灾害具有空间分维的特征，且分维值较大，反映了绵阳市地质灾害系统较复杂。作为表征研究对象几何复杂程度和几何分布关系的参数，分形理论的提出具有重要的研究意义，既解决了用整数维无法对地质灾害系统进行定量描述的瓶颈，又为分析地质灾害系统间的关系提供了研究手段，也为数值模拟提供了依据。同时，我们也应该意识到地质灾害系统的复杂性、数据的多样性和海量性等的特点，单纯依靠传统手段和数学方法进行地质灾害区划研究已经不能满足处理海量数据和生产实践的要求，应充分利用计算机技术和现代信息技术，特别是借助3S技术与分形理论的交叉融合，通过利用RS和GPS的数据收集提取等功能来实时地获得研究区域的地质环境和地质灾害现状等资料，借助于GIS的数据存储技术和专家系统对数据信息进行数据挖掘、融合和处理分析功能，对地质灾害系统的分维值的变化作出分析，并对地质灾害的发生、发展和演化规律作出预测。

[1] Mandelbrot B B.The Fractal Geometry of Nature[M].SanFrancisco:Freeman，1983.

[2] Mandelbrot B B.Fractal:Fom,Chance and Dimensions[M].SanFrancisco:Freeman，1977.

[3] 辛厚文.分形理论及其应用[M].北京:中国科学技术大学出版社,1993.

[4] 张济忠.分形[M].北京:清华大学出版社,1995：57-73.

[5] 夏玉成,陈练武,薛喜成.地学信息数字技术概论[M].西安：西安科技学院出版社,1999.

[6] 四川省地质工程集团公司.四川省绵阳市地质灾害调查与区划报告[R].2005.

Fractal theory and applications of geological hazards research in Mianyang city★

LU Jiang1DONG Hong-ge2WANG Zhe3*LI Jia-ming4

(1.SichuanBureauofGeologyandMineralResourcesof108GeologicalBrigade,Chongzhou611230,China;2.SichuanBureauofGeologyandMineralResourcesof909GeologicalBrigade,Mianyang621000,China;3.SouthwestUniversityofScienceandTechnology，Mianyang621000,China;4.SichuanZhengjiGeotechnicalEngineeringCo.,Ltd,Mianyang621000,China)

The paper introduces the concept of fractal and fractal dimension, the calculation of fractal dimension, the methodology and fractal theory of research method in geoscience. The paper preliminarily analyses hazards system research of Mianyang city on a foundation of the reference spatial distribution of geological hazards and gridding methods, then draws fractal dimension which is 0.893 9.

fractal， fractal dimension， geological hazards， gridding methods

1009-6825(2014)34-0066-03

2014-09-20★：科技部支撑计划项目“龙门山地震带小流域滑坡泥石流灾害监测预警技术研究与示范”(项目编号：2011BAK12B02)；国家自然科学基金项目(项目编号：41402248)；四川省教育厅科技创新团队项目(项目编号：12zd1106)；四川省非金属复合与功能材料重点实验室开放基金(项目编号：11zxfk06)

卢 江(1971- )，男，工程师； 董宏戈(1981- )，男，工程师； 李家明(1981- )，男，工程师

王 哲(1979- )，男，博士，讲师；

P694

A