深埋隧道突水多场信息演化规律分析

隋 来 才

(山西省交通科学研究院，山西 太原 030006)

深埋隧道突水多场信息演化规律分析

隋 来 才

(山西省交通科学研究院，山西 太原 030006)

以耿家山隧道为工程依托，通过数值模拟的方法演化深埋隧道突水前兆多场信息的变化规律，采取了针对性的隧道突水的防范措施，从而保障了隧道的顺利施工和人员的安全。

深埋隧道，突水，多场信息，数值模拟

0 引言

随着我国国民经济的快速稳定的发展，国家在交通基础设施方面的投资力度进一步加大，大量隧道频繁地出现在公路、铁路等工程建设中。然而隧道在施工过程中经常会出现突水的问题，这不仅会延误施工进度，造成不必要的财产损失，突水情况严重时还可能导致隧道塌方，威胁施工人员的生命安全。因此，为了保障隧道的顺利施工和人员的安全，研究隧道突水是十分必要的。国内外许多学者对隧道突水做了大量的研究，并得到了相应的科研成果。Stallman(1965)[1]利用数值方法演化了承压水的变化过程，得出了承压水随渗透系数变化的规律；Barton(1985)[2]对多场耦合作用下隧道突水过程进行了研究，得出了隧道突水过程中围岩应力和位移的变化规律；近年来，我国学者致力于隧道突水的研究，并取得了较为显著的成果。仵彦卿(1999)[3]提出了多场耦合作用下地下水的等效连续介质模型和裂隙网格介质模型；黄涛、杨立中(1999)[4]在考虑多场耦合作用下分析了围岩裂隙度对隧道突水量的影响规律，并建立数学模型对隧道的突水量进行了预测；王建秀(2001)[5]演化了隧道施工阶段岩溶蓄水构造对突水的影响过程，并提出了岩溶地区隧道施工的防水措施；刘高(2002)[6]研究了围岩破碎带和断层构造对岩溶地区深埋隧道涌突水的影响规律；刘斌(2010)[7]对隧道含水构造的水量进行了研究，从理论上系统地分析了含水地质构造对隧道突水的影响。

1 工程背景

耿家庄隧道位于霍州市白龙镇陈家庄村，设计为左右线分离式，两洞中轴线间距30 m。左线洞体全长967.0 m，进口段里程桩号为ZK14+898，洞口底板设计高程为682.879 m。

出口段里程桩号为ZK15+865，洞口底板设计高程为692.210 m；洞体最大埋深102.140 m，位于ZK15+546。右线洞体全长920.0 m，进口段里程桩号为K14+911，洞口底板设计高程为683.131 m；出口段里程桩号为K15+831，洞口底板设计高程为691.983 m；洞体最大埋深101.098 m，位于K15+556；隧道总体走向呈东西向为81°。

隧址区地层岩性结构较为简单，主要为二叠系下统下石盒子组(P1x)砂岩、泥岩互层；二叠系下统山西组(P1s)砂岩、泥岩互层；各层厚度约3.0 m～6.5 m，岩层较破碎，岩芯一般呈短柱状或饼状，底部砂岩较完整，呈长柱状。上覆第四系褐黄色硬塑粉质粘土及稍密粉土。隧道洞身围岩多为二叠系山西组强风化～中风化砂岩及泥岩，地层岩性较破碎，施工时极易造成小规模塌方。整体而言，隧道工程地质构造较为单一，不存在断层，但围岩岩层破碎；工程地质条件一般。

隧址区地下水类型主要有松散层孔隙水及奥陶系岩溶裂隙水。上层滞水富水性良好，且与隧道有水力联系，需考虑其对隧道的影响。根据区域资料，奥灰水水位标高660 m左右，而两隧道最低设计标高为977.42 m，水位远低于隧道设计标高，故岩溶水不会对该两隧道产生影响。

2 隧道突水过程多场信息演化规律分析

2.1 计算模型的建立

根据耿家庄隧道的地质情况建立计算模型，模型的尺寸为200 m(长)×100 m(宽)×100 m(高)，隧道为分离式深埋隧道，如图1所示，隧道各地层的力学、水力学参数如表1所示，取隧道的底板标高为685 m，隧道直径为9 m，衬砌200 mm，隧道顶部中间位置存在两处充满水的空腔，地表水在土体的渗透作用下汇集到含水空腔内，对腔体的四周和底面施加面压力代替空腔内水压力的作用，同时在空腔单元节点上施加节点水头在计算过程中模拟水的渗流作用。边界条件取限制数值模型ux，uy两个方向的位移和砂岩层底部uz方向的位移，含水空腔底面的节点水头为18 m，采用摩尔库仑准则进行流固耦合计算，来模拟隧道施工过程中关键点的应力、位移、渗流场的变化。开挖方式为全断面开挖，开挖步距为10 m，共20步，累计开挖长度为200 m，根据开挖步骤钝化已经开挖的土体，以研究随着隧道的开挖渗流稳态的变化规律。

为演化该分离式深埋隧道突水过程多场信息的变化规律，在隧道与含水空腔临近的土体周围设置防突层关键点实时监测应力、位移、渗流的多场信息，从而得到突水过程的演化规律，关键点设置如图2所示。

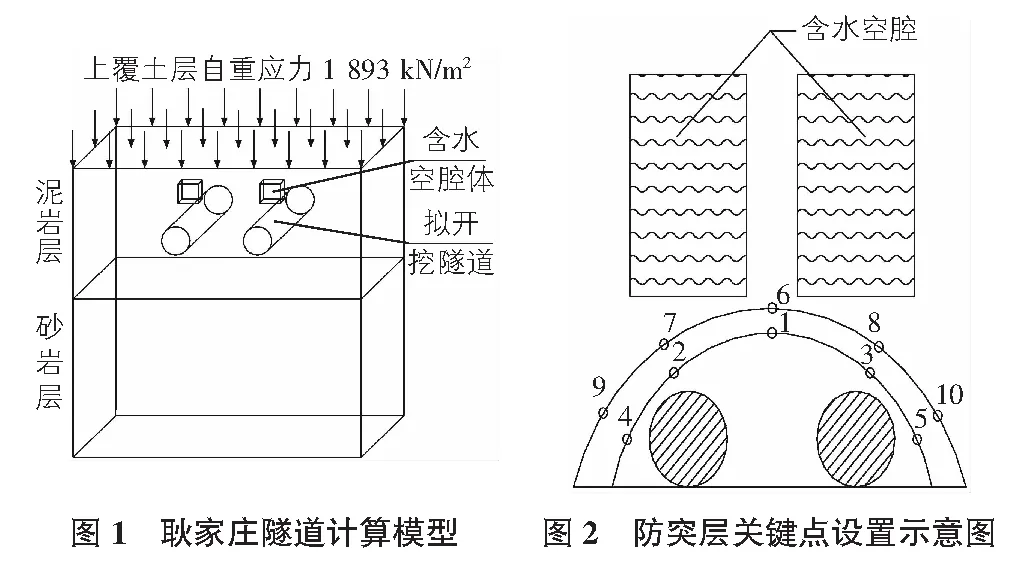
表1 数值模型岩石力学参数

岩性密度kN/m3弹性模量kN/m2泊松比μ粘聚力ckN/m2摩擦角ϕ/(°)应力参数K0渗透系数Km/sec泥岩0.22210000.2212280.640.0176砂岩0.27600000.2616360.750.0084

2.2 突水过程多场信息演化

2.2.1 渗流速度演化规律

从图3，图4中可以看出，渗流速度在含水空腔底部达到最大，且距离含水空腔越远渗流速度越小，z向渗流速度在两个含水空腔之间达到最大。从图5中可以看出，隧道未开挖时最大渗流速度为6.2×10-2m/s，z向渗流速度为2.35×10-2m/s；在隧道开挖至50 m时，含水空腔底部的最大渗流速度降低到5.53×10-2m/s，z向渗流速度也降低到2.01×10-2m/s；当开挖至100 m时，即含水空腔正下方时，最大渗流速度继续下降到3.73×10-2m/s，z向渗流速度降低到1.4×10-2m/s；当开挖至150 m时，此时掌子面已经远离含水空腔，底部最大渗流速度降低到3.4×10-2m/s，z向渗流速度降低到1.21×10-2m/s。当开挖至200 m时，底部最大渗流速度降低到3.3×10-2m/s，z向渗流速度降低到1.5×10-2m/s。从图5中可以看出，渗流速度总体趋势为随着开挖步而持续降低，当开挖接近含水空腔附件位置时，渗流速度降低速率变快，随着隧道掌子面逐渐远离含水空腔，渗流速度减小幅度变缓达到一个稳定值。

2.2.2 孔隙水压力演化规律

从图6中可以看出，土体中孔隙水压力呈阶梯式分布，随着地面标高的降低，孔隙水压力逐渐降低。从图7中可以看出，在隧道未开挖时，隧道防突层关键点6周围土体的初始孔隙水压力约为17.42 kN/m2；在隧道开挖至50 m时，关键点6周围土体孔隙水压力降低至16.85 kN/m2；在隧道开挖至100 m时，孔隙水压力小幅增大至16.87 kN/m2；当开挖至150 m时，孔隙水压力回落至16.85 kN/m2；当开挖至200 m时，孔隙水压力依旧稳定在16.85 kN/m2。从整体上看，在隧道开挖过程中，孔隙水压力开始小幅下降，随着开挖的推进逐渐趋于稳定。

2.2.3 应力场演化规律

从图8中可以看出，土体中z向应力大体呈阶梯式分布，随着地面标高的降低，z向应力逐渐增大。从图9中可以看出，在隧道未开挖时，隧道防突层关键点6周围土体的最大z向应力约为1 097.8 kN/m2；在隧道开挖至50 m时，z向应力增大至1 235.8 kN/m2；在隧道开挖至100 m时，z向应力继续增大至2 115 kN/m2且增大的速率变快；当开挖至150 m时，z向应力继续增大至2 580.6 kN/m2但增大的速率逐渐放缓；当开挖至200 m时，z向应力增大至2 610 kN/m2，此时围岩应力基本达到了自稳状态。整体上看，z向应力随着开挖步的增大而增大，开挖至含水腔下方时，应力增率迅速变大，边墙部位可能出现由于衬砌应力达到极限状态而出现突水或涌水现象。

2.2.4 位移场演化规律

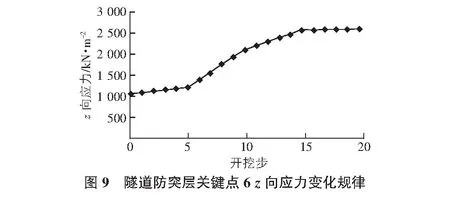
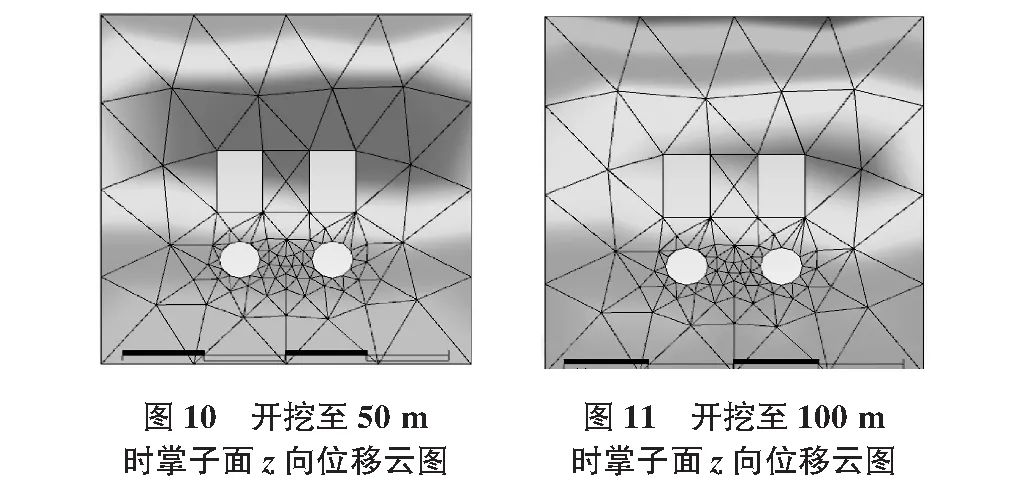
从图10～图12中可以看出，在隧道开挖至50 m时，z向位移为1.89 mm；在隧道开挖至100 m时，z向位移增大至3.96 mm；当开挖至150 m时，z向位移继续增大至8.3 mm且增大的速率明显加快；当开挖至200 m时，z向应力增大至9.86 mm且增大的速率放缓。从图13可以看出，z向位移随着开挖步的增大而增大，开始时增大速率较小，当开挖通过含水腔下方时，位移增率迅速变大，之后趋于平缓逐渐达到一个稳定的状态。

3 结语

本文以耿家庄隧道为依托工程，通过MIDAS GTS岩土工程数值模拟软件对隧道防突层区域渗流场、应力场、位移场信息随隧道开挖的变化进行了数值模拟，得到了隧道突水前兆信息演化规律，各场信息变化规律如下所述：

1)渗流速度总体趋势为随着开挖步而持续降低，当开挖接近含水空腔附件位置时，渗流速度降低速率变快，随着隧道掌子面逐渐远离含水空腔，渗流速度减小幅度变缓达到一个稳定值。

2)土体中孔隙水压力呈阶梯式分布，随着地面标高的降低，孔隙水压力逐渐降低。在隧道开挖过程中，孔隙水压力开始小幅下降，随着开挖的推进逐渐趋于稳定。整体上看，孔隙水压力的变化不大，可以基本认为是稳定的。

3)土体中z向应力大体呈阶梯式分布，随着地面标高的降低，z向应力逐渐增大。整体上看，z向应力随着开挖步的增大而增大，开挖至含水腔下方时，应力增率迅速变大，边墙部位可能出现由于衬砌应力达到极限状态而出现突水或涌水现象。

4)z向位移随着开挖步的增大而增大，开始时增大速率较小，当开挖通过含水腔下方时，位移增率迅速变大，之后趋于平缓逐渐达到一个稳定的状态。

[1] Stallman R W.Steady one-dimensional fluid flow in a semi-infinite porous medium with sinusoidal surface temperature[J].Journal of Geophysical Research,1965,70(12):2821-2827.

[2] Barton N,Bandis S,Bakhtar K.Strength,deformation and conductivity coupling of rock joints[A].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon[C].1985:121-140.

[3] 仵彦卿.地下水与地质灾害[J].地下空间,1999,19(4):303-310.

[4] 黄 涛,杨立中.渗流与应力耦合环境下裂隙围岩隧道突水量的预测研究[J].铁道学报,1999,21(6):75-80.

[5] 王建秀,何 静.大型地下工程岩溶涌(突)水模式的水文地质分析及其工程应用[J].水文地质工程地质,2001,28(4):49-52.

[6] 刘 高,杨重存.深埋长大隧道涌(突)水条件及影响因素分析[J].天津城市建设学院学报,2002,8(3):160-164.

[7] 刘 斌.基于电阻率法与激电法的隧道含水地质构造超前探测与突水灾害实时监测研究[D].济南:山东大学,2010.

Analysis of water inrush evolution in deep-buried tunnel under the multi-field information

SUI Lai-cai

(ShanxiTransportationResearchInstitute,Taiyuan030006，China)

In this paper,based on Gengjiashan tunnel engineering, the law of water inrush evolution in deep-buried tunnel under the multi-field information is showed by numerical simulation and measures are taken to prevent water inrush, which ensure tunnel smooth construction and personnel safety.

deep-buried tunnel, water inrush, multi-field information, numerical simulation

1009-6825(2014)34-0177-03

2014-09-26

隋来才(1982- )，男，工程师

U456.32

A