浅谈结构周期比的调整

叶坚如

（上海亚新工程顾问有限公司，上海 200052）

《高层建筑混凝土结构技术规程》第3. 4. 5 条对周期比作出相应规定[1]。结构的扭转平动周期比是指在结构扭转为主的第一自振周期与平动为主的第一自振周期之比，A 级高度高层建筑不应大于0.9，B 级高度高层建筑、复杂高层建筑不应大于0.85。

控制周期比的目的是使结构抗侧力构件的平面布局更有效、更合理，使结构的扭转效应（相对于侧移）不至于过大，它体现的是结构抗侧刚度与抗扭刚度之间的相对关系，侧重的并非它的大小。简言之，周期比不是要求建筑物自身如何的结实，要求的是结构承载构件的布置更具合理性[2]，以保证结构在侧向力作用下不出现较大的扭转变形，特别是在罕遇地震情况下的扭转效应。

PKPM 设计软件未直接给出结构的周期比，其验算应选择刚性楼板假定，根据周期、地震作用与振型输出文件WZQ. OUT 中周期值自行判定第一扭转或平动周期。一般情况下，第一周期、第二周期均为平动周期，第三周期为第一扭转周期。《建筑抗震设计规范》第3.5.3 条第3 款提出“结构在两个主轴方向的动力特性宜相近”[3]，以使结构在两个主轴方向上具有比较相近的抗震性能。一般认为结构两个主轴方向第一平动周期相差不大于20%为相近。

1 工程概况

某一厂房高层框架结构，地下1 层，地上6 层，局部7 层，出地面建筑总高度为38.2 m，平面呈矩形，总长80 m，总宽48 m，柱距8 m×8 m。该工程位于上海市金山工业园区内，结构抗震基本设防裂度为7 度，设计基本地震加速度为0.1 g，设计地震分组为第一组，Ⅳ类场地，框架抗震等级为二级，属于A 级高度的高层建筑。该建筑平面对称，整个车间建筑形式为简洁的长方体，没有采用花哨的建筑形式，没有大跨度的出挑及弧线造型等，符合规范规定的建筑抗震概念设计。标准层结构平面布置如图1。

在结构方案初期，框架柱尺寸为900 mm×900 mm，框架梁尺寸主要为450 mm×800 mm，采用SATWE 软件计算，最初试算其前三个周期结果如表1。

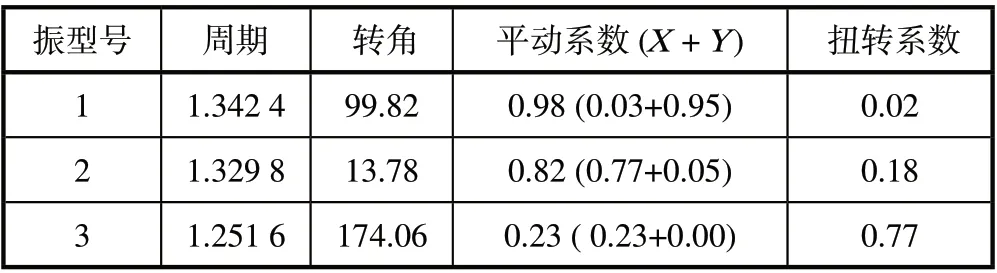
表1 最初试算结果

一般平动系数加上扭转系数等于1，所以，平动系数大于0.5 的振型，扭转周期就小于0.5，即该振型为平动振型；扭转系数大于0.5 的，为扭转振型。在平动系数大于0.5 的振型里，必然存在一个周期值最大的振型（一般就是振型1）即为第一平动周期。

从计算的结果显示，其第一平动周期T1应为振型号1，第一扭转周期Tt应为振型号3，第一扭转周期与第一平动周期之比为Tt/T1=1.251 6/1.342 4=0.932>0.9，不满足要求，因此，需要对原设计方案进行局部调整。

2 计算结果分析

在进行方案调整前，首先要做好分析工作，切忌盲目调整。只有查出问题关键所在，采取相应措施，才能有效解决问题。

图1 结构平面布置图

首先查看“结构整体空间振动图”，根据三维振型动画，可以一目了然地看出每个振型的型态，可以判断结构的薄弱方向，也可以看出结构计算模型是否存在明显的错误。

图2 为结构第一，二，三整体振动图，由第一振型可以看出整体模型是清晰地朝y 方向平动，第三振型整体模型是清晰地按中心进行扭动，而第二振型整体模型不是清晰地整体朝x 方向平动，而是很小地按中心进行扭动。这说明结构沿两个主轴方向的抗侧移刚度有相差，结构的抗扭刚度相对其中一主轴的抗侧移刚度是合理的，但相对于另一主轴的抗侧移刚度则偏小。为满足规范的要求周期比，应加强抗侧刚度小的主轴方向的刚度。

由材料力学中的圆轴扭转实验，我们不难得出抗侧力构件距离结构的刚度中心越远，其对结构的抗扭刚度贡献越大的结论。因此，当周期比不满足《高规》第3. 4. 5 规定的限值，通过加大结构外围刚度（增大外围刚度能够显著提高结构整体的抗扭刚度），减小结构内部刚度（能够减小结构整体的抗侧刚度，同时对结构整体的抗扭刚度削弱甚微），往往能够获得意想的结果。

3 设计方案的调整

根据这一思路，在模型调整过程中，为使第二平动周期加大，应调整抗侧力结构的布置，增大结构外围（主要是沿第一振型转角方向）刚度，即加大两端开间的抗侧刚度。首先考虑加大长度方向的两端（即图1 中的 1 轴和11 轴）的柱截面，框架柱尺寸由900 mm×900 mm 加大至900 mm×1 000 mm 后，经计算其前三个周期如表2。

从计算的结果显示，第一扭转周期与第一平动周期之比为Tt/T1=1.237 5/1.332 7=0.929>0.9，还是不满足要求。由计算结果可以看出，加大柱截面对抗扭刚度的提高有限，而且周期改变也不大。查看“结构整体空间振动图”，和没调整时的三维振型动画基本一致。即使把柱加大至900 mm×1 100 mm 后，计算结果仍然难以令人满意。

图2 结构整体振动图

因此，考虑加大框架樑截面。把长度方向的两端（即图1 中的1 轴和11 轴）沿全长范围内的框架樑加大，试着从450 mm×900 mm 开始，计算后，周期比还是不满足要求。但查看“结构整体空间振动图”，从第二振型可以看出整体模型是比较清晰地朝y 方向平动了。然后经过几次试算，框架樑尺寸从450 mm×1 000 mm直到用到450 mm×1 100 mm 时，计算得到其前三个周期如表3。

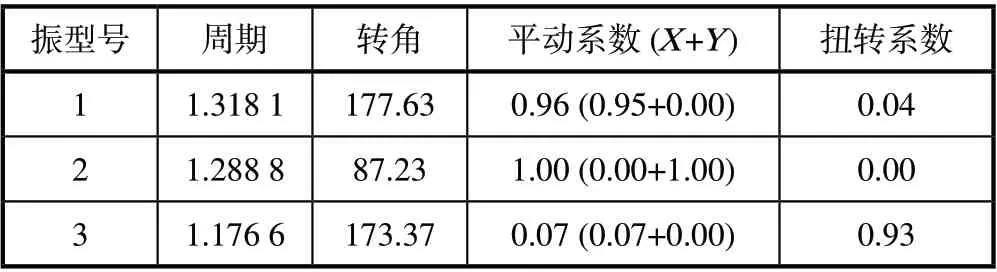
表3 框架樑调整计算结果

从计算的结果显示，第一扭转周期与第一平动周期之比为Tt/T1=1.176 6/1.318 1=0.893<0.9，满足要求。可见樑截面加大后，显著提高了结构的抗扭刚度，第二振型改为y 方向平动为主的振型，第一振型变为x方向平动为主的振型，而且周期比也有显著减小。可见，采取的措施有效提高了结构的抗扭刚度，结构的计算结果趋于合理。

在调整周期比的同时，原Y±5%偶然偏心的工况下楼层最大位移超限值也得到很大的改善。

4 结论

本文结合实际工程，对高层建筑结构扭转控制及调整的方法进行了探析，对于平面呈矩形框架结构，在“结构整体空间振动图”的帮助下进行调整。在调整中，如加大两端开间的柱截面效果不明显，可以考虑加大开间两端的框架樑，樑越高，周期比的计算越容易通过。希望能为相关人士提供一些参考性的建议。

[1] JGJ3-2010.高层建筑混凝土结构[S].中国建筑工业出版社，2010.

[2] 王翔宇.任力勇.谈高层结构设计中的常用电算指标[J].林业科技情报2006,(02) : 32-33

[3] GB50011-2010.建筑抗震设计规范[S].中国建筑工业出版社，2011.

[4] 中国建筑科学研究院PKPM CAD 工程部.多层及高层建筑结构空间有限元分析与设计软件(墙元模型)用户手册 2010 版.