一种线性走时插值射线追踪改进算法*

卢江波 方 志

(中国长沙410082湖南大学土木工程学院)

一种线性走时插值射线追踪改进算法*

(中国长沙410082湖南大学土木工程学院)

针对线性走时插值算法(LTI)不能正确追踪逆向传播射线的问题， 目前已提出多种改进算法， 如扩张收缩LTI算法、 循环计算LTI算法、 动态网络最短路径射线追踪算法等， 但这些算法的计算效率普遍偏低． 在分析各种改进LTI算法的优劣后， 本文提出了改进动态网络最短路径射线追踪算法. 该改进算法依据波的传播规律以及LTI算法的基本方程， 排除动态网络最短路径射线追踪算法中大量冗余节点计算, 并采用传统的二叉树堆排序算法对波前阵列节点进行管理． 数值算例表明， 本文提出的改进算法具有较高的计算效率， 其计算效率是动态网络最短路径射线追踪算法的4.5—30倍， 是原始LTI算法的2—6.5倍； 当动态网络最短路径射线追踪算法采用堆排序算法时， 改进算法的计算效率是其3.5—15倍．

射线追踪 线性走时插值 改进算法 波前扩展 计算效率

引言

射线追踪技术在地震层析成像以及混凝土超声波射线层析成像等领域具有重要作用. 目前常用的射线追踪方法主要有两点射线追踪算法(包括试射法)(Julian, Gubbins, 1977； 徐涛等, 2004； 田玥， 陈晓非， 2005)、 弯曲法(Thurber, Ellsworth, 1980; Xuetal, 2006, 2010)、 有限差分解程函方程法(Vidale, 1988; Qinetal, 1992; 李振春等， 2004)、 最短路径法(Moser, 1991; 赵爱华等, 2000； Zhaoetal, 2004; Baietal, 2010; 赵爱华， 徐涛， 2012)和LTI (linear travel-time interpolation)射线追踪算法(Asakawa, Kawanaka, 1993; 赵改善等， 1998; Cardarelli, Cerreto, 2002; 黄靓， 黄政宇, 2002; 聂建新， 杨慧珠, 2003; 张建中等, 2003, 2004; 黄靓， 2008； 张东等, 2009; 卢江波， 方志， 2014)等． 其中， LTI射线追踪算法因其计算精度较高、 计算速度较快， 且适用于任意复杂的速度介质模型， 在地震层析成像等领域得到广泛应用． 但原始LTI算法(Asakawa, Kawanaka, 1993)所采用的由震源向模型边界外推的计算方式， 不能正确追踪逆向传播的射线， 影响地震层析成像的精度．

针对这一问题， 不少研究人员提出了多种改进算法. 例如： 黄靓和黄政宇(2002)及黄靓(2008)提出了扩张收缩LTI算法， 卢江波和方志(2014)提出了扩张收缩LTI改进算法， 张东等(2009)提出了循环计算LTI算法； 此外， 张建中等(2003， 2004)将波前扩展方式与LTI基本方程相结合， 提出了动态网络最短路径射线追踪算法. 这些算法中， 扩张收缩LTI算法、 扩张收缩LTI改进算法以及循环计算LTI算法都需要迭代计算， 对于复杂的速度模型以及网格划分较为精细的模型， 其迭代次数较多， 计算效率偏低. 动态网络最短路径射线追踪算法能够一次计算出所有节点的走时， 具有相对较高的计算效率， 且也能有效解决上述问题， 但该算法在进行波前扩展时， 所选择的插值线段不够合理， 无效重复计算较多， 计算量大; 此外， 该算法采用快速排序法及插入排序法管理波前阵列节点， 效率较低．

本文针对动态网络最短路径射线追踪算法存在的不足对其进行改进. 首先依据波的传播规律以及LTI算法的基本方程， 选择更为合理的插值线段， 并排除该算法中的无效重复计算； 然后采用传统的二叉树堆排序算法对波前阵列节点进行管理， 以提高该算法的计算效率．

1 LTI算法的基本方程

如图1所示， 射线经单元下边界的AB节段到达C节点， 射线与AB的交点为D．A点及B点走时分别为tA和tB， 节段AB长为L， 单元慢度为s，C点距A点的水平及竖向距离均为已知， 分别为xC，yC． 建立以A点为原点的局部坐标系， 确定A，B，C，D点的局部坐标． 现推导C点走时以及交点D距A点长度r的计算公式(Asakawa, Kawanaka, 1993; 赵改善等， 1998)．

由线性追踪算法的基本假设可得D点的走时为

图1 经过边界AB到达C点的射线路径图Fig.1 The diagram of ray path from segment AB to C

(1)

根据D点的走时， 结合单元慢度以及各点的局部坐标等条件， 可得C点的走时为

(2)

将式(1)代入式(2)得

(3)

根据费马原理， tC对r的一阶偏导数应满足等于零的条件， 即(设Δt=tB-tA)

(4)

当L2s2-Δt2>0时， 解方程(4)可得

(5)

若r≥0且r≤L, 则

(6)

若r<0或r>L， 则计算r=0和r=L时的tC值， 并取两者较小值作为最终tC值．

当L2s2-Δt2≤0时， tC的计算方法与r<0或r>L时的情况相同．

2 LTI算法及动态网络最短路径射线追踪算法存在的不足及改进

图2 LTI算法存在的问题 Fig.2 Problems of LTI algorithm

对于这一问题， 张建中等(2003， 2004)提出的动态网络最短路径射线追踪算法能予以有效解决. 但是该算法在进行波前扩展时， 选择的插值线段不够合理， 无效重复计算较多． 现以图3所示均质模型为例， 对该算法的基本步骤及其计算策略进行详细说明， 同时依据波的传播规律以及LTI算法的基本方程对该算法进行改进， 改进算法的基本步骤及其计算策略如图4所示. 具体步骤及改进分析如下:

1) 首先计算震源S所在单元中所有节点的走时， 如图3a及图4a所示， 然后将这些节点加入波前阵列中用于下一步计算．

2) 从波前阵列中找出走时最小的节点作为当前扩展点， 假定节点为A1， 然后对A1的所有邻点(S，A2，A12)一一进行分析， 如图3b--d及图4b--d所示， 并根据邻点的不同状态采用不同的计算策略， 具体如下：

① 邻点未计算过的策略. 当前扩展点不与该邻点形成插值段， 而是以当前扩展点为震源， 对单元内还未做过扩展点的节点进行计算． 对邻点A12进行分析时， 即采用这一策略， 如图3b所示． 事实上， 对于邻点未计算过的情况， 只需利用当前扩展点A1的走时信息对该邻点进行计算(图4b). 考虑波沿单元边界的速度与通过单元内部的速度不同， 将Ⅱ号单元中的节点分为A1A4、A1A14边界上的节点以及其它节点； 对于其它节点， 显然在A12做扩展点， 并与A1形成插值段时进行计算更为合理有效； 对于A1A4、A1A14边界上的节点， 与最短路径法的计算方法相同， 只需计算节点A2以及A12， 而节点A2的计算则可放在对邻点A2的分析中, 因此， 此时只需对节点A12进行计算．

② 邻点已计算过但未做过扩展点(不确定该邻点是否已得到理论最小走时)的策略. 当前扩展点与该邻点形成走时插值段， 并应用LTI基本方程计算插值段所在单元中还未做过扩展点的节点． 对邻点A2进行分析时， 即采用这一策略， 具体如图3c所示． 事实上， 对于邻点已计算过但未做过扩展点的情况， 只需利用当前扩展点A1的走时信息对该邻点进行计算(图4c). 由LTI基本方程式(3)可知， 在邻点A2计算过但未做过扩展点的情况下， 节点A1与A2形成插值段的意义不明确． 而且节点A2做扩展点时， 节点A2与A1也会形成插值段， 此时， 节点A1、A2均确定得到最小走时． 显然， 与未做过扩展点的邻点A2形成插值段既不合理也无必要． 但考虑节点A2的理论射线路径可能经过节点A1(如Ⅱ号单元的速度远大于Ⅰ号单元)， 因此， 在不形成插值段的情况下， 还需利用节点A1的走时信息对节点A2进行计算．

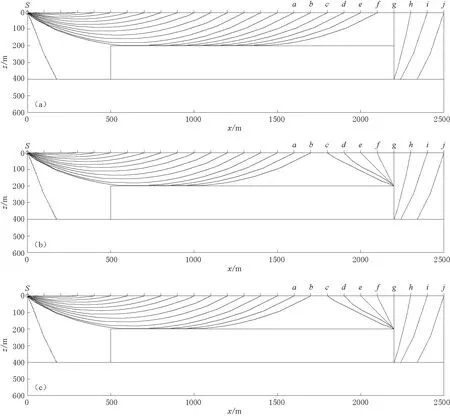
③ 邻点已做过扩展点(可以确定该邻点已得到理论最小走时)的策略. 当前扩展点与该邻点形成走时插值段， 并应用LTI基本方程计算插值段所在单元中还未做过扩展点的节点． 对邻点S进行分析时， 即采用这一策略， 具体如图3d所示． 实际上， 在当前扩展点与已做过扩展点的邻点形成插值段时， 并不需要对插值段所在单元中所有未做过扩展点的节点进行计算， 此时仅需考虑位于当前扩展点一侧且不与插值段在同一边界的节点(图4d). 而且在对这些节点进行计算时， 还可以通过规定节点的计算顺序， 并增加一些判断条件， 进一步排除无效重复计算. 具体为： 先计算位于插值段A1S对边A4A7， 且与当前扩展点A1处于同一位置的节点A4， 然后再依次计算其它节点A3、A2； 在节点计算前对节点进行判断， 以节点A4为例， 若节点已获得的走时小于当前扩展点邻点的走时与节点至当前扩展点的走时之和, 即tA4

a) 计算范围的确定. 首先， 对于与插值段处于同一边界的节点， 显然只需考虑与当前扩展点相邻的节点， 当邻点已做过扩展点时(如图3d中的节点S)， 不需要计算， 若邻点未做过扩展点， 则可按照上面的计算策略①或②进行计算， 此时无需考虑； 然后， 对位于邻点一侧且不与插值段处于同一边界的节点(A5—A9)， 可知在节点S已做过扩展点的情况下， 若A5—A9节点的理论射线路径过A1S插值段， 则交点必然为节点S． 现对节点S的左邻点A11进行分析， 若节点A11的理论最小走时小于或等于节点S的理论最小走时， 则节点A6—A9的理论射线路径不过A1S插值段， 因为这些节点通过A11计算得到的走时较通过A1S插值段更小； 若A11的理论最小走时大于节点S的理论最小走时(图3d)， 则当A11做扩展点时， 节点S必已做过扩展点，A11将与节点S形成插值段， 通过对A11一侧的节点进行计算， 节点A6—A9能得到最小走时. 无论哪种情况均不用利用A1S插值段对节点A6—A9进行计算． 对于节点A5， 可放在节点S做扩展点时进行计算， 考虑节点S做扩展点时， 节点A11和A1可能均未做过扩展点， 而节点A11和A1做扩展点时， 又只考虑位于节点A11或A1一侧的节点，A5将不能得到最小走时， 因此在节点S为当前扩展点、 而其邻点A11和A1均未做过扩展点的情况下， 除对节点A11和A1进行计算外， 还需增加节点A5的计算(具体见计算策略④)．

b) 节点计算前的判断条件. 以图4d中的节点A4为例进行说明. 显然， 邻点S的走时为插值段A1S上的最小走时， 节点A4到插值段A1S的最短距离为A1A4. 根据LTI基本方程式(1)和(2)可知， 若tA4

c) 节点计算后的判断条件. 假定A4满足费马原理的射线过当前扩展点A1. 显然， 节点A3和A2满足费马原理的射线也过当前扩展点A1. 如果A2—A4的理论射线路径过A1S插值段， 那么这些节点的理论射线路径必然沿A1A4边界传播， 与最短路径法的计算方法相同， 只需对A1的邻点A2进行计算即可. 而节点A2的计算则可放在对邻点A2的分析中. 因此， 当A4满足费马原理的射线过当前扩展点A1时，A4后面的节点A3和A2均不用计算．

以上分析针对的是当前扩展点为单元端节点的情况， 对于当前扩展点为中间节点的情况亦有同样的结论. 以节点A11为当前扩展点、S为其已做过扩展点的邻点为例， 节点的计算顺序从A6到A9， 若某节点满足费马原理的射线过当前扩展点A11， 假定为A6， 则根据LTI基本方程可以证明，A7—A9满足费马原理的射线也过当前扩展点A11． 如果A7—A9的理论射线路径过A11S插值段， 那么这些节点的理论射线路径必然过节点A11． 现对节点A11的左邻点A10进行分析. 如果节点A10的理论最小走时小于或等于节点A11的理论最小走时， 则节点A7—A9的理论射线路径必然不过A11S插值段， 因为这些节点通过A10计算得到的走时较通过A11计算的走时更小； 如果节点A10的理论最小走时大于节点A11的理论最小走时， 那么当节点A10做扩展点时， 节点A11必然已做过扩展点，A10与A11将形成插值段， 通过对A10一侧的节点进行计算，A7—A9可得到最小走时； 无论哪种情况，A6后面的节点A7—A9均不用计算．

④ 如果当前扩展点为单元的中间节点， 且其两个邻点均未做过扩展点， 则需利用当前扩展点的走时信息， 对位于当前扩展点对边， 且与当前扩展点处于同一位置的节点进行计算． 以图4d为例， 如果I号单元右边界上的中间节点A2为当前扩展点， 且其两个邻点A1及A3均未做过扩展点， 则需利用A2的走时信息对A9及A15进行计算． 需要特别说明的是， 这一条计算规则是改进算法特有的. 动态网络最短路径射线追踪算法没有这一规则．

对于以上4种计算策略， 所有节点在计算后， 都需进行如下处理： 若节点之前未被计算过， 则更新其走时并将其加入波前阵列中； 若节点之前已计算过， 而新计算出的走时小于原来的走时， 则更新其走时． 在分析完当前扩展点的所有邻点后， 将当前扩展点从波前阵列中删除．

3) 重复步骤2)， 直到模型中所有节点均做过扩展点， 此时所有节点均得到最小走时， 图3e、 图4e为最终状态．

对比图3与图4可以看出， 动态网络最短路径射线追踪算法存在较多的无效重复计算， 经改进后， 该算法的节点计算量明显减少． 此外， 动态网络最短路径射线追踪算法采用快速排序法和插入排序法管理波前阵列节点， 并认为这种排序方法要优于二叉树堆排序算法， 且两者的运行时间分别为O(n)和O(nlgn)， 式中n表示当前波前阵列的节点数(王辉， 常旭， 2000； 张建中等*张建中等(2003， 2004)在引用王辉和常旭(2000)一文时， 认为n为总节点数. 实际上是误解了原文的意思.， 2003， 2004). 但是， 这一结论的前提是波前阵列节点始终保持从小到大的排列顺序． 事实上， 采用堆排序算法对波前阵列进行管理并不要求波前阵列节点保持这种顺序， 而仅要求堆结构在插入、 更新以及删除节点后仍保持最小堆的性质即可， 整个过程的运行时间为O(nlgn)(Cormenetal, 2009)． 因此二叉树堆排序算法实际上要优于插入排序算法． 当然， 除二叉树堆排序算法外， 还存在性能更为优越的算法， 如Fibonacci堆、 quake堆以及Brodal队列等(Brodal, 2013)， 但这些算法较为复杂， 实用性还存在不足． 综合考虑， 本文仍采用传统的二叉树堆排序算法对波前阵列节点进行管理．

3 数值算例

为说明原始LTI算法存在的问题, 比较各算法的计算效率, 以及验证动态网络最短路径射线追踪算法和本文改进算法的有效性， 建立了如图5所示的存在高速区和低速区的连续介质模型， 其整体尺寸为2500 m×600 m. 其中深度在400—600 m之间的区域为高速区， 速度为6000 m/s； 深度在200—400 m之间且水平方向在500—2200 m的区域为低速区， 速度为500 m/s； 其余区域的速度随深度增加而线性增加， 深度z处的速度v(z)=v0(1+βz)， 式中v0取2000 m/s，β取0.001． 震源S位于模型的左上角， 接收点R均匀布设于模型上边界， 间距为100 m； 单元大小为5 m×5 m， 共有6×104个单元， 单元边界划分段数为1．

图5 模型速度Fig.5 Velocity model

图6 各接收点的理论射线路径Fig.6 Theoretical ray paths of all receiving points

图7 原始LTI算法(a)、 动态网络最短路径射线追踪算法(b)和本文改进算法(c)的射线追踪结果Fig.7 Ray path tracing results by the three algorithms(a) Original LTI algorithm; (b) The shortest path ray tracing algorithm with dynamic networks; (c) Improved algorithm presented in this study

图8 原始LTI算法(a)、 动态网络最短路径射线追踪算法(b)和本文改进算法(c)的走时相对误差a图中x<500 m的区域没有出现如b， c图所示的等高线， 是因为该区域内的相对误差所对应的颜色为浅色， 未能有效显示所致. 图9也存在类似的情况Fig.8 Travel time relative errors by three algorithms (a) Original LTI algorithm; (b) The shortest path ray tracing algorithm with dynamic networks; (c) Improved algorithm presented in this study. The reason why the contour in the x<500 m do not presentin Fig.8a like Figs.8b or 8c is that the color which corresponds to the value of relative error in thex<500 m was too light to present in Fig.8a. The similar situation is presented in Fig.9

图9 原始LTI算法(a)、 动态网络最短路径射线追踪算法(b)和改进算法(c)的走时绝对误差Fig.9 Travel time absolute error by three algorithms(a) Original LTI algorithm; (b) The shortest path ray tracing algorithm with dynamic networks; (c) Improved algorithm presented in this study

对比图7a与图6可以看出， 原始LTI算法对于大多数接收点均能正确追踪其射线路径， 但当接收点的理论射线路径存在逆向传播的射线时(如图6中的c，d，e，f点)， 原始LTI算法不能对其进行正确的射线追踪． 图7b, c中各接收点的射线路径与图6中的理论射线路径一致， 表明动态网络射线追踪算法和本文改进算法均能考虑逆向传播的射线， 能够正确处理复杂介质模型中接收点的射线追踪问题．

从图8和图9可以看出， 原始LTI算法在存在逆向传播射线的区域, 其走时相对误差和绝对误差较大， 最大分别达到43.36%和297.8 ms； 而动态网络最短路径射线追踪算法和本文改进算法则不存在这一问题， 均能够正确计算各节点的最小走时， 其最大相对误差和绝对误差分别为3.96%和1.5 ms．

为对比3种算法的计算效率， 以图5所示模型为计算对象， 单元边界划分段数为1， 2， 4， 10， 20和30等6种情况， 分别记录各算法的计算时间(不包括算法的前处理过程). 其中, 动态网络最短路径射线追踪算法采用插入排序法及二叉树堆排序法对波前节点进行管理， 本文改进算法只采用二叉树堆排序法． 计算机CPU主频为4.3 GHz， 对比结果如表1所示.

表1 3种算法计算效率的对比Table 1 Comparison of computational efficiency for three algorithms 单位： s

从表1可以看出， 本文改进算法具有较高的计算效率， 是动态网络最短路径射线追踪算法的4.5—30倍， 是原始LTI算法的2—6.5倍； 当动态网络最短路径射线追踪算法采用堆排序算法时， 本文改进算法的计算效率是其3.5—15倍．

图10 本文改进算法对Marmousi速度模型的初至波计算结果 (a) 初至波等时线; (b) 相对误差Fig.10 The first arrival calculations result based on Marmousi velocity model by using the improved algorithm presented in this study (a) Isochrons of first arrivals; (b) The relative error

4 讨论与结论

动态网络最短路径射线追踪算法能够有效解决原始LTI算法不能正确追踪逆向传播射线的问题， 且只需一次扩展计算就能得到所有节点的最小走时， 具有较高的计算效率. 但该算法存在较多的无效重复计算， 且其波前阵列节点的管理方法效率较低. 为此本文根据波的走时信息以及LTI基本方程提出了改进动态网络最短路径射线追踪算法， 排除了动态网络最短路径射线追踪算法中大量的节点计算， 同时采用传统二叉树堆排序法管理波前阵列节点， 较大幅度提高了该算法的计算效率. 数值算例表明， 本文提出的改进算法具有较高的计算效率， 是动态网络最短路径射线追踪算法的4.5—30倍， 是原始LTI算法的2—6.5倍； 当动态网络最短路径射线追踪算法采用堆排序算法时， 本文改进算法的计算效率是其3.5—15倍． 此外， 若将本文的改进算法用于三维模型， 则效果将更为显著.

黄靓， 黄政宇. 2002. 线性插值射线追踪的改进方法[J]. 湘潭大学自然科学学报， 24(4): 105--108.

Huang L, Huang Z Y. 2002. An improved method of linear interpolation ray tracing[J].NaturalScienceJournalofXiangtanUniversity, 24(4): 105--108 (in Chinese).

黄靓. 2008. 混凝土超声波层析成像的理论方法和试验研究[D]. 长沙: 湖南大学土木工程学院: 33--36.

Huang L. 2008.MethodologyandExperimentResearchonConcreteUltrasonicComputerizedTomography[D]. Changsha: College of Civil Engineering, Hunan University: 33--36 (in Chinese).

李振春， 刘玉莲， 张建磊， 马在田， 王华忠. 2004. 基于矩形网格的有限差分走时计算方法[J]. 地震学报， 26(6): 644--650.

Li Z C, Liu Y L, Zhang J L, Ma Z T, Wang H Z. 2004. Finite-difference calculation of traveltimes based on rectangular grid[J].ActaSeismologicaSinica, 26(6): 644--650 (in Chinese).

卢江波, 方志. 2014. 线性走时插值射线追踪算法的改进[J]. 湖南大学学报： 自然科学版, 41(1): 39--44.

Lu J B, Fang Z. 2014. Improvement of ray tracing algorithm based on linear traveltime interpolation[J].JournalofHunanUniversity:NaturalSciences, 41(1): 39--44 (in Chinese).

陆基孟， 王永刚. 2009. 地震勘探原理[M]. 第三版. 东营： 中国石油大学出版社: 47--53.

Lu J M, Wang Y G. 2009.ThePrincipleofSeismicExploration[M]. 3rd ed. Dongying: China University of Petroleum Press: 47--53 (in Chinese).

聂建新， 杨慧珠. 2003. 地震波旅行时二次/线性联合插值法[J]. 清华大学学报: 自然科学版, 43(11): 1495--1498.

Nie J X, Yang H Z. 2003. Quadratic/linear travel time interpolation of seismic ray tracing[J].JournalofTsinghuaUniversity:Science&Technology, 43(11): 1495--1498 (in Chinese).

田玥， 陈晓非. 2005. 水平层状介质中的快速两点间射线追踪方法[J]. 地震学报， 27(2): 147--154.

Tian Y, Chen X F. 2005. A rapid and accurate two-point ray tracing method in horizontally layered velocity model[J].ActaSeismologicaSinica, 27(2): 147--154 (in Chinese).

王辉， 常旭. 2000. 基于图形结构的三维射线追踪方法[J]. 地球物理学报, 43(4)： 534--541.

Wang H, Chang X. 2000. 3D ray tracing method based on graphic structure[J].ChineseJournalofGeophysics, 43(4): 534--541 (in Chinese).

徐涛, 徐果明, 高尔根, 朱良保, 蒋先艺. 2004. 三维复杂介质的块状建模和试射射线追踪[J]. 地球物理学报， 47(6): 1118--1126.

Xu T, Xu G M, Gao E G, Zhu L B, Jiang X Y. 2004. Block modeling and shooting ray tracing in complex 3-D media[J].ChineseJournalofGeophysics, 47(6): 1118--1126 (in Chinese).

张东， 谢宝莲， 杨艳， 傅相如， 秦前清. 2009. 一种改进的线性走时插值射线追踪算法[J]. 地球物理学报， 52(1): 200--205.

Zhang D, Xie B L, Yang Y, Fu X R, Qin Q Q. 2009. A ray tracing method based on improved linear traveltime interpolation[J].ChineseJournalofGeophysics, 52(1): 200--205 (in Chinese).

张建中， 陈世军， 余大祥. 2003. 最短路径射线追踪方法及其改进[J]. 地球物理学进展， 18(1): 146--150.

Zhang J Z, Chen S J, Yu D X. 2003. Improvement of shortest path raytracing method[J].ProgressinGeophysics, 18(1): 146--150 (in Chinese).

张建中, 陈世军, 徐初伟. 2004. 动态网络最短路径射线追踪[J]. 地球物理学报, 47(5): 899--904.

Zhang J Z, Chen S J, Xu C W. 2004. A method of shortest path raytracing with dynamic networks[J].ChineseJournalofGeophysics, 47(5): 899--904 (in Chinese).

赵爱华， 张中杰， 王光杰， 王辉. 2000. 非均匀介质中地震波走时与射线路径快速计算技术[J]. 地震学报， 22(2): 151--157.

Zhao A H, Zhang Z J, Wang G J, Wang H. 2000. A new scheme for fast calculation of seismic traveltimes and ray paths in heterogeneous media[J].ActaSeismologicaSinica, 22(2): 151--157 (in Chinese).

赵爱华， 徐涛. 2012. 提高规则网格最短路径方法反射波走时计算精度的走时校正技术[J]. 地球物理学进展， 27(5): 1854--1862.

Zhao A H, Xu T. 2012. A traveltime correction technique for improving the accuracy of reflection wave traveltimes with the shortest path method based on a regular grid[J].ProgressinGeophysics, 27(5): 1854--1862 (in Chinese).

赵改善， 郝守玲， 杨尔皓， 陈伟. 1998. 基于旅行时线性插值的地震射线追踪算法[J]. 石油物探， 37(2): 14--24.

Zhao G S, Hao S L, Yang E H, Chen W. 1998. Seismic ray tracing algorithm based on the linear traveltime interpolation[J].GeophysicalProspectingforPetroleum, 37(2): 14--24 (in Chinese).

Asakawa E, Kawanaka T. 1993. Seismic ray tracing using linear traveltime interpolation[J].GeophysicalProspecting, 41(1): 99--111.

Bai C Y, Huang G J, Zhao R. 2010. 2-D/3-D irregular shortest-path ray tracing for multiple arrivals and its applications[J].GeophysJInt, 183(3): 1596--1612.

Brodal G S. 2013. A survey on priority queues[G]∥Space-EfficientDataStructures,Streams,andAlgorithms. Heidelberg： Springer: 150--163.

Cardarelli E, Cerreto A. 2002. Ray tracing in elliptical anisotropic media using the linear traveltime interpolation (LTI) method applied to traveltime seismic tomography[J].GeophysicalProspecting, 50(1): 55--72.

Cormen T H, Leiserson C E, Rivest R L, Stein C. 2009.IntroductiontoAlgorithms[M]. 3rd ed. London: MIT Press: 151--169.

Julian B R, Gubbins D. 1977. Three-dimensional seismic ray tracing[J].JGeophys, 43(1/2): 95--113.

Moser T J. 1991. Shortest path calculation of seismic rays[J].Geophysics, 56(1): 59--67.

Qin F, Luo Y, Olsen K B, Cai W Y, Schuster G T. 1992. Finite-difference solution of the eikonal equation along expanding wavefronts[J].Geophysics, 57(3): 478--487.

Thurber C H, Ellsworth W L. 1980. Rapid solution of ray tracing problems in heterogeneous media[J].BullSeismolSocAm, 70(4): 1137--1148.

Vidale J. 1988. Finite-difference calculation of travel times[J].BullSeismolSocAm, 78(6): 2062--2076.

Xu T, Xu G M, Gao E G, Li Y C, Jiang X Y, Luo K Y. 2006. Block modeling and segmentally iterative ray tracing in complex 3D media[J].Geophysics, 71(3): T41--T51.

Xu T, Zhang Z, Gao E, Xu G, Sun L. 2010. Segmentally iterative ray tracing in complex 2D and 3D heterogeneous block models[J].BullSeismolSocAm, 100(2): 841--850.

Zhao A H, Zhang Z J, Teng J W. 2004. Minimum travel time tree algorithm for seismic ray tracing: Improvement in efficiency[J].JGeophysEng, 1(4): 245--251.

An improved ray-tracing algorithm based on linear travel-time interpolation

(CollegeofCivilEngineering,HunanUniversity,Changsha410082,China)

In order to solver for the problem that the original LTI algorithm could not trace the reverse propagation ray, several linear travel-time interpolation (LTI for short) improved algorithms, such as extension-compaction LTI algorithm, loop computation LTI algorithm, the shortest path ray tracing algorithm with dynamic networks, have been presented, but the computational efficiency of these algorithms are low. After analyzing these improved algorithms, this paper presented a new improved shortest path ray tracing algorithm with dynamic networks. According to the law of wave propagation and the basic equation of LTI, a large number of redundancy node calculation are excluded, and the traditional binary heap sort algorithm was used to manage node of wavefront array. The numerical examples show that, the improved algorithm presented in this paper has the highest computational efficiency among all of improved algorithms; its calculation efficiency is about 4.5—30 times of the shortest path ray tracing algorithm with dynamic networks, and about 2—6.5 times of the original LTI algorithm, and about 3.5—15 times of the shortest path ray tracing algorithm with dynamic networks when the traditional binary heap sort algorithm is also used.

ray tracing; linear traveltime interpolation; improved algorithm; wavefront expansion; computational efficiency

国家自然科学基金(51278182, 51408213)资助.

2013-12-27收到初稿， 2014-06-30决定采用修改稿.

e-mail: fangzhi@hnu.edu.cn

10.3969/j.issn.0253-3782.2014.06.010.

10.3969/j.issn.0253-3782.2014.06.010

P315.3+1

A

卢江波, 方志. 2014. 一种线性走时插值射线追踪改进算法. 地震学报, 36(6): 1089--1100.

Lu J B, Fang Z. 2014. An improved ray-tracing algorithm based on linear travel-time interpolation.ActaSeismologicaSinica, 36(6): 1089--1100. doi:10.3969/j.issn.0253-3782.2014.06.010.