基于层次分析法轴系校中多目标优化研究

肖能齐, 周瑞平, 林晞晨

(武汉理工大学 能源与动力工程学院， 湖北 武汉 430063)

基于层次分析法轴系校中多目标优化研究

肖能齐, 周瑞平, 林晞晨

(武汉理工大学 能源与动力工程学院， 湖北 武汉 430063)

在轴系合理校中过程中，目前仅仅是考虑单一目标函数进行最优化校中，而在实际校中过程中需要考虑多因素进行校中。本文考虑多目标因素下的合理校中,根据各目标对象所占的权重比，利用层次分析法求出满足轴系校中各项要求的轴承合理变位可行值。

轴系 多目标优化 层次分析法

1 前言

轴系校中问题，其最终是以轴承变位的形式出现的。目前，轴系进行合理校中采用的主要方法为试凑法，即根据直线状态下轴承负荷影响系数和自己的经验等来调整轴承的垂向位置，使之满足规范要求。近年来，随着计算机应用软件的发展，有许多学者对其进行研究。文献[1]采取以尾轴承最小为目标函数，将轴系校中优化处理为线性规划问题。文献[2]以中间轴承所承受的负荷最小为目标，通过中间轴承变位与主轴承变位的优化取值来进行求解最优解。文献[3]和文献[1]采用同样的目标函数，利用有限元法建立轴系校中模型，基于遗传算法对该问题进行求解。文献[4]主要针对低速柴油机推进轴系为研究对象设立目标函数，对主机轴承负荷进行优化。

上述文献通过MATLAB或VB等开发软件，在仅对某单一目标函数，而完全不考虑轴系校中过程中的其他因素能够求解得到最优解。在实际轴系校中过程中，不同类型船舶虽然都需要对多个因素进行综合考虑，但是选取的因素并不完全相同，同时各因素在校中过程中所占权重也不是同等重要。因此，本文以低速推进轴系校中为研究对象，在考虑多目标因素条件下，根据不同因素所占的权重，利用单纯形法和层次分析法相结合对轴系校中优化进行研究，使其更加符合实际需要。

2 合理校中的设计变量

轴系合理校中的核心任务就是求出各轴承合理的变位值，从而使得轴承的最佳负荷值满足规范要求，因此设定设计变量为

y=[Δy1,Δy2…Δyi…Δyn]

式中：Δyi为第i个轴承的垂向边位值，其中Δy1=0,Δy2=0。

3 合理校中的主要约束条件

在进行轴系合理校中，建立轴系校中数学模型解出轴系在直线状态下的各轴承负荷、轴段应力与弯矩和轴截面处的转角等。通过调整相应轴承的垂向变位值，使得各轴承的负荷等相关参数均达到最佳值。对推进轴系来说轴承负荷的变化量与垂向变位的关系可用轴系各轴承负荷影响系数矩阵来表示：

⟹

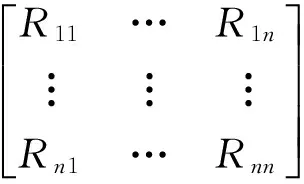
轴系合理校中是一个复杂的过程，需要考虑许多因素。轴系的合理校中可以归纳为具有线性约束的最优化问题。在轴系的合理校中过程中要满足如下技术要求[5]。

(1) 轴承的实际负荷不得超过设计或制造厂规定的允许值。

(2) 轴承中任一轴承负荷应为正值，而且轴承最小负荷应不小于轴承相邻两跨轴段所有重量总和的20%。

(3) 各轴截面上的附加弯曲应力不应超过设计规定的允许极限值。

(4) 对柴油机直接传动的轴系，计算时应确保作用在柴油机输出端法兰处的弯矩和剪力不超过制造厂规定的数值。

(5) 尾管后轴承支点处轴截面的最大转角不超过3.5 ×10-4rad或者不超过3.0 ×10-4rad[6]，否则需采取相应措施使之符合规定。

根据上述轴系校中的要求，轴系合理校中问题的主要约束条件有：

式中：Fi_min、Fi和Fi_max分别表示轴承i的最小许用负荷、实际负荷和最大许用负荷；Pi_min、Pi和Pi_max分别表示轴承i的最小比压、实际比压和最大比压；σ尾轴或螺旋桨轴、σ中间轴和σ推力轴分别表示螺旋桨轴、中间轴和推力轴最大弯曲应力；[σ尾轴或螺旋桨轴]、[σ中间轴]和[σ推力轴]分别表示螺旋桨轴、中间轴和推力轴许用弯曲应力；θ和θmax分别表示尾管后轴承支点处轴截面的转角(rad)和许用转角(rad)。

4 合理校中的目标函数

上述讨论了轴系校中的主要技术要求及轴实际约束条件，为使轴系校中更加合理，需要选取合适的目标函数，轴系合理校中时可供选择的目标函数有[1]：

(1) 后尾轴承负荷尽可能小。因为轴系螺旋桨的悬臂作用，全部轴承中后尾轴承受力最大，往往形成很严重的“边缘负荷"，其磨损也最大。所以为了确保轴系的正常运行，一般在校中计算中，应通过调整轴系中各轴承的变位，使尾轴后尾轴承负荷尽可能小。后尾轴承负荷受力最小F1(y)：

式中：F10为在直线状态下后尾轴承负荷；ΔF1为各轴承垂向变位对后尾轴承负荷影响的变化量之和。

(2) 主机后两道轴承负荷应尽量相同。由于主机的最后两道轴承相距太近，相互之间影响特别敏感，所以只有在轴承变位值恰当的时候轴承受力才会均衡。即

Δfj=|Fj-Fj+1|

式中：Fj为主机最后第一道轴承负荷；Fj+1为主机最后第二道轴承负荷。

(3) 主机各轴承变位值相等，且变位绝对值最小。为了在现场实际安装主机更加方便，在调整主机轴承垂向变位时最好整体下降。即

式中：Δyk+1为主机轴承的最小变位值。

(4) 中间轴承与主机最后一道轴承的负荷之差最小。因为中间轴承及主机最后一道轴承受轴系校中轴承变位的影响最大，所以：

Δfm=|Fm-Fm+1|

式中：Fm为中间轴承负荷；Fm+1为主机最后一道轴承负荷。

(5) 主机输出法兰处弯曲与剪力尽量不靠近静态许用负荷边界线。目标函数根据主机的静态负荷-弯矩图得到。

(6) 输出轴大齿轮前/后轴承负荷应尽量相同。在进行合理校中时，通常保证齿轮箱轴承受力均等，即

Δfi=|Fi-Fi+1|

式中：Fi为输出轴大齿轮后轴承负荷；Fi+1为输出轴大齿轮前轴承负荷。

对于低速机推进轴系和中高速机齿轮传动轴系在进行轴系校中过程中，选取目标函数的侧重点显然不一样。一般来说，对于低速柴油机往往更关注主机输出法兰处弯曲与剪力是否在许用范围内和中间轴承与主机最后一道轴承的负荷之差最小。而各船级社规定，对于中高速齿轮传动轴系侧重点是尽量保证齿轮箱输出轴前/后轴承负荷相等和尾轴后尾轴承负荷最小。本文将以低速机推进轴系为研究对象，同时考虑实际轴系校中的诸多因素进行最优化分析。

5 层次分析法

对于选取单一目标函数进行轴系校中，可以用通常解线性规划的单纯形法解出。单纯形法的主要思想就是先找一个基本可行解，判别其是否为最优解。如不是，就找一个更好的基本可行解，再进行检验。如此迭代进行，直至找到最优解,或者判定它无界。因此采用此方法，根据一个目标函数可以得到轴承变位值为

式中：yi为第i目标函数得到的各轴承变位值；yik为在第i目标函数下，第k个轴承的变位值。

通过前文的阐述可知，在实际轴系校中过程中目标函数和约束条件并不是单一的，而且各目标函数所占的权重不一样，单纯形法并不能解决问题。因此，需要本文通过层次分析法来解决该问题。

层次分析法(AHP法)是由美国运筹学家T.L.Saaty教授在20世纪80年代初提出的一种由两种比较过渡到多种比较的系统方法，亦是将半定性、半定量问题转化为定量问题的行之有效的方法。它是把定性方法和定量方法相结合的一种拟定量方法。它可以使人们的思维过程层次化，逐层比较多种关联因素，为分析、决策、预测或控制事物的发展提供定量依据。步骤如图1所示。

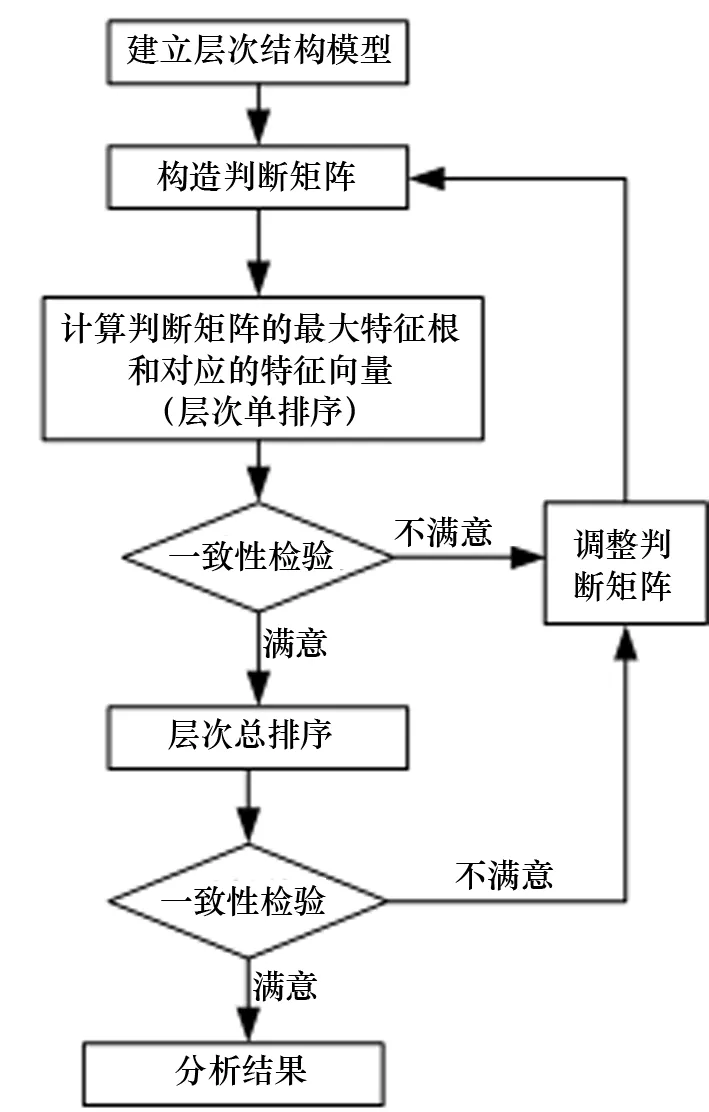
图1 步骤示意图

假设影响船舶推进轴系合理校中除考虑必要条件时，还与n个因素有关。即n个目标因素，分别用W1，W2，…，Wn来表示。为利于决策者对因素作出合理与正确的比较判断，将判断等级分为：同等重要、稍微重要、比较重要、明显重要、强烈重要和极端重要六个等级。仅仅从定性的角度区分影响船舶推进轴系合理校中任意两个因素之间的相对重要程度是远远不够的，所以需要利用AHP法将影响合理校中因素这个定性问题转化成定量问题。在进行轴系合理校中时，决策者会对每一层次中各因素相对重要性给出判断，这些判断通过引入合适的标度用数值表示出来，写成判断矩阵Q。因此，每一个判断矩阵的作用是在上一层某一个元素的约束条件下，对同层次的一组元素之间的相对重要性进行比较的结果。

在轴系校中过程中，计算者根据判断列出判断矩阵Q，计算满足QW=nW的特征根n及其对应的特征向量W，上式可写成：

式中：Wi/Wj为反映任意2个因素之间的相对重要程度。

T. L. Saaty教授提出如表1所示的指数标度。

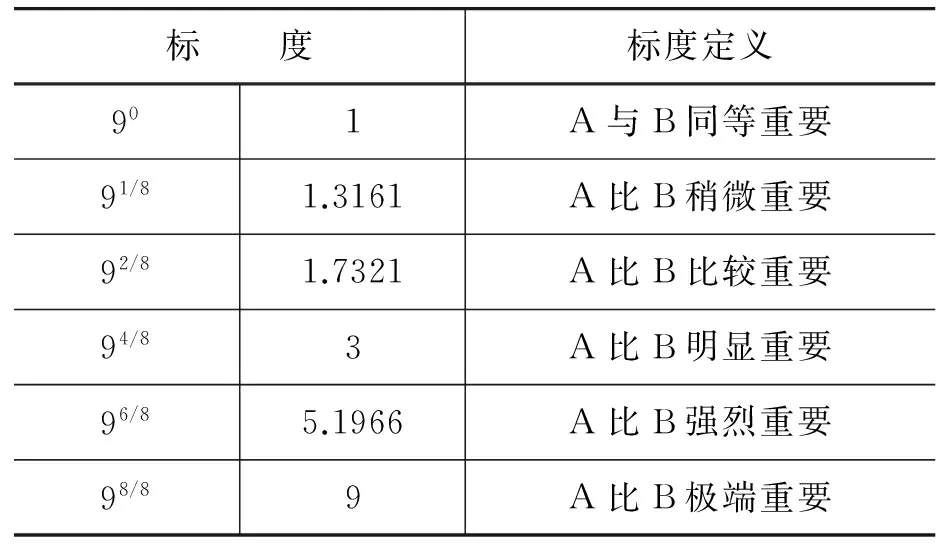
表1 判断矩阵标度及其含义

因此只要知道矩阵Q，从数学上求出Q的最大特征根及其特征向量，就能得到W=[q1…qi…qn]，即得到根据决策者对校中因素的排序结果。

Y=W[y1…yi…yn]

式中：Y为在合理轴系校中过程中引入层次分析法，很好地解决了多因素及各因素所占权重不同条件下的轴系校中最优化求解问题。

6 实例计算与分析

以某船厂生产制造的48 500 dwt货船轴系为研究对象，其推进轴系由桨轴(长：5 655 mm)、中间轴(长：6 160 mm)和MAN B&W 6S46MC-C8主机组成，螺旋桨轴基本轴径450 mm，中间轴基本轴径370 mm。除主机轴承外，还有前/后艉管轴承以及中间轴承。螺旋桨质量为11 576 kg，轴系布置简图如图2所示。此外，在热态(55℃)计算时考虑主机各轴承抬升量为0.21 mm。轴系简化为59个节点，58个梁单元，节点和单元编号从尾部开始。直线状态下，各轴承负荷如表2所示。

图2 轴系布置简图

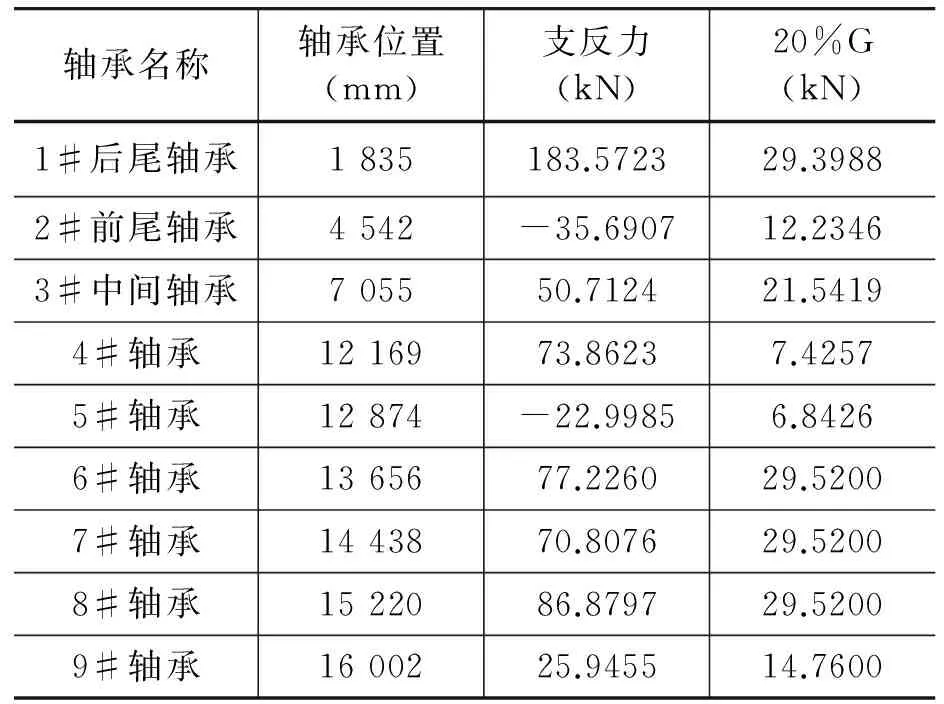
轴承名称轴承位置(mm)支反力(kN)20%G(kN)1#后尾轴承1835183.572329.39882#前尾轴承4542-35.690712.23463#中间轴承705550.712421.54194#轴承1216973.86237.42575#轴承12874-22.99856.84266#轴承1365677.226029.52007#轴承1443870.807629.52008#轴承1522086.879729.52009#轴承1600225.945514.7600

通过表2可知，2#前尾轴承以及5#轴承负荷均为负值，达不到船级社规范要求，所以需要对相应轴承进行调整使之符合规范要求。

6.1 设计变量的确定

根据如图2所示的轴系布置简图可知，为使各轴承负荷达到规范要求，需调整轴承的垂向位置，在此设定设计变量为

y=[Δy1,Δy2,Δy3,Δy4,Δy5,Δy6,Δy7,Δy8,Δy9]

式中：Δyi为第i个轴承的垂向边位值。

在进行轴系合理校中过程中，一般来说将前尾轴承/后尾轴承(1#轴承/2#轴承)放在轴线的理论中心线上，因此

Δy1=0,Δy2=0

即y=[0,0,Δy3,Δy4,Δy5,Δy6,Δy7,Δy8,Δy9]

6.2 目标函数及约束条件的选取

通过对该低速机推进轴系特点进行分析之后，本文拟选取以下目标函数进行轴系校中多目标研究。

除上述三个目标函数以外，根据船级社规范要求主机输出法兰处弯曲与剪力满足静态许用负荷作为一个目标函数，其目标函数对应的目标对象分别用A、B、C和D表示。

在对轴系校中进行最优化过程中，确定目标函数之后，轴系校中的主要约束条件需满足式(2)～(5)的要求。

对于上述四个目标函数利用单纯形法计算分别求解在约束条件下，热态时轴承合理的垂向变位值yA、yB、yC和yD，单位为mm，计算结果如表3所示。由于篇幅限制，在这里不列举除轴承负荷以外的其他相关数据。

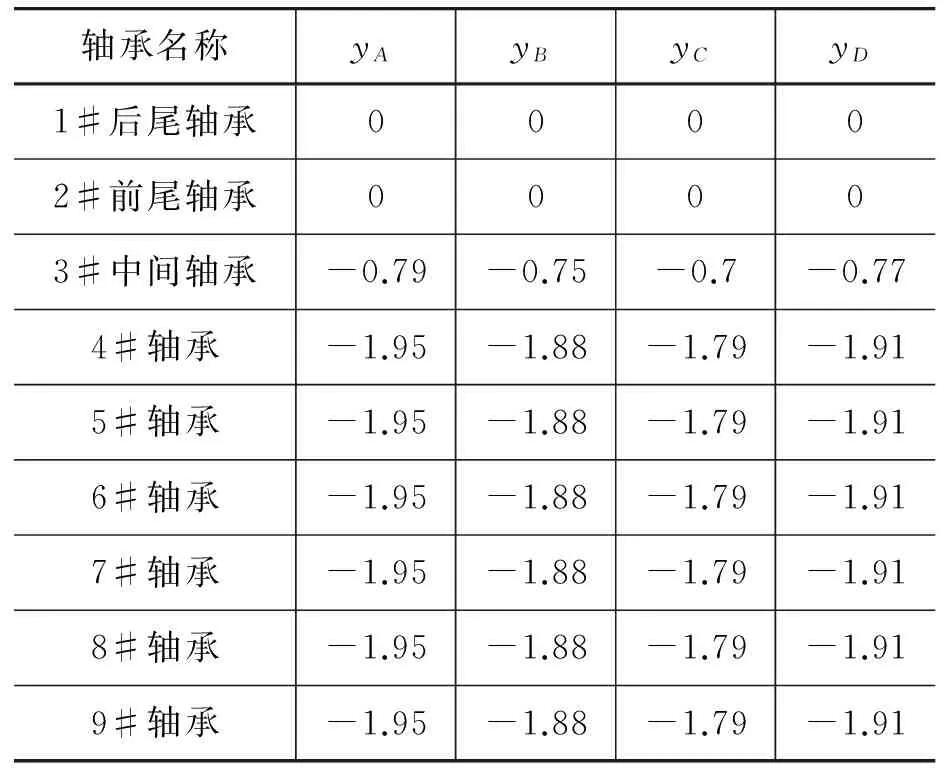
表3 轴承垂向变位结果

6.3 多目标优化

在实际轴系校中过程中，仅仅针对某一目标函数进行轴系校中显然是不够合理，而且由于A、B、C和D目标对象在实际校中过程中所占权重并不是同等重要，因此在该推进轴系校中过程中需要利用层次分析法进行综合分析。

由于对目标函数所对应的目标对象A、B、C和D四个因素的重要程度均不一样，所以利用层次分析法(AHP法)得到重要程度判断表4，进而根据表1得到判断矩阵标度，如表5所示。

表4 各种目标下轴承的负荷 单位：kN

表5 重要程度判断表

注：重要程度比较是行与列相比较，如：表中“强烈重要”是指A比B强烈重要。

根据表5判断矩阵标度可以得到矩阵Q：

接着求出矩阵Q的最大特征值以及最大特征值所对应的特征向量。为了显示各性能指标A、B、C和D占总指标的百分比，对各指标归一化后，即得各性能指标的权重值:

W=[0.4692 0.2239 0.2012 0.1058]

因此，根据单纯形法计算得到的各轴承变位值

[][]

(见表3)和式(14)，可以得到在考虑四个因素前提下最终变位值和热态下轴承负荷，如表6所示。

表6 考虑四个因素的最终变位值

7 结语

通过单纯方法和层次分析法进行编程，不仅可以考虑多目标因素，而且还可以根据不同目标因素所占的权重不一样，进行多目标因素综合轴系校中计算，其计算结果能满足校中的要求，具有很好的实用价值。

[1] 曹学涛. 船舶轴系校中的双向优化研究[D]. 大连: 大连理工大学, 2008.

[2] 陈金铭, 周海港, 顾卫俊, 马捷. 船舶推进轴系优化[J]. 船海工程, 2010, 39(3): 51-54.

[3] 汤金敏. 基于遗传算法的船舶推进轴系优化校中研究[J]. 湖南交通科技,2007,(03):132-134.

[4] 曹信来. 浅谈低速柴油机推进系统轴承负荷优化[J].船舶设计通讯,2010,(S2):55-58.

[5] American Bureau of Shipping. Rules For Building and Classing Steel Vessels[S]. 2009.

[6] DNV. Software-nauticus shaft align-ment user guide[S].2010.

Multi-objective Optimization of Shafting Alignment Based on AHP

XIAO Neng-qi, ZHOU Rui-ping, LIN Xi-chen

(Energy & Power Engineering School of Wuhan University of Technology,Wuhan Hubei 430063, China)

In the actual shafting alignment calculation, we often need to use many factors instead of a single objective function. In this article, multi-objective factors are taken into account in calculating the shafting alignment. According to the weight ratio of each factor, the feasible dislodgement value of bearing can be found based on AHP to meet the requirements of shafting alignment.

Shafting Multi-objective optimization AHP

肖能齐(1987-)，男，博士研究生。

U664

A