电动汽车用异步电机驱动控制系统可靠性分析

李 强， 王永全， 付瑶琴

(1. 中国卫星海上测控部，江苏 江阴 214400； 2. 西安交通大学 苏州研究院，江苏 苏州 215123)

0 引 言

能源危机和环境污染促进电动汽车的快速发展。电机驱动控制系统是电动汽车的核心，其可靠性直接影响电动汽车的安全性。电动汽车属于耐用型消费品，根据“浴盆曲线”理论，车辆使用后将从早期故障期向损耗期过渡，随着使用时间的延长，系统的可靠性将逐渐下降，零件磨损、陈旧引起设备故障率升高，维修活动和保障费用也会不断增加[1]。研究分析电动汽车电机驱动系统可靠性，以提高电动汽车的可靠性和安全性，从而减少了使用费和维修费，同时还减少了产品寿命周期的成本，提高了经济效益。

1 控制系统故障分析

常用于电动汽车的电机有直流电动机、异步电动机、永磁无刷电动机和开关磁阻电动机四类[2]。异步电机具有可靠性高、转矩波动小、费用低和噪声小等优点，被广泛用于电动汽车驱动系统[3]。本文主要对电动汽车用异步电机驱动控制系统可靠性进行分析研究。其驱动控制系统主要由主控制电路板、驱动逆变电路、蓄电池、传感器等元器件组成，结构框图如图1所示。该驱动控制系统的主要部件如图2所示。

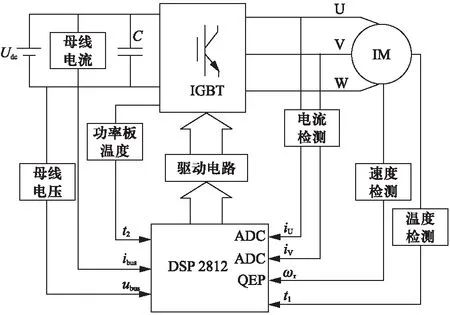
图1 异步电机驱动控制系统结构框图

图2 异步电机驱动控制系统的主要部件

1.1 电机故障模式分析

根据文献[4],在中小型异步电机中,轴承与绝缘故障占电机总故障数的97%，因此电机系统的薄弱环节为轴承系统和绝缘系统。

1.2 驱动控制系统故障模式分析

驱动控制系统将蓄电池的直流电转换为交流电，实现对电机的变频调速控制，主要由直流母线电容、大功率逆变器(IGBT)、驱动控制电路等组成。

1.2.1 直流母线电容

直流母线电容除了用于滤除整流器交流成分和稳定逆变器的供电电压之外，实际上更倾向于吸收逆变器产生的纹波电流，以降低直流母线阻抗，并抑制逆变器开关管开通、关断过程中产生的过冲电压。

纹波电流会带来电流或电压幅值的变化,由于是交流成分,会在电容上发生耗散。如果电流的纹波成分过大,超过了电容的最大容许纹波电流,会导致电容烧毁。因此，在驱动控制电路中，直流母线电容是一个薄弱环节。

1.2.2 大功率逆变器(IGBT)

大功率电机驱动的逆变器一般选择IGBT。IGBT是一种混合型电力电子器件，在高压、大电流、高速3方面是其他功率器件不能比拟的,因而在变流装置中被广泛应用。但是，过流、过压、过热都会损坏IGBT。在驱动控制电路中，IGBT是一个薄弱环节。

1.2.3 其他元器件

驱动控制电路主要由一些集成电路、功率管、电阻、电容等元件组成。在工作过程中，这些电子元器件因为过流、过压、过热等原因也经常发生故障。

2 可靠性模型

可靠性模型是指为预计或估算产品的可靠性所建立的数学模型。建立可靠性模型的目的和用途在于定量分配、估算和评估可靠性。经常用可靠度R(t)来描述产品的可靠性，指产品在规定的条件和时间内，完成规定功能的能力。

为了方便研究，在可靠性分析中考虑主要失效形式，忽略次要故障，主要对系统薄弱环节的可靠性进行分析。在分析过程中假设： (1) 电机与部件都只有两种状态，即故障状态和正常状态；(2) 各部件的故障相互独立。

在电机驱动控制系统中，当其中任一个单元发生故障，系统均不能正常工作。因此，可把电机驱动控制系统看成可靠性串联系统。系统可靠性模型框图如图3所示。

图3 驱动控制系统可靠性模型框图

2.1 轴承系统

电机轴承系统由两个轴承组成，只要其中一个轴承发生故障系统均不能正常工作。因此，轴承系统中两个轴承组成可靠性串联系统。可靠性框图如图4所示。图4中，R11、R12分别表示两个轴承的可靠度。

图4 轴承系统可靠性框图

研究表明，轴承的寿命服从威布尔分布，其概率密度函数f(t)和可靠度R1i(t)为

f(t)=αβ(t-γ)β-1e-α(t-γ)β

(1)

R1i(t)=e-α(t-γ)β

(2)

式中：α——尺度参数，α>0;

β——形状参数,β>0；

γ——位置参数,γ≤t。

为了简化研究，不考虑位置参数γ，则轴承的可靠度为

R1i(t)=e-α·tβ

(3)

对于球轴承β=10/9，圆柱滚子轴承β=3/2，圆锥滚子轴承β=4/3。α一般取轴承的特征寿命LRh，其与电机的转速、负载及电机质量等级有关。下面介绍α的计算方法。

在一定可靠度下，轴承寿命计算式[5]为

(4)

式中：LRh——轴承可靠度为R时的寿命，h；

n——电机转速，r/min；

C——滚动轴承额定负荷，N；

P——滚动轴承承受的当量动负荷，N；

ε——寿命指数，球轴承为3，圆柱滚子轴承为10/3；

a1——可靠度的寿命修正系数；

a2——材料修正系数,包括材料、设计和制造等影响因素；

a3——工作条件修正系数,包括润滑剂、润滑剂清洁度、逆向温度和装配条件等影响因素。

由上式可计算出对应一可靠度R(t0)时的轴承寿命t0,将R(t0)、t0带入轴承可靠度计算式(3)，即可计算出α，从而可以获得轴承的可靠度数学模型。

两个轴承可靠度是串联模型，则轴承系统的可靠度为

R1(t)=R11(t)·R12(t)=e-(α1·tβ1+α2·tβ2)

(5)

2.2 绝缘系统

电机绝缘系统主要由匝间绝缘、相间绝缘、槽间绝缘组成，当其中之一发生故障电机均不能正常工作，因此组成串联可靠性模型。其可靠性框图如图5所示。图5中，R2i(i=1、2、3)分别为匝间绝缘、相间绝缘、槽间绝缘可靠度。

图5 电机绝缘系统可靠性框图

研究表明匝间绝缘、相间绝缘、槽间绝缘都近似服从指数分布，其概率密度函数f(t)和可靠度R2i(t)为

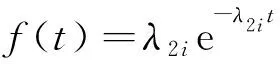
(6)

R2i(t)=e-λ2it(i=1、2、3)

(7)

λ2i与电机运行温度、绕组线径、绝缘等级、工艺和引线焊接材料等有关。文献[6]给出了λ2i的计算模型：

λ2i=λbπEπQπKπC

(8)

式中：λb——基本失效率；

πE——环境系数；

πQ——质量系数；

πK——种类系数；

πC——结构系数。

基本失效率λb的计算式为

(9)

式中：THS——热点温度；

NT——温度常数；

G——加速常数；

A——失调率调整系数。

上述参数可根据电机的运行状态查文献[6]获得。

绝缘系统的可靠度为

(10)

式中，λ2i(i=1、2、3)分别代表匝间绝缘、相间绝缘、槽间绝缘的失效率。

2.3 直流母线电容系统

直流母线电容系统由3个大电容构成，当其中任何一个电容发生故障，系统均不能正常工作。因此，直流母线电容组成可靠性串联模型。其可靠性框图如图6所示。图6中，R3i(i=1、2、3)分别表示3个电容的可靠度。

图6 直流母线电容系统可靠性框图

大量研究表明，大电容器的寿命近似服从指数分布，其可靠度为

R3i(t)=e-λ3it(i=1，2，3)

(11)

λ3i(i=1，2，3)为母线电容工作失效率，文献[6]给出了λ3i的计算模型为

λ3i=λbπEπQπCV

(12)

式中：λb——基本失效率，10-6/h；

πE——环境系数；

πQ——质量系数；

πCV——电容量系数。

电容器基本失效率λb的模型为

(13)

式中：A——失效率水平调整系数；

S——工作电压与额定电压之比；

Ns——应力常数；

T——工作环境温度；

NT——温度常数；

B——形状参数；

G——加速常数。

上述参数可以根据电容器的参数及工况在文献[6]中查表获得。

直流母线电容系统的可靠度为

(14)

2.4 大功率逆变电路(IGBT)

IGBT是由MOSFET和双极型晶体管复合而成的一种电子器件，其输入极为MOSFET，输出极为PNP晶体管，融和了这两种器件的优点，具有良好的工作特性和高可靠性，被广泛应用与电机驱动控制逆变电路。在电机驱动控制系统中要用到3个大功率逆变元器件，一般选择3个IGBT。当其中任何一个发生故障时，系统均不能正常工作，因此组成可靠性串联模型。其可靠性框图如图7所示。图7中，R4i(i=1、2、3)分别是3个IGBT的可靠度。

图7 IGBT系统可靠性框图

大量研究表明，IGBT寿命近似服从指数分布，其可靠度为

R4i(t)=e-λ4it

(15)

λ4i为IGBT工作失效率，目前还没有统一的计算方法。本文根据其内部结构和工作方式，在文献[6]基础上提出了λ4i的计算模型。

λ4i=πQC1πTπV+(C2+C3)πEπL

(16)

式中：λ4i——工作失效率，10-6/h；

πQ——质量系数；

πT——温度应力系数；

πV——电压应力系数；

πE——环境应力系数；

πL——成熟系数；

C1、C2——电路复杂度失效率；

C3——封装复杂度失效率。

上述的参数可查文献[6]获得。

大功率逆变系统的可靠度为

(17)

2.5 驱动控制电路

驱动控制电路由大量集成电路芯片、电阻、电容、电子管、电位器、继电器、感性元件等组成。大量研究表明，电子元器件的寿命均服从指数分布。可靠度为

R5i(t)=e-λ5it(i=1，2…，n)

(18)

n为驱动控制电路所有电子元件数、印制板孔数以及焊接点数之和。

驱动控制电路系统可靠度为

(19)

λ5i是各电子元件的工作是效率，文献[3]给出了各种电子元器件的工作失效率λ5i的计算模型，具体如下。

(1) 集成电路芯片。

集成电路芯片的工作失效率模型为

λ=λbπEπQπLπTπF

(20)

式中：λb——基本失效率；

πE——环境系数；

πQ——质量系数；

πL——成熟系数；

πT——温度应力系数；

πF——电路功能系数。

基本失效率λb模型为

λb=ASλC+λRTNRT+∑λDCNDC+λSE

(21)

式中：AS——衬底面积；

λC——网络复杂度失效率；

NRT——膜电阻数；

λRT——膜电阻失效率；

NDC——外贴元件数；

λDC——外贴元件失效率；

λSE——为工艺封装失效率。

(2) 半导体分立器件。

半导体分立器件包括晶体管、二极管、光电子器件，其工作失效率为

λ=λbπEπQπAπS2πτπC

(22)

式中：λb——基本失效率；

πE——环境系数；

πQ——质量系数；

πA——应用系数；

πS2——电压应力系数；

πτ——额定功率因数；

πC——结构系数。

基本失效率λb模型为

(23)

式中：A——失效率水平调整系数；

NT、P——形状参数；

TM——最高允许结温，K；

T——工作环境温度,℃；

ΔT——TM与满额时最高允许温度(TS)的差值，℃；

S——工作电应力与额定电应力之比。

(3) 电阻器。

电阻器的一般失效率模型为

λ=λbπEπQπR

(24)

式中：λb——基本失效率；

πE——环境系数；

πQ——质量系数；

πR——阻值系数。

基本失效率λb模型为

(25)

式中：A——失效率水平调整参数；

B——形状参数；

T——工作环境温度；

NT——温度常数；

G、J、H——加速常数；

NS——应力常数；

S——工作功率与额定功率之比。

(4) 电容器件。

电容器件的可靠度计算方式参考直流母线电容可靠性模型。

(5) 印制板。

印刷版的一般失效率模型为

λ=λbNπEπQ

(26)

式中：λb——基本失效率；

πE——环境系数；

πQ——质量系数；

N——印制板孔数。

(6) 焊点。

焊点的一般失效率模型为

λ=λbπE

(27)

式中：λb——基本失效率；

πE——环境系数。

3 电动汽车驱动控制系统可靠性预计

基于建立的电动汽车驱动系统可靠性模型，采用应力分析法对15kW电动汽车用感应电机驱动控制系统可靠性进行分析。工作环境温度为30℃，以下计算工作失效率单位均是10-6/h，时间t的单位为106h。

3.1 电机轴承系统可靠度

所选电机采用的轴承为100型深沟球轴承，转速n=5600r/min,额定动载荷C=4270N，轴承动负荷P=138N，球轴承时ε=3，计算可靠度为0.9时的寿命，可靠度寿命修正系数a1=1，材料修正系数a2=1.2，工作条件修正系数a3=1.1，则根据式[4]可得，LRh=0.11638，带入轴承可靠度计算式可得α=1.1497，则轴承系统可靠度为

R1(t)=R11(t)·R12(t)=e-2.299 4·t10/9

(28)

3.2 绝缘系统可靠度

本文所选电机绝缘等级为F级，经温升计算的热点温度为85℃，查文献[6]可得：λb=0.019，πE=5，πQ=4，πK=1，πC=1，则绝缘绕组的工作失效率为

λ2i=λbπEπQπKπC=0.38(i=1,2,3)

(29)

绝缘系统的可靠度为

(30)

3.3 直流母线电容可靠度

直流母线电容系统由3个电容值为 2200uF，耐压值为400V的美国CDE DCMCE-1666螺栓式铝电解电容并联组成。查文献[6]可得πE=1，πCV=1.9,πQ=0.1，λb=0.1862，则

λ3i=λbπEπQπCV=0.0354(i=1，2，3)

直流母线电容系统可靠度为

(31)

3.4 大功率逆变电路(IGBT)可靠度

本文控制系统选用的功率开关器件为三菱公司的CM300DY-12NF IGBT模块，使用三组并联。根据文献[6]可得πE=1，πQ=0.25，πT=3.78，πV=1，C1=0.118，C2=0.015，C3=0.019，πL=1。计算得λ4i=πQC1πTπV+C2+C3πEπL=0.12。则IGBT系统的可靠度为

(32)

3.5 控制电路板可靠度

控制板是一块4层金属印制板，其中包括22个集成电路芯片，32个半导体分立器件，118个电阻器件，96个电容器件，546个焊点，若其中一个元器件发生故障，系统不能正常工作，组成可靠性串联模型。根据文献[6]可计算每个元器件的工作失效率，从而可获得控制电路板的工作失效率λ5=12.258。则控制板可靠度为

R5(t)=e-λ5t=e-12.258 t

(33)

3.6 系统整体可靠度

由可靠性模型计算可得，电动汽车用异步电机驱动控制系的可靠度为

(34)

若取t=1000，可得平均无故障时间为1000h 时，系统可靠度为R(0.001)=0.985。

4 结 语

本文对电动汽车用异步电机驱动控制系统的故障模式进行分析，找出系统薄弱环节，在系统设计时给薄弱环节分配较高的可靠度。在此基础上建立系统可靠性数学模型，对系统可靠性进行了分析和预计，可以获得平均无故障工作时间以及指定时间下的可靠度等指标。通过提高系统薄弱环节可靠度和预计系统整体可靠性，可有效提高系统的可靠度和安全性，降低故障率，减少了使用费和维修费，同时还减少了产品寿命周期的成本，提高了经济效益。

【参考文献】

[1] 姜兴渭，宋正吉，王晓晨.可靠性工程技术[M].哈尔滨： 哈尔滨工业大学出版社，2005.

[2] 闰大伟,陈世元.电动汽车驱动电机性能比较[J].汽车电器,2004，39(4)： 4-6.

[3] ZERAOULIA M, BENBOUZID M E H, DIALLO D. Electric motor drive selection issues for HEV propul-sion systems： a comparative study[J]. IEEE Transactions on Vehicular Technology, 2006,55(6)： 1756-1764.

[4] EMANUEL B. Life expenctancy of motors[J]. IEEE Electrical Insulation Magazine, 1991,7(6)： 14-22.

[5] 成大先.机械设计手册[M].北京： 化学工业出版社，2004.