基于STF的永磁同步电机无传感器SVM-DTC系统
张少华, 郭 磊
(1. 中国船舶重工集团公司第七一二研究所,湖北 武汉 430064; 2. 华中科技大学武昌分校, 湖北 武汉 430064)
0 引 言
永磁同步电机(Permanent Magnet Synchro-nous Motor, PMSM)具有结构简单、运行可靠、体积小、重量轻、效率高等优点,在要求高控制精度、高可靠性的场合获得了广泛应用。转速、位置信号是电机获得高精度控制的前提,机械式传感器增加了控制系统的成本,降低了系统的整体可靠性。高精度无速度传感器控制成为近年来研究的热点[1]。
扩展卡尔曼滤波(Extend Kalman Filter,EKF)是一种应用于非线性系统的状态最优估计方法,其用EKF构建永磁电机的状态观测器来估计电机的转速、位置信号。但大多数情况下,EKF只能给出状态的有偏估计,当实际系统参数产生变化时,对模型误差的鲁棒性较差。为获得更好参数估计,可以利用强跟踪滤波器(Strong Tracking Filter, STF)来实现电机转速估计。STF与EKF相比,有以下优点[2]: (1) 对于模型的初始状态和系统测量噪声的统计性质不敏感;(2) 在滤波器达稳态时,对过程的突变状态仍具有很强的跟踪能力;(3) 计算量与EKF相当。
本文在永磁同步电机直接转矩控制系统中,采用STF构建电机转速、定子磁链观测器,以实现电机参数的实时在线观测;在逆变器的调制方法上,采用空间矢量调制(Space Vector Modulation, SVM)取代传统的电流滞环控制,以降低磁链和转矩脉动,分别构建基于STF观测器和EKF观测器的永磁同步电机直接转矩控制模型。在外界扰动及模型发生变化等情况下,对两种算法进行仿真比较,验证了算法的可行性和有效性。
1 永磁同步电机数学模型[3]
静止两相α、β坐标系中,对于面装式PMSM来说,理想状态下的电机电压、磁链、转矩方程如式(1)~式(3)所示。
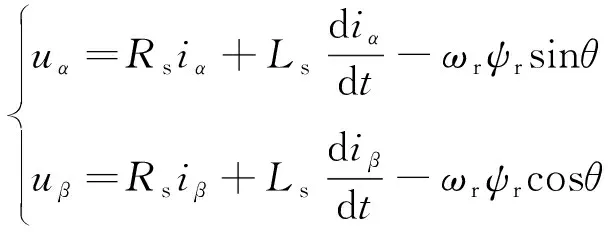
(1)

(2)
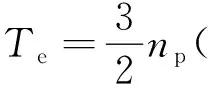
(3)
式中:uα、uβ——定子电压的α、β坐标分量;
Rs——定子电阻;
iα、iβ——定子电流的α、β坐标分量;
Ls——定子电感;
ωr——电机转速;
ψr——转子磁链。
联立式(1)和式(2),可得

(4)
转矩方程改写成在d、q坐标系中,有

(5)
其中,δsm为定子磁链与转子永磁体产生的磁链之间的夹角,即转矩角。
对于面装式PMSM来说,Lq=Ld,故式(5)改写为

(6)
由式(6)可知,若保持定子磁链幅值恒定,由于转子磁链幅值为常数,可通过控制转矩角来实现转矩的动态控制。
2 基于STF观测器的永磁同步电机SVM-DTC系统[4]

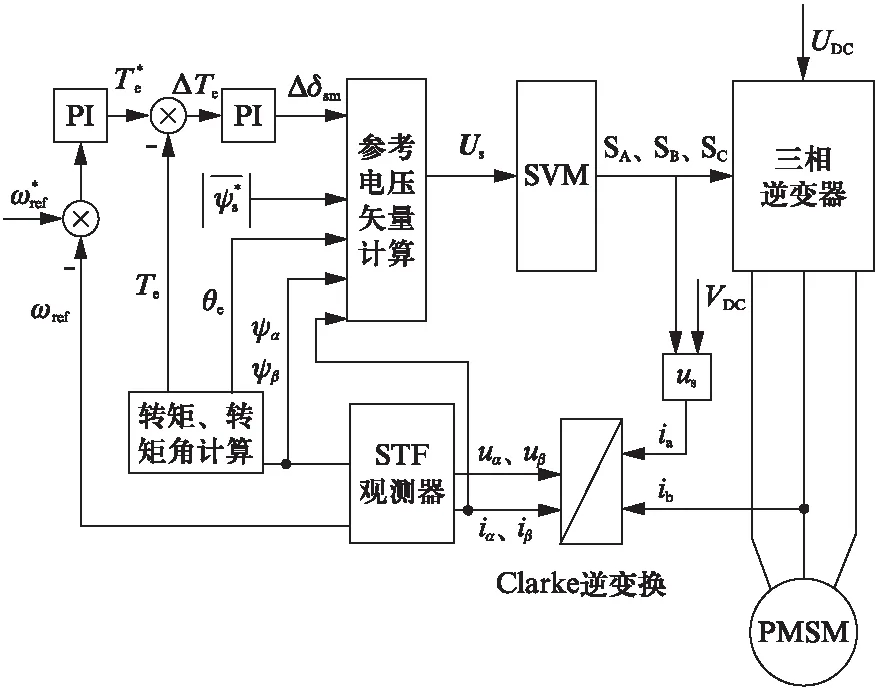
图1 基于STF观测器的永磁同步电机SVM-DTC系统图
2.1 参考电压矢量的计算
由式(7)、式(8)和式(3)可得出估计的定子磁链的幅值、角位置和电磁转矩。由式(9)得出定子磁链和给定的磁链矢量的偏差。设系统给定采样时间为Ts,结合式(10)、式(11)、式(12),可得SVM当前所需的参考电压矢量Uref。

图2 定子磁链空间矢量图
(7)
(8)
(9)
(10)
(11)

(12)
2.2 SVM原理[5]
SVM是将电机和逆变器看成一个整体,靠电压空间矢量的相加来实现电机转动所需的圆形旋转磁场。对于三相电压源逆变器来说,一共有8种开关状态,对应8个电压空间矢量。SVM原理图如图3所示。

图3 SVM原理图
图3中,以第3扇区的任一给定矢量Usf为例,有
(13)
式中: U4、U6——两个相邻的工作电压矢量;
T4、T6——相对应的电压矢量作用时间;
T0——U0或U7的作用时间。
可得
(14)
给定电压矢量表示为
T4+T6≤T
(15)
联立式(13)~式(15),可得

(16)
相对于其他调制方式,采用空间矢量调制的逆变器实际开关次数较少,最大开关电流较低,开关损耗较小,直流母线电压利用率更高。
3 PMSM的STF观测器设计
3.1 STF原理[2]
强跟踪滤波算法是由周东华教授90年代在EKF的基础上提出。
考虑一类离散时间非线性系统,如式(17)所示。

(17)
式中:x——系统状态变量,x∈Rn;
k——离散时间变量,k∈N;
u——输入变量,u∈Rp;
y——输出变量,y∈Rm。
非线性函数f:Rn和h:Rm对x有连续的偏导数,过程噪声wk是n维方差为Qk的高斯白噪声,测量噪声vk是m维方差为Rk的高斯白噪声。
上述系统的强跟踪滤波器如下。
(1) 一步状态预报值。

(18)
(2) 滤波增益值。
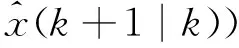
(19)
(3) 状态估计值。
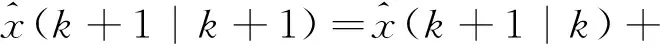
(20)
(4) 预报误差协方差。

(21)
(5) 状态估计误差协方差阵。

(22)
(6) 残差序列。
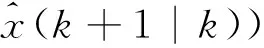
(23)
以上各式中,

(24)
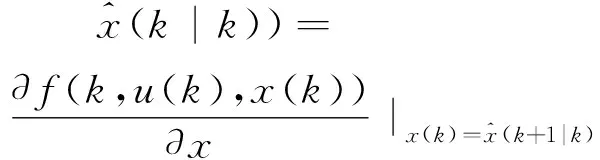
(25)
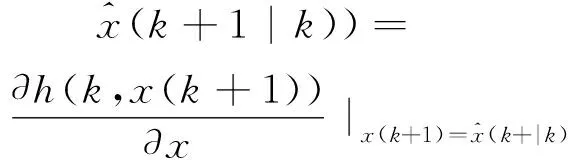
(26)
对于式(17)所示离散非线性系统,采用正交原理,在EKF的基础上,在预测误差方差方差中引入一个多重次优的渐消因子λ(k+1),可将式(22)改写为

(27)
其中,渐消因子由下式确定

(28)
(29)
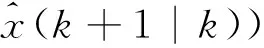
(30)

(31)
(32)
其中,遗忘因子ρ=0.95,其作用是对旧数据进行渐消从而突出新残差的影响,进一步提高滤波器的跟踪能力。预先选定的弱化因子β≥1,目的是使状态估计值更加平滑,其值可根据经验选取,本文选β=4.5。
3.2 PMSM的STF观测器设计[6]
由电机的状态方程可知离散控制系统的采用时间间隔非常小,且系统的机械时间常数一般远大于电磁时间常数,所以认为在采样期间电机转速恒定不变,电机转速的导数为零。选取状态变量x=[ψαψβωrθr]T,输入变量u=[uαuβ]T,输出变量y=[iαiβ]T。构建状态方程和输出方程为

(33)
设采样周期为Ts,对式(33)离散化,并考虑到控制系统的动态噪声w(k)和测量噪声v(k+1),可得

(34)
式中,k为整数,且k≥0,则
f(k,x(k),u(k))=

(35)

(36)
STF递推算法可实现PMSM的STF观测器设计,得到每个采样周期内系统的状态估计值。
4 仿真及结果分析
为验证基于STF观测器和SVM的永磁同步电机直接转矩控制系统的可行性和有效性,在MATLAB/Simulink仿真环境下建立了系统的仿真模型。STF算法通过s函数实现,STF的参数选取为


其中,仿真采用的电机参数:定子电阻为2.875Ω,定子d、q坐标下的电感Ld、Lq为0.0085H,永磁体产生的磁场为0.175Wb,转动惯量为0.0008kg·m2,电机的极对数为4。
转速给定为100r/min,在0.3s时突加3N·m的负载,分别采用EKF观测器估算[7]和STF观测器估算的磁链估算波形、转速估算波形、转速估计误差波形、转矩波形、转子位置估算波形分别如图4~图8所示。从图中对比可以看出,在电机突加给定空载起动后,两种估算方法的转速均能较快达到给定转速。在起动的动态过程中,STF能较快速地估计电机的各状态参数,而EKF的估计存在较大的动态跟踪误差;稳定运行时,两种算法都能准确估计电机各状态参数。当电机运行达到0.3s时,突加负载引起状态发生变化,EKF算法产生的跟踪误差明显比STF算法的脉动大,跟踪状态变化的能力相对STF较差,而STF则能很快跟踪电机状态变化,动态跟踪精度高。仿真结果说明,STF观测器能较准确地估算出电机的转速、定子磁链等参数,且系统的抗扰动性能较EKF更强。
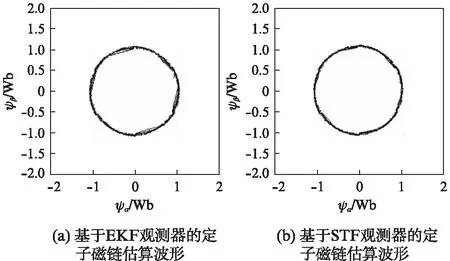
图4 给定转速下的定子磁链估算波形

图5 给定转速100r/min下的转速估算波形

图6 给定转速100r/min下的转速估计误差波形

图7 给定转速100r/min下的转矩估计误差波形

图8 给定转速100r/min下的转子位置估算波形
以上是在电机模型未发生变化的情况下进行的仿真比较,但实际情况下,系统在复杂环境下,可能会存在各种随机的噪声干扰,测量时也存在着随机干扰,系统的噪声和测量噪声的协方差矩阵可能发生变化。在系统空载,转速给定为120r/min时,系统噪声协方差矩阵Qk、Rk发生变化时的转速波形如图9所示。其中,Qk、Rk分别变为



图9 给定转速120r/min下,噪声协方差变化时的转速波形
由图9可以看出,当系统噪声协方差矩阵Qk、Rk发生变化时,基于STF观测器的系统转速稳定,波形受到的干扰小,而EKF的波形受到的干扰较大。
5 结 语
为减小传统直接转矩控制方式下,电流滞环控制转矩和磁链脉动较大的问题。本文在永磁同步电机直接转矩控制系统中,采用SVM取代传统的电流滞环控制,以降低磁链和转矩脉动;为提高系统快速跟踪能力及抗扰动性能,采用STF构建电机转速、定子磁链观测器,以实现电机参数的实时在线观测。为验证算法的可行性,分别构建了基于STF观测器和EKF观测器的永磁同步电机直接转矩控制仿真模型。在外界扰动及模型发生
变化等情况下对两种算法进行仿真比较。结果表明,STF能准确观测出电机的动态参数,并且系统的抗扰动性能较EKF更强。
【参考文献】
[1] 王鑫,李伟力,程树康.永磁同步电机发展展望[J].微电机,2007,40(5): 69-72.
[2] 周东华.非线性系统的自适应控制导论[M].北京:清华大学出版社,2002.
[3] 李崇坚.交流同步电机调速系统[M].北京: 科学出版社,2006.
[4] 徐艳平,钟彦儒,于宏全.基于MATLAB的永磁同步电机直接转矩控制的仿真建模[J].微电机,2005,33(3): 27-30.
[5] 郎宝华,刘卫国,周熙炜,等.空间矢量脉宽调制的仿真研究及应用[J].电机与控制应用,2007,34(8): 9-12.
[6] XIE X Q, ZHOU D H, JIN Y H. Strong tracking filter based adaptive generic model control[J]. Journal of Process Control, 1999,9(4): 337-550.
[7] 陈振,刘向东,靳永强.采用扩展卡尔曼滤波磁链观测器的永磁同步电机直接转矩控制[J].中国电机工程学报,2008,28(33): 75-81.

