定子无磁轭模块化轴向永磁电机的优化设计*

周 涛，黄允凯，董剑宁，李 浩

(东南大学电气工程学院，江苏南京 210096)

0 引言

轴向永磁电机因其结构紧凑、效率高、功率密度大等优点备受国内外研究人员关注[1]，尤其适用于电动车辆、可再生能源系统和工业设备等要求高转矩密度和空间紧凑的场合[1，2]。

轴向永磁电机的优化设计是一个复杂的非线性、有约束、多变量、多维度的工程规划问题。电机传统的优化设计方法主要有直接搜索法和随机搜索法两种寻优模式。其中，应用较广泛的有Powell法、单纯形法和梯度法等[3]。传统优化设计方法的弊端是全局寻优能力较差，难以应用于复杂的工程实际问题。近年，基于遗传算法的新型全局优化算法在永磁电机优化设计中得到广泛应用。文献[4]采用遗传算法和有限元分析相结合，设计了一台1 kW轴向永磁电机，实现最大功率密度优化。文献[5]在电机基本尺寸方程的基础上，通过遗传算法优化得到较高功率密度，但没有考虑效率、经济性等其他性能指标的多目标优化。文献[6]提出了一种同时考虑电磁和机械约束的轴向永磁电机遗传算法优化设计，使材料成本最低，但没有考虑对反电动势、效率等相关性能指标的影响。文献[7]采用遗传算法实现一台4极15槽轴向永磁电机最大功率密度优化，并对反电动势总谐波失真进行分析。文献[8]提出了基于遗传算法实现齿槽转矩抑制和平均转矩提高的多目标优化设计，应用排列选择法求解多目标Pareto最优解。可看出，相关文献多针对诸如功率密度、成本等性能指标进行单目标优化设计。多目标优化对于电机实际应用的意义明显，是轴向永磁电机优化设计的重要研究方向。

遗传算法起源于对生物系统所进行的计算机模拟研究，是一种基于生物遗传和进化机制的适合于复杂系统优化的自适应概率优化技术。其本质是一种高效、并行、全局搜索的方法，能够在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以获取最优解。电机优化设计是复杂的约束非线性问题，适合于应用遗传算法来实现最优寻解。

本文提出一种新型结构的轴向永磁电机，应用于电动车辆再生制动系统，采取遗传算法优化策略实现包括效率、功率密度、经济性在内的多目标优化设计，并采取措施减小齿槽转矩，获得正弦度高的反电动势波形。

1 电机模型和尺寸方程

1.1 电机模型

轴向永磁电机结构形式多样，通常设计成单边、双边和多盘式结构[1]。双边轴向永磁电机具有实用前景，分为双定子单转子和双转子单定子两种结构形式。双定子单转子结构可以减少永磁体的使用量，但绕组损耗较大。双转子单定子型轴向永磁电机具有转矩体积比大、机械鲁棒性好、功率密度高等优良性能，相较其他结构获得更多的应用。本文在双转子单定子结构的基础上，提出了一种定子无磁轭、模块化的新结构轴向永磁电机用于电动车辆再生制动系统。定子无磁轭模块化轴向永磁电机结构如图1所示。

图1 定子无磁轭模块化轴向永磁电机结构

轴向永磁电机采用双转子单定子结构，定子放置在中间，与两个外转子组成双气隙。永磁磁极按N、S极性交替排列贴在转子表面，两侧永磁体N、S对等放置，电机结构高度对称，有效避免了单边磁拉力等问题。轴向永磁电机气隙呈平面型，气隙磁场沿轴向分布。磁路结构示意图如图2所示。

图2 磁路结构示意图

定子采用模块化结构，定子无磁轭且由若干个相同的小模块组成，可简化轴向永磁电机的制造和装配过程。小模块中铁心可由硅钢片堆叠，也可采用软磁复合材料或者非晶合金等新型材料制作，绕组直接绕在铁心外的绝缘材料上。该结构的轴向永磁电机定子铁耗小、绕组端部短、槽满率高，有助于提高电机的功率密度和效率。此外，无磁轭结构也使得定子铁心重量减轻。

1.2 尺寸方程

在定子漏磁电感和电阻忽略不计情况下，轴向永磁电机的输出功率可表示为[9]

式中:η——电机效率;

m——电机相数;

T——反电动势周期;

Epk——相反电动势峰值;

Ipk——相电流峰值;

Kp——电功率波形系数。

轴向永磁电机尺寸方程为

式中:KΦ——转子电负荷和定子电负荷的比值;

ml——每个定子的相数;

Ke——电动势系数;

Ki——电流波形系数;

Bg——气隙磁密;

A——电负荷;

f——电机频率;

p——电机极对数;

λ——电机的内外径之比;

Do——电机外直径;

Le——电机的轴向有效长度。

轴向永磁电机的整体功率密度为

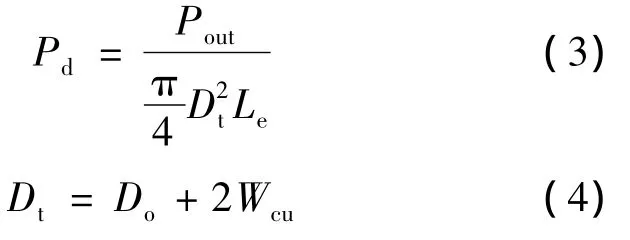
式中:Wcu——两端绕组端部单边长度;

Dt——电机的总体外直径。

对于双转子轴向永磁电机，电机的轴向长度为

式中:F(X)——优化目标函数;

式中:Lr——转子的轴向长度;

Ls——定子的轴向长度;

g——气隙长度。

转子的轴向长度是转子铁心长度Lcr和永磁体厚度Lpm之和，即

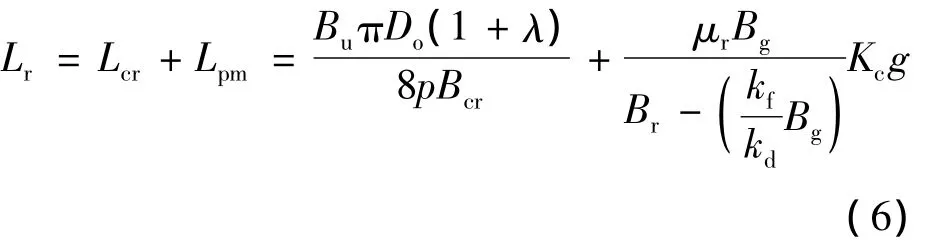
式中:Bu——永磁体表面的磁通密度;

Bcr——转子铁心磁通密度;

μr——永磁体相对磁导率;

Br——永磁体剩磁密度;

kf——气隙磁密校正系数;

kd——漏磁系数;

Kc——卡式系数。

定子的轴向长度取决于气隙磁通密度、定子铁心中的磁通密度，以及电机内外径等，即

式中:αp——平均气隙磁通密度和峰值气隙磁通密度的比值;

Bcs——定子铁心的磁通密度。

2 遗传算法

2.1 基本原理

从电机的基本尺寸方程可知，轴向永磁电机的设计是一个高度的非线性化问题，诸多参数之间都有紧密的联系。遗传算法适合求解复杂的非线性问题，模拟自然选择过程中发生的复制、交叉和变异等现象，通过编码操作将待求问题空间映射到编码空间，从任意初始种群出发，通过随机选择、交叉和变异操作及其循环迭代，搜索编码空间内的最优解，再映射到原问题空间，求得原问题的最优解。

遗传算法运算流程如图3所示。遗传算法的实现主要步骤:染色体编码、初始种群的产生、个体适应度评估、遗传算子设计、遗传终止判定。

图3 遗传算法运算流程

遗传算法同时处理种群中的多个个体，对搜索空间内的多个解进行评估，使得算法具有良好的全局搜索性能，并易于并行化。遗传算法可以同时改变多个参变量取值，易于实现多目标函数在全局范围内最优寻解。

2.2 目标函数

在电机的优化设计中，电机的各项技术指标可表示为所选取的优化设计变量的函数，作为优化设计中的约束限定条件。电机的优化目标也是优化设计变量的函数。电机优化设计问题可归结为约束化的非线性数学模型(8)。

X——优化设计变量;

n——优化设计变量总数;

G(X)——约束条件函数;

m——约束条件总数。

本文选取功率密度、效率、经济性作为优化设计的目标函数，实现多目标优化设计。对于求解多目标优化问题的Pareto最优解，目前已有多种基于遗传算法的求解方法。常用方法有:权重系数变换法、并列选择法、排列选择法、共享函数法及混合法等。本文采用权重系数变换法来实现多目标遗传算法求解，优化设计变量选定为内外径比值λ、外直径Do、气隙磁通密度Bg和气隙长度g。优化目标函数表述为

式中:Pden——功率密度;

η——电机效率;

Mmat——有效材料成本。Mmat由定转子铁心、线圈铜线以及永磁材料成本构成，硅钢片、铜线、钕铁硼永磁体价格分别按7.5 元/kg、70 元/kg、350 元/kg计算。

2.3 约束条件

轴向永磁电机的某些参数因受到材料本质特性或者应用环境的限制，其变化有一定的区间范围，作为优化设计的约束条件加以考虑。此外，优化设计变量本身也受到电磁和机械性能的约束限制，应当在其合理的变化区间内取值。轴向永磁电机的约束条件和设计要求，如表1所示。

表1 轴向永磁电机约束条件和设计要求

2.4 染色体编码

基本遗传算法采用二进制编码方式表示种群中的个体。其等位基因由0、1共同组成。初始种群的各个个体基因可由随机分布的数来生成，优化过程不依赖于优化变量初始值的选取。种群的大小选取为1 000，采用线性变换法调整适应度之间的差距，保持种群的多样性。

2.5 交叉和变异

在生物的遗传和自然进化过程中，两个同源染色体通过交配而重组，形成新的染色体，从而产生新的个体。遗传算法中，交叉操作把两个父个体部分基因加以替换重组形成两个新的子个体。通过定义的交叉概率，确定参与交叉操作的个体数，随机选取参与交叉的个体。交叉操作常采用单点交叉法、多点交叉法、均匀交叉法和算术交叉法等。本文交叉操作采用两点交叉法，其运算示意图如图4所示。

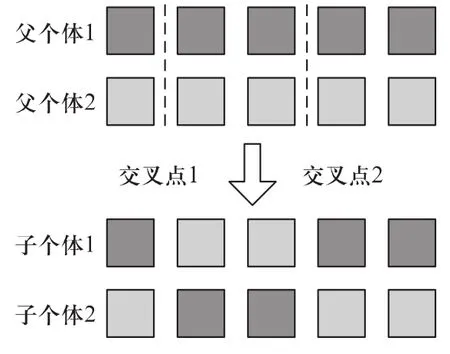
图4 两点交叉运算示意图

在生物的遗传和自然进化过程中，细胞分裂受到某些偶然因素的影响产生复制偏差，引起某些基因发生突变，产生新的染色体，表现出新的性状。遗传算法模仿生物遗传和自然进化中的变异环节，以较小的概率对编码串上的某些位进行改变，对于二进制编码就是0、1之间的变换。变异本身是一种随机的算法，能够弥补选择和交叉运算造成的某些信息的缺损，改善遗传算法的全局搜索能力，维持种群的多样性，防止出现早熟现象。变异操作常采用基本位变异、均匀变异、非均匀变异等方法。本文通过基本位变异实现遗传算法进化过程中变异操作，个体变异概率设定为0.05。

2.6 优化结果

通过遗传算法对10极12槽1.5 kW定子无磁轭模块化轴向永磁电机进行多目标优化设计，设定不同的权重系数，在满足额定技术要求的前提下，实现电机体积小、功率密度大、效率高、经济性好的优化设计目标。5组不同权重系数下以功率密度、效率、材料成本为目标函数的遗传算法优化设计结果，如表2所示。

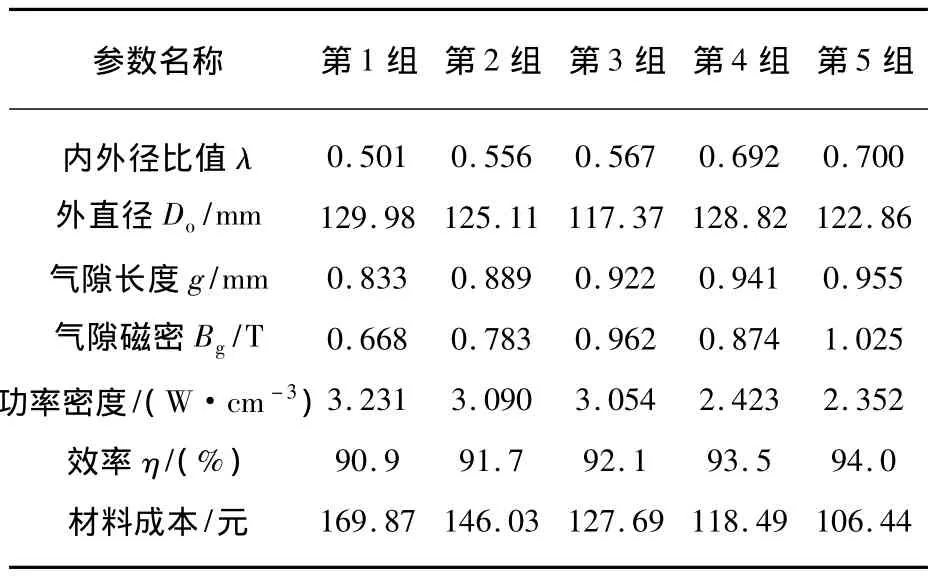
表2 轴向永磁电机优化设计结果

从表2可看出，诸多优化目标函数之间并不呈现单一的耦合关系，实际工程应用过程中会涉及到各优化目标间的协调和折中，按照实际的设计需求，可通过选取不同的权重系数来实现满足特定要求的最优设计。为了便于分析，采用插值得到电机功率密度、效率随外直径、内外径比值变化的曲面，分别如图5、图6所示。

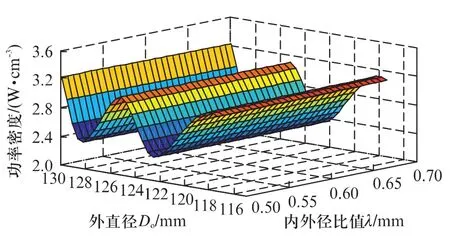
图5 功率密度随外直径和内外径比值变化曲面

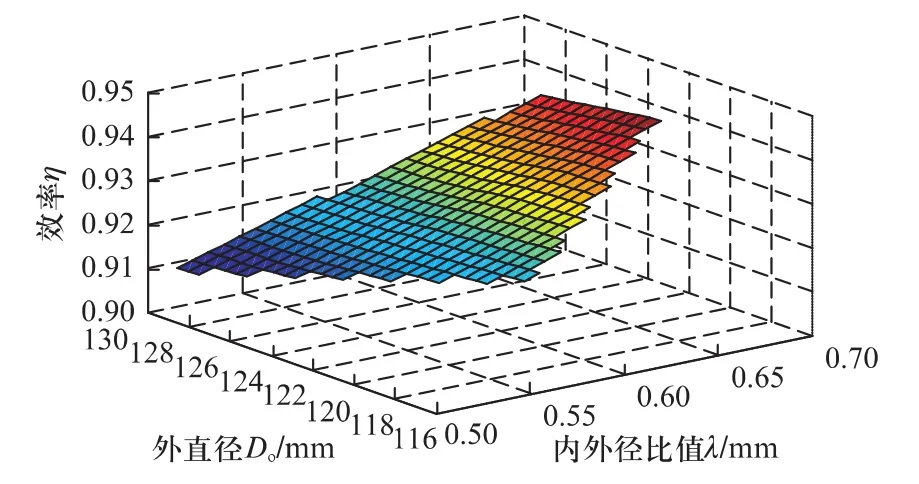
图6 效率随外直径和内外径比值变化曲面

由图5可知，外直径Do和内外径比值λ变化对功率密度影响呈现波动状态，存在多峰值和非单一的映射关系，而遗传算法能够通过有限的迭代在全局范围内寻找最优解。由图6可知，效率有随外直径和内外径比值增大而增大的趋势，但增长速率逐渐减慢。

3 有限元分析

轴向永磁电机特殊的结构形式，使得磁通密度沿径向和轴向的分布体现“弯曲效应”和“边缘效应”两个独立的3D效应。三维有限元分析同时考虑两种效应的影响，能够获得精确度较高的电磁场分析结果。

本文选取表2中第3组数据进行定子无磁轭模块化轴向永磁电机电磁设计，优化后的功率密度和效率分别为3.054 W/cm3和92.1%。轴向永磁电机的主要参数如表3所示。

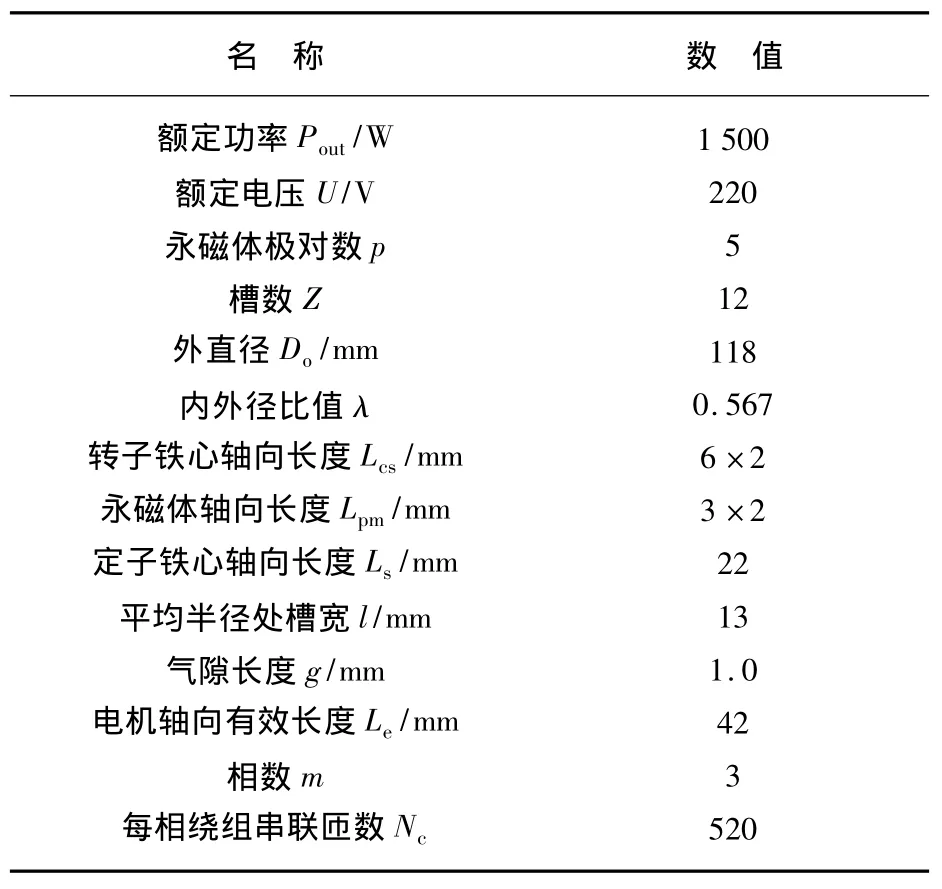
表3 轴向永磁电机的主要参数

为了验证遗传算法优化设计的有效性，利用JMAG软件建立该电机的三维有限元模型，进行有限元仿真分析。有限元法分析轴向永磁电机磁密分布如图7所示，定转子铁心处磁密均值约1.3 T。平均半径处气隙磁通密度波形图如图8所示，气隙磁密最大值为0.998 T，均值达0.47 T，和遗传算法优化结果相吻合，误差仅为3.74%。

由于永磁体和定子齿槽之间的相互作用，永磁电机不可避免产生齿槽转矩，引起转矩波动，带来振动和噪声，影响系统的控制精度。在高性能的永磁电机设计中，齿槽转矩抑制必须予以重视。针对轴向永磁电机，从转子结构考虑，改变永磁磁极参数的齿槽转矩抑制方法主要有永磁体斜极、极弧系数优化、永磁磁极偏移、永磁体极距调整等[10-15]。对于表贴式轴向永磁电机，改变永磁体结构形式较易实现。本文采用永磁体偏移的方法来抑制齿槽转矩，偏移的机械角度为4°。永磁体偏移4°分布图如图9所示。偏移前后齿槽转矩波形的对比如图10所示。通过计算，永磁体偏移后，齿槽转矩减小了70.6%，实现了齿槽转矩的有效抑制。

图7 轴向永磁电机磁密分布

图8 平均半径处气隙磁通密度波形图

图9 永磁体偏移4°分布示意图

图10 偏移前后齿槽转矩波形的对比

轴向永磁电机在3 000 r/min时的反电动势波形如图11所示。由图11可知相反电动势有效值为220.18 V。对反电动势进行傅里叶分析，其谐波分量如图12所示。由图12可知反电动势谐波含量较少，波形具有较高的正弦度。

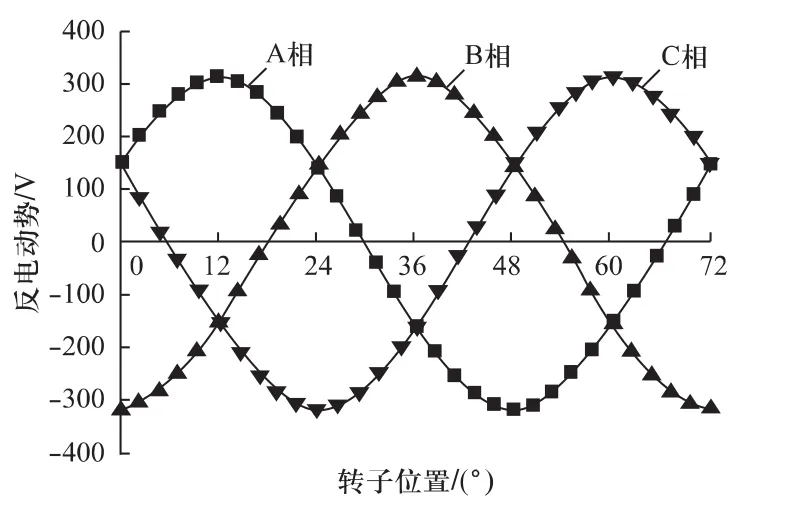
图11 反电动势波形

图12 反电动势谐波分量

效率是电机的一个重要性能指标，其取决于运行时电机中所产生的损耗，包括定子和转子铁心中的基本铁耗、绕组铜耗和附加杂散损耗等。通过有限元分析可准确计算出电机各部分损耗，进而求得功率密度和效率。比较有限元分析和遗传算法的优化设计结果，两者基本一致，结果对比如表4所示。

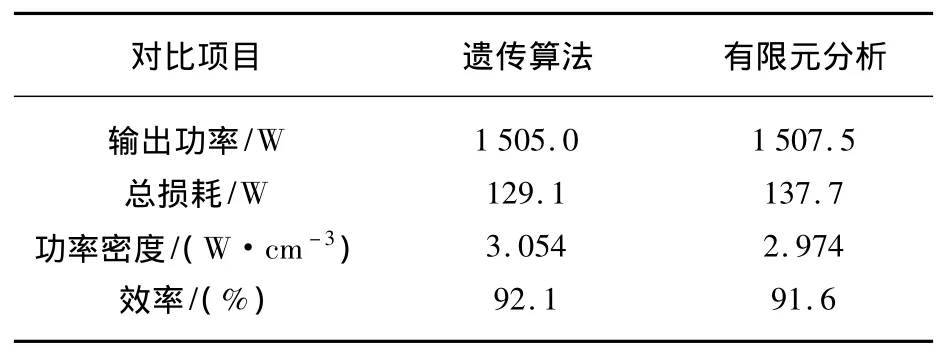
表4 有限元分析和遗传算法优化结果对比

4 结语

本文采用遗传算法和有限元分析，对定子无磁轭模块化轴向永磁电机进行了优化设计，以功率密度、效率、经济性为优化目标，在满足电机技术要求的前提下，实现多目标函数的最优寻解。三维有限元的分析结果验证了遗传算法优化设计的有效性。本文所采用的方法适用于各种结构的轴向永磁电机的优化设计，对于其他类型电机的优化分析也有一定的参考价值。

定子无磁轭模块化轴向永磁电机优化设计具有以下特点:

(1)轴向永磁电机的优化设计是一个非线性、有约束、多变量、多维度的复杂工程问题，而遗传算法具备良好的全局寻优能力，适合应用于该类电机的优化设计。

(2)采用遗传算法可以实现多目标函数的最优寻解，考虑各个优化目标之间的协调和折中，通过选取不同的权重系数来实现满足特定需求的最优设计。

(3)遗传算法优化设计的有效性通过三维有限元分析得以验证，且优化过程充分考虑了电磁和机械性能对优化变量的约束限定。

(4)由于永磁体和定子齿槽之间的相互作用，永磁电机不可避免地产生齿槽转矩，引起转矩波动，通过采取永磁体偏移的方法来抑制齿槽转矩，反电动势谐波含量较少。

[1]GIERAS J F，WANG R J，KAMPER M.Axial flux permanent magnet brushless machines[M].New York:Springer Verlag，2008.

[2]CAPPONI F G，DONATO G D，CARICCHI F.Recentadvances in axial-flux permanent-magnet machine technology[J].IEEE Transactionson Industry Applications，2012，48(6):2190-2205.

[3]范镇南，韩力.电机优化设计技术发展情况[J].电机与控制应用，2006，33(8):3-7.

[4]MAHMOUDI A，KAHOURZADE S，RAHIM N A，et al.Design，analysis，and prototyping of an axialflux permanent magnet motor based on genetic algorithm and finite-element analysis[J].IEEE Transactions On Magnetics，2013，49(4):1479-1492.

[5]YOUSEFI B，SHIRAZI A N，SOLEYMANI S，et al.Genetic algorithm application for optimum design of three phases disk type PM motor[J].International Journal on Computational Sciences and Applications，2012，2(6):1-7.

[6]ROSTAMI N，FEYZI M R，PYRHONEN J，et al.Genetic algorithm approach for improved design of a variable speed axial flux permanent magnent synchronous generator[J].IEEE Transactions on Magnetics，2012，48(12):4860-4865.

[7]GHOLAMIAN S A，ARDEBILI M，ABBASZADEH K，et al.Optimum design of slotted axial flux internal stator motorusing geneticalgorithm forelectric vehicle[J].International Journal of Software Engineering and Applications，2011，2(3):79-93.

[8]CHUNAYD，KOOADH，CHOBYH.Multiobjective optimization design ofaxialflux permanent magnet motor[J].International Journal of Applied Electromagnetics and Mechanics，2007，25(1):613-619.

[9]HUANG S，LUO J，LEONARDI F，et al.A comparison of power density for axial flux machines based on the general purpose sizing equation[J].IEEE Transactions on Energy Conversion，1999，14(2):185-192.

[10]杨玉波，王秀和，张鑫，等.磁极偏移削弱永磁电机齿槽转矩方法[J].电工技术学报，2006，21(10):22-25.

[11]AYDIN M，ZHU Z Q，LIPO T A.Minimization of cogging torque in axial-flux permanent-magnet machines:design concepts[J].IEEE Transactions on Magnetics，2007，43(9):3614-3622.

[12]杨玉波，王秀和，丁婷婷，等.极弧系数组合优化的永磁电机齿槽转矩削弱方法[J].中国电机工程学报，2007，27(6):7-11.

[13]GULEC W M，METIN A.Influence of magnet grouping in reduction of cogging torque for a slotted double-rotor axial-flux PM motor[C]∥International Symposium on Power Electronics，Electrical Drives，Automation and Motion，2012:812-817.

[14]JONG H C，JUNG H K，DONG H K，et al.Design and parametric analysis of axial flux PM motors with minimized cogging torque[J].IEEE Transactions on Magnetics，2009，45(6):2855-2858.

[15]GULEC M，AYDIN M.Reduction of cogging torque in double-rotor axial flux permanent magnet disc motors:a review of cost effective magnet skewing techniques with experimental verification[J].IEEE Transactions on Industrial Electronics，2013(99):1-9.