基于流方的笼型异步电机转子故障诊断

王 臻， 李 承， 王 蕾

(华中科技大学 电气与电子工程学院，湖北 武汉 430074)

0 引 言

三相交流异步电动机是应用最广泛的电气设备之一，其用电量占整个电力系统总用电量的60%以上。对电机进行必要的早期监测，提前发现故障征兆，及时采取有效措施，对降低事故的发生率和严重程度具有重要意义。故障早期信号微弱、运行环境变化、负载波动都会增大信号检测的困难。因此，采取有效实用的方法及时识别电机故障是必要的。目前,基于定子信号检测的电机故障诊断是应用最广泛的方法，具体包括快速傅里叶变换(Fast Fourier Transform, FFT)、频域分析[1]、Park矢量法[2，3]、小波变换[4]、基于人工智能[5]的电机故障诊断方法。

根据频谱特点的变化辨识电机故障是较早研究信号处理的方法。当电机发生断条故障时，在电机定子绕组的电流频谱中产生(1±2ks)f1的故障特征量，故以此故障特征频率作为异步电机转子断条的诊断依据。因为转差率在额定运行时通常很小，故障频率(1±2ks)f1很容易被基波频率f1淹没，所以直接对采集的定子电流直接做快速傅里叶变换效果不好，易产生误差和误断。利用连续细化的傅里叶变换分析方法，可获得采样原信号中某一主频率分量的精确分析表达式，即精确的幅值、频率、初相位等信息，从而避免故障频率易被淹没的问题[6]。

另一种改进方法，是对采集的定子电流信号进行计算处理，使故障频率(1±2ks)f1转化并放大为更易检测和分离的其他特征故障频率[7-9]。文献[10]通过采集的定子电压和电流乘积得到的单相瞬时功率，提取出转子断条故障时瞬时功率故障频率2ksf1、(2±2ks)f1，以故障频率2ksf1为断条故障特征频率可有效诊断转子断条故障。文献[11]在三相平均瞬时功率中提取故障频率2ksf1，由于三相平均瞬时功率只含有惟一特征频率2ksf1，故其特征频率幅值更集中，检测效果更好。文献[12，13]利用两相坐标系中瞬时无功功率的概念，在定子瞬时无功功率中提取转子断条特征故障频率2ksf1，从而取得和三相瞬时功率故障诊断相当的效果。本文根据瞬时功率的启示，提出了流方的概念和基于流方的故障诊断方法，提取转子断条故障特征频率2ksf1、转子偏心故障频率mfr，对比瞬时功率的诊断方法，其无须采集定子电压，只须检测定子电流，硬件开销更小，接线更简单，更利于在线故障诊断。

1 基于单相流方的转子断条故障诊断

1.1 基于单相流方的转子断条故障特征频率的提取

转子断条故障边频分量(1±2ks)f1易被基频f1淹没，且故障发生的初始阶段故障信号偏弱，故直接对电机定子电流频谱分析很难提取故障特征信号。为了放大故障频率信号以及把故障信号和基频分离出来，通过研究发现，电机定子电流自平方后，可以放大和转移特征故障频率。

类比瞬时功率，定义一个新的物理量“流方”，其表示n个故障电流自相乘，用字母q表示，则单相流方表示为

q(t)=i(t)n

(1)

首先，讨论n=2无故障状态下，电机的单相定子流方为

(2)

此量包含一个恒定直流分量和一个频率为2f1分量。

发生故障时，定子三相电流可表示为

2ks)2πf1t-φωp1]+Iωn1cos[(1-

2ks)2πf1t-φωn1]

(3)

式中：Iωp1、φωp1——故障频率(1+2ks)f1的幅值、初相位；

Iωn1、φωn1——故障频率(1-2ks)f1的幅值、初相位。

由算式(1)得断条故障时的单相流方为

q(t)= {I1cos(ω1t-φ)+Iωp1cos[(1+

2ks)ω1t-φωp1]+Iωn1cos[(1-

2ks)ω1t-φωn1]}2

(4)

式(4)化简并同频率合并后为

q(t)=q0(t)cosφ0+q2(t)cos(2ωt+φ2)+

q2±2s(t)cos[(2±2ks)ωt+φ2±2s]+

q2±4s(t)cos[(2±4ks)ωt+φ2±4s]+

q2s(t)cos(2ksωt+φ2s)

(5)

式中：q0(t)、φ0——频率为0的单相流方的幅值、初始相位；

q2(t)、φ2——频率为2f1的单相流方的幅值、初始相位；

q(2±2s)(t)、φ2±2s——频率为(2±2s)f1的单相流方的幅值、初始相位；

q(2±4s)(t)、φ2±4s——频率为(2±4s)f1的单相流方的幅值、初始相位；

q2s(t)、φ2s——频率为2sf1的单相流方的幅值、初始相位。

由式(5)可看出，转子断条故障时流方项既含无故障时的直流分量和2f1分量，也包括了分别为(2±4ks)f1、(2±2ks)f1、2ksf1、4ksf1的断条故障频率分量。为避免特征故障频率被淹没，可选特征故障频率为2ksf1(k=1时的故障分量最大)。

1.2 基于单相流方的转子断条故障诊断试验

本文试验采用的异步电机型号为Y132M- 4，额定功率7.5kW，额定电压380V，额定电流15.4A，额定转速1440r/min，采样频率5000Hz，采样点数20056。为信号分析的准确性，进行FFT频谱分析时，采用的数据量应当是2的整数次方，故采用数据量为16384。无故障状态和3根转子断条时的单相流方频谱分别如图1(a)、图1(b)所示。

图1 两种状态下的单相流方频谱

通过对比图1可得结论：

(1) 故障信号经平方后被显著放大，且故障频率由(1±2ks)f1变为2ksf1，可有效避免被基频淹没；

(2) 通过单相定子电流自乘方，然后依据流方频谱，提取特征频率2sf1，可有效辨识电机断条故障。

与基于瞬时功率的故障诊断技术相比，基于流方的电机故障诊断技术在工程应用阶段只须检测电机的定子电流数据，而无须采集定子电压，硬件开销小，连接更简单，在线诊断更方便。

2 基于三相总流方的转子断条和偏心故障诊断

2.1 基于三相总流方的转子断条故障频率的提取

由于异步电机的对称性，在推导三相总瞬时功率时发现，三相总瞬时功率的表达式更简单。由于故障频率的惟一性，故障频率更加集中，考虑提取基于三相总流方的故障信号，三相总流方定义为

(6)

电机无故障状态下的总流方为

(7)

即无故障状态下电机定子三相总流方是单一的直流分量。

当电机转子发生断条故障时，为求总流方把式(3)带入式(6)，化简可得

I1Iωp1cos(2ksω1t+φ-φωp1)+

I1Iωn1cos(2ksω1t-φ+φωn1)+

Iωp1Iωn1cos(4ksω1t+φωn1-φωp1)]

(8)

同频率合并可得

q(t)=q0(t)cosφ0+q2s(t)cos(2ksωt+φ2s)+

q4s(t)cos(4ksωt+φ4s)

(9)

可知，故障流方频谱中既包含直流分量，又包含定子电流边频分量引起的故障分量2ksf1、4ksf1，即(1±2ks)f1→2ksf1,4ksf1。

2.2 基于三相总流方的转子偏心故障频率的提取

当感应电机的转子发生偏心故障时，定子电流中会产生故障成分，为

fecc=(f1±mfr)

(10)

式中：m=1,2,3…；

f1——外加电源频率；

fr——电机转子旋转频率。

当转子出现偏心故障时，定子各相电流可表示为

φecnm]}

(11)

把式(11)代入式(6)，可得偏心故障下的总流方为

I1Iecpmcos(kωrt+φ-φecpm)+

I1Iecnmcos(kωrt+φ-φecnm)+

IecpmIecnmcos(2kωrt+φecnm-φecpm)]

(12)

同频率合并，可表示为

q(t)=q0(t)cosφ0+qmwr(t)cos(mwrt+

φ-φmwr)+q2mwr(t)cos(2mwrt+

φ-φ2mwr)

(13)

式中：Iecpm、φecpm——频率为(f1+mfr)的幅值、初相位；

Iecnm、φecnm——频率为(f1-mfr)的幅值、初相位。

同样，由式(13)可知故障流方频谱既包含直流分量，又包含定子电流故障分量引起的总流方故障分量mfr、2mfr，即(f1±mfr)→mfr,2mfr。

2.3 断条故障试验

无故障状态下和转子断条故障下，三相总流方的频谱图分别如图2(a)、图2(b)所示。其中，单电机无故障时主要包含直流分量，而3根断条时，则包含了故障频率2ksf1、4ksf1。因此，可得结论：

(1) 基于三相总流方的断条故障可提取特征故障频率分量2sf1，以此识别转子断条故障，有效放大故障信号，同时避免故障频率被基频淹没。

(2) 与单相流方技术相比，基于三相总流方的故障诊断方法，在有、无故障两种状态下的表达式更简洁，特征故障信号更集中，特征信号2sf1幅值更大，故辨识精度更高、诊断效果更好。

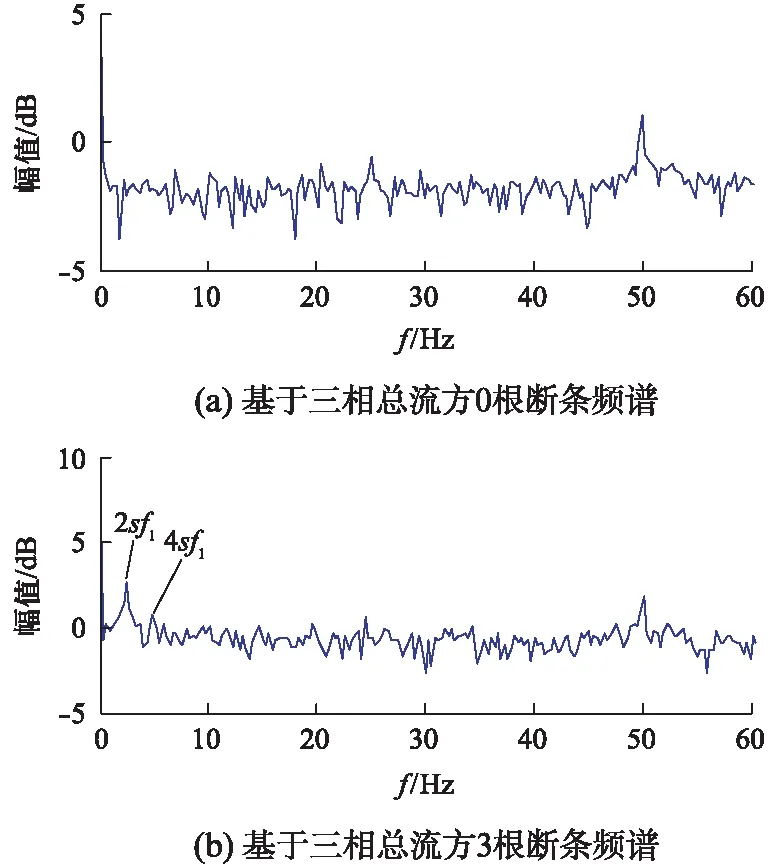
图2 两种状态下的三相总流方频谱图

2.4 偏心故障试验

转子偏心故障时定子电流频谱图和三相总流方频谱图分别如图3(a)、图3(b)所示。可得结论：

(1) 基于三相总流方的转子偏心故障可提取特征故障频率分量mfr，以此辨识转子偏心故障，故障分量幅值明显，故诊断效果较好。

(2) 定子电流中频率(f1±mfr)与三相总流方的故障分量mfr一一相对应。

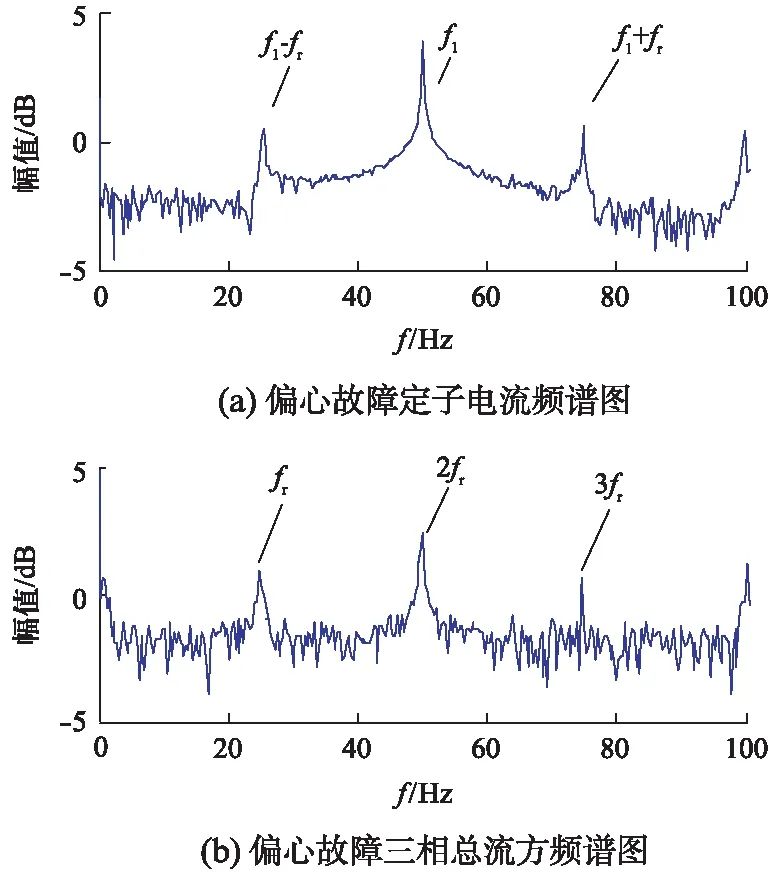
图3 偏心故障频谱

2.5 混合故障

复合故障的流方频谱图如图4所示。由图4可知，电机转子同时发生断条和偏心故障时，由于两种故障的特征故障频率2ksf1和mfr相距较远，用总流方的故障诊断方法可有效辨识转子断条和偏心的混合故障。

图4 复合故障的流方频谱图

3 关于流方参数n的讨论和选取

在上文关于流方的讨论中，为推导算式验证的方便，令n=2。已知定子电流的自乘方会使故障信号放大，且信号不易被基波淹没，易提取分离。但仍有以下两个问题值得讨论。

(1) 对于每个n≥2的取值，是否都能达到放大故障信号，且被放大的信号不易被淹没。

(2)n取值和故障信号的放大有何关系，n取何值时，诊断电机故障的效果更好。

分别令n=2～7，各自流方的频谱图分别如图5、图6所示。由图可知，当n取偶数时，其特征故障频率主要表现在2频率为2sf1表现都不明显，而集中于(2±2ks)f1。当n越大时，故障频率2sf1上的幅值越大，即针对此频率的检测越容易。缺点是此时的软件计算量加大。由于计算机技术的迅速发展，以及内存的快速扩充，计算量带来的软件开销问题越来越不明显，故可选择较大的偶数n值作为流方频谱故障诊断。sf1；当n取奇数时，其在

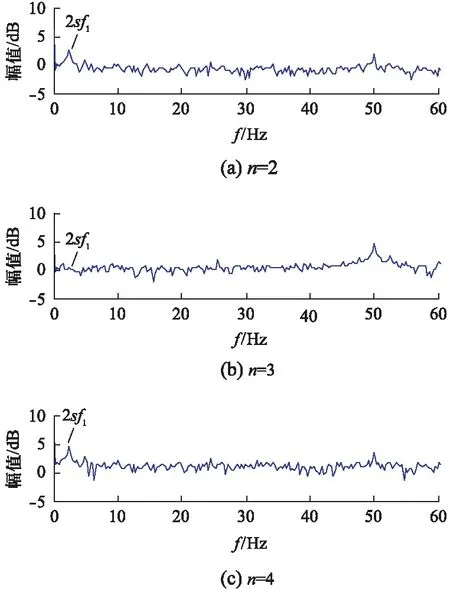
图5 n=2,3,4流方频谱

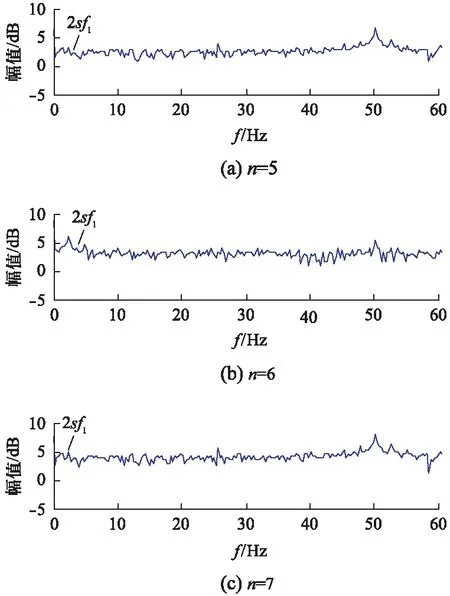
图6 n=5,6,7流方频谱

4 结 语

本文从自定义的流方概念出发，推导出了笼型异步电机转子断条和偏心故障在单相流方和三相总流方中的表现形式，提取出特征故障频率标识故障。算式和试验共同表明：

(1) 转子断条故障在单相流方中产生频率分量(2±2s)f1、2sf1，以频率2sf1作转子断条特征故障频率可诊断断条故障。

(2) 转子断条故障在三相总流方中产生频率2sf1的故障分量，相比单相流方法，其故障特征频率2sf1更集中，幅值更大，诊断效果更理想。

(3) 转子偏心故障在三相总流方中产生频率mfr的故障分量，利用三相总流方可有效辨识转子偏心故障。

(4) 对转子断条和偏心的复合故障，流方可分别提取出各自故障频率，有效辨识复合故障。

(5) 流方参数n必须选择偶数，n越大特征故障频率幅值越大，但随之增加了软件开销。

基于流方的电机故障诊断方法可有效避免故障频率被基频淹没的缺点。另外与瞬时功率故障诊断技术相比，只须采集定子电流而无须采集定子电压，信号采集更简单，更适合在线诊断。试验结果证明了上述结论。

【参考文献】

[1] 王金福，李富才.机械故障诊断的信号处理方法： 频域分析[J].噪声与振动控制，2013(1)： 173-180.

[2] 侯新国，吴正国，夏立,等.基于Park矢量模信号小波分解的感应电机轴承故障诊断方法[J].中国电机工程学报,2005,25(14)： 115-119.

[3] 方芳,杨士元，侯新国,等.派克矢量旋转变换在感应电机定子故障诊断中的应用[J].中国电机工程学报,2009,29(12)： 99-103.

[4] 罗忠辉,薛晓宁,王筱珍.小波变换及经验模式分解方法在电机轴承早期故障诊断中的应用[J].中国电机工程学报,2005,25(14)： 125-129.

[5] 刘冬生,赵辉,王红君.基于小波分析和神经网络的电机故障诊断方法研究[J].天津理工大学学报,2009,25(1)： 11-14.

[6] 张雄希,刘振兴.基于分数阶傅里叶变换的变频调速异步电机故障诊断方法[J].电机与控制应用,2007,37(4)： 59- 62.

[7] LEGOWSKI S F, SADRUL U A H M, TRZYNAD-LOWSKI A M. Instantaneous power as a medium for the signature analysis of induction motors[J]. IEEE Transactions on Energy Conversion， 1996，32(4)： 904-909.

[8] HACHEMI E, BENBOUZID M. A review of induction motors signature analysis as a medium for faults detection[J]. IEEE Transactions on Industrial Electronics， 2000，47(5)： 984-993.

[9] 侯新国，吴正国，夏立,等.瞬时功率分解算法在感应电机定子故障诊断中的[J].中国电机工程学报，2005,25(5)： 110-115.

[10] 刘振兴，张哲，伊项根.异步电机的状态监测与故障诊断技术综述[J].武汉科技大学报,2001,24(3)： 67-71.

[11] LIU Z, ZHANG X, YI X. Online rotor mixed fault diagnosis way based on spectrum analysis of average instantaneous power in squirrel cage induction motors[C]∥Proceedings of the 5th Word Congress on Intelligent Control and Automation, 2004： 1731-1735.

[12] DRIF M, CARDOSO A J M. The instantaneous reactive power approach for rotor cage fault diagnosis in induction motor drives[C]∥IEEE Power Eectrics Conference, 2008： 1548-1552.

[13] TOLBER L M, HABETLER T G. Comparison of time-based non-active power definitions for active filtering[C]∥IEEE Power Eectrics Congress, 2000： 73-79.