电力推进动态加载方法

王 森， 吴春秋

(海军驻上海江南造船(集团)有限责任公司军代表室，上海 201913)

0 引 言

在采用直流区域配电的电力推进船舶中[1]，推进系统的容量占船舶电网容量的 60%～70%。推进电机的起动过程伴随着巨大的能量需求，它带来的冲击给直流区域配电系统能否保持稳定的额定电压带来了巨大挑战。由于电磁过渡过程远大于机械过渡过程，推进电机作为发电机的负荷，负荷的电流增大，励磁电流来不及变化，必然导致发电机端电压降低，可能满足不了直流区域配电系统恒定电压的运行要求[2]。

经调研发现，现阶段电力推进船舶的起动过程由于没有一个定量的算法。为了安全起见，转速上升曲线设定比较平滑，在满足电力系统电压稳定性的基础上还有很大的余量能够提高加载速度[3]。

本文通过理论分析，得出了有效的控制方法使得船舶螺旋桨的转速能够在最短的时间上升到预定值，而供电系统直流输出端的电压跌落能够满足《钢质海船入级与建造规范》的相关要求。

1 电力推进系统

图1 电力推进系统

2 发电机平均数学模型

本文基于文献[5]构建了整流发电机模型。该模型将同步发电机和可控整流器作为一个整体来建模，构成了本文所研究对象的供电系统。该模型使用了同步发电机的超瞬变模型，并考虑了定子动态，三相同步电机的输出与整流器连接。

对于平均数学模型，在考虑定子绕组内阻的情况下，供电系统整流器的直流输出电压可以表示为[1]

(1)

其中，E为超瞬变电压幅值，可表示为

(2)

(3)

(5)

β为相对于发电机转子位置的整流器二极管触发角，Lc(β)与Lt(β)均为β的函数，表达式见文献[7]。

在供电系统与直流母线相连以后，考虑到直流母线上的滤波电路，同步发电机和可控整流器及直流母线系统简化模型如图2所示。

图2 同步发电机与可控整流器及直流母线系统简化模型

图2中，rs为定子绕组内阻，Lf、rf、C分别对应直流母线电感、电阻、电容。

3 推进负载及系统整体模型

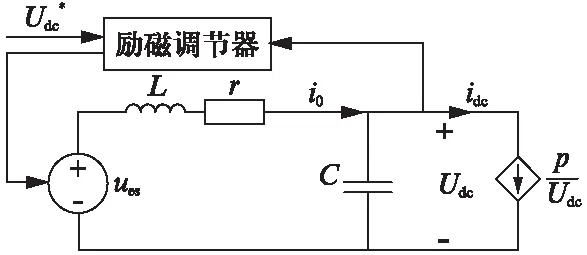
图3 电力推进系统简化电路模型

图4 发电机励磁调节器原理图

励磁调节器将直流母线的电压反馈至输入端，经PI调节输出励磁电压ufd，在励磁调节器结构和发电机参数确定的情况下，励磁电压至发电机端电压有着固定的传递函数。为了分析方便，在适当的改变比例微分参数后可以等效地认为励磁系统的控制对象是发电机的端电压，从而大大简化分析过程，使其清晰明了。直流母线电压udc与ues之间关系式为

(6)

由电力推进系统简化电路模型构建电路状态方程并将其写成微分方程的形式如下：

(7)

(8)

(9)

联立以上三式，消去变量i0与ues，得到udc与idc之间的关系式为

(10)

4 求取最优化转速控制的方法

在电力推进系统中，推进电机转速即螺旋桨转速n是加载的控制对象。由文献[1]可知，idc可以由推进电机的转速n表示为

(11)

假设推进电机的转速按照固定的速度上升，其斜率为k，初始转速为n0，则n=kt+n0得到直流母线电压udc的微分方程为

(12)

(13)

(14)

(15)

在系统参数确定的情况下，将螺旋桨扭矩系数km由二阶切比雪夫多项式km=a11+a12J确定，则直流母线电压udc可通过解式(12)得出，且其中只有k与n0两个变量。

设由式(4)解得udc的结果为udc=f(k,n0,t)。

5 最优解的验证

对于式(12)，由于参数过多，其解udc=f(k,n0,t)的一般形式颇为复杂，在参数不定的情况下可能出现无解，因此对一个参数确定的系统应用上述方式求解其满足条件的k值，以验证该方法的实用性和正确性。

按照GJB 4000—2000对潜艇直流电力系统瞬态电压跌落的要求，设直流母线电压允许跌落的最大比率λ为0.07。某船用三相交流同步发电机的参数如下： 额定容量sN=71kVA， 额定线电压UN=400V，额定转速nN=1500r/min， 电枢电阻rs=0.025pu，漏抗Xls=0.02pu， 同步电抗Xd=2.8pu，Xq=0.5pu,超瞬变电抗Xq″≈Xd″=0.03pu。直流母线参数如下：Lf=3mH，rf=0.2Ω，C=1400μF，L=Lt(β)+Lf=3.434mH。

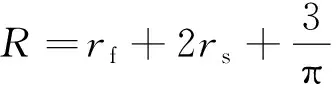
(16)

(17)

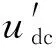
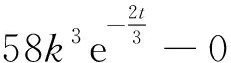
(18)

将以上结果做仿真验证，并构建其他两种仿真情况做对比。仿真一,Udc1的k值取上述分析得出的K=8.97；仿真二,Udc2中k值小于推导值，取k=5；仿真三，Udc3中k值大于推导值，取k=12。其仿真结果分别如图5所示。

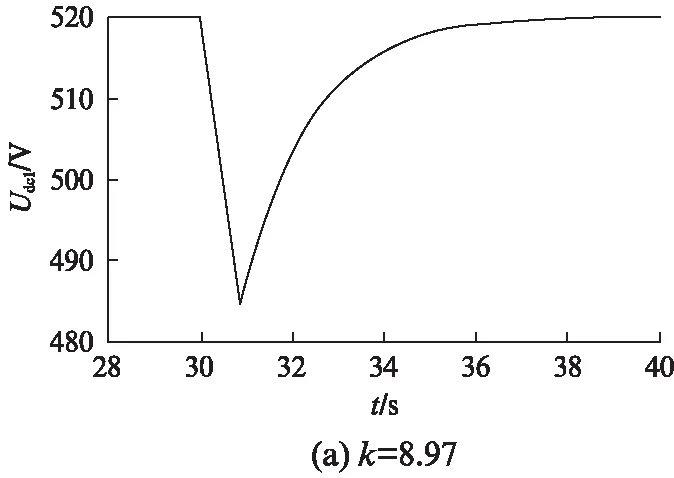
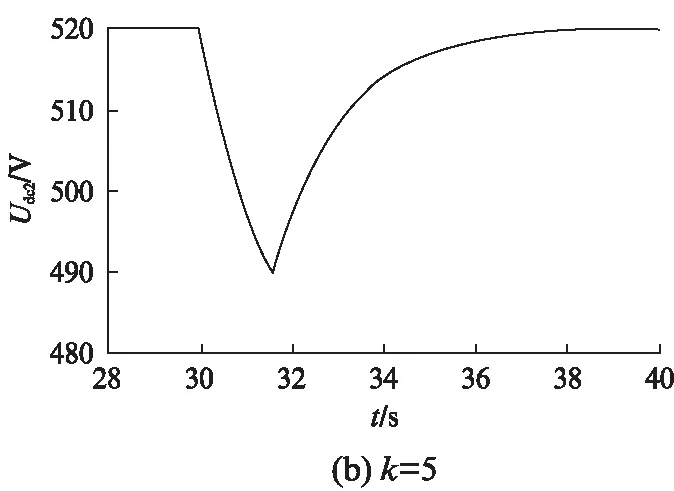
图5 k=8.97、k=5、k=12时直流母线电压变化曲线

仿真一结果显示，当推进电机转速在第30s时由2rad/s增加为10rad/s时电压跌落，电压跌落的时间正好为t=(10-2)/8.97=0.89s，与理论推导相同。

在励磁调节器的作用下，电压逐渐恢复到之前的520V，跌落最低至484.4V，满足电压跌落最低要大于520×0.93=483.6V的要求。但是仍然有484.4-483.6=0.8V的余量可以供其跌落，因而距离最优的电压降还有一定差距。也就是说转速n的增大速度还可以加大一点。这种误差主要是由于在K的推导计算过程中有简化的情况，在利用式(12)计算直流电压表达式时，为便于计算其结果中忽略了在t变化不大时数值较

小的项，从而造成结果误差。此外，推导过程中也未考虑同步发电机原动机的机械调节过程，同样造成了误差。

仿真二电压跌落至489.7V，离最低电压要求483.6V还有一定的距离，且加载时t=(10-2)/5=1.6s间因而不是最优控制；仿真三电压跌落至479.5V，尽管加载时间t=(10-2)/12=0.67s 小于前两种情况，但是不符合最低电压要求，电力推进系统可能存在危险。以上结果证明了该方法的使用有效性。

6 结 语

本文利用同步发电机的平均数学模型，将发电机与整流系统看做一个整体，作为系统的供电系统；再将推进电机和螺旋桨作为一个整体，等效为一个受控电流源，同时加载到供电系统输出端。在理论分析的基础上提出的加载方法使得推进电机能够在最短的时间内加载且能够满足电力系统电压稳定性要求。仿真证明该方法正确、有效。

【参 考 文 献】

[1] SALEHI V, MIRAFZAL B, MOHAMMED O. Pulse-load effects on ship power system stability[J].IEEE，2010(5)： 36-38.

[2] ZHU WD, STEVE P, JURI J, et al. A model-in-the-loop interface to emulate source dynamics in a zonal DC distribution system[J]. IEEE Transactions on Power Electronics, 2005,20(2): 122-132.

[3] LI D P, WANG Z Y,CHI H H. Chebyshev fitting way and error analysis for propeller atlas four quadrants[J].Journal of marine science and application, 2002,1(1)： 52-59.

[4] GAO H B. Modeling and simulation for marine electrical propulsion system [D]. Wuhan： Wuhan University of Technology, 2008.

[5] 范学鑫.舰船电力系统静态稳定性分析[D].武汉： 海军工程大学，2010.