基于高频旋转电压信号注入的IPMSM无位置传感器控制

寿利宾, 袁登科

(同济大学 电气工程系，上海 201804)

0 引 言

永磁同步电机(Permanent Magnet Synchro-nous Motor, PMSM)由于高效率、高功率密度和更好的动态响应等优点在现代电力传动系统应用越来越广泛[1]。在高性能的PMSM控制系统中，转子位置信息至关重要。使用位置传感器可获得转子位置信息，但是却带来成本上升、可靠性降低、在某些场合无法安装等问题[2]。

传统的无传感器控制技术基于基频模型或者观测器方法在电机高速时能满足需求，但在低速时由于反电势很小而难以实现。此外，此类方法严重依赖电机参数，而电机参数在不同运行状态下会发生变化。如何检测电机在低速甚至是零速下的转子位置信息成为当今无位置传感器控制技术的研究热点[3]。

本文对内置式PMSM(Interior PMSM, IPMSM)结构进行了分析，详细分析了转子位置估算方法，搭建了MATLAB仿真模型，给出了估算结构。

1 高频信号注入无传感器控制原理

目前主要存在的高频信号注入方式如下： (1) 在静止两相α、β坐标系下注入旋转信号。(2) 在旋转d、q坐标下注入脉振信号。(3) 在旋转d、q坐标下注入旋转信号。本文采用第一种方法，在电机基波电压上叠加一个高频旋转电压信号uαβ。转子位置信息可以从高频响应电流分量中提取出来。

注入的高频电压载波信号如下：

(1)

式中：uh——uαβ的幅值；

ωh——uαβ的高频角频率。

电机在d、q坐标系下的磁链数学模型为

(2)

通过坐标变换变成两相静止坐标系，转子的磁极位置为

(3)

式中：θ——转子旋转凸极(d轴)与A轴(α轴)的夹角。

简化得定子磁链在α、β坐标系下的矢量方程为

(4)

式中：ψs——定子磁链；

is——定子电流；

Ls(θ)——同步电感。

Ls(θ)表示为

(5)

式中：

注入高频信号后，电机的阻抗变得很高，主要的阻抗体现在电感方面，因此定子电压可以近似表示为[4]

(6)

由式(6)可得高频电流响应为

(7)

将式(1)代入式(7)并化简可得

(8)

其中，ip，in两个量分别为

转换成矢量形式为

(9)

由式(9)可知高频响应电流包含正序分量(与注入电压同向旋转)和负序分量(与注入电压反向旋转)。负序分量包含转子磁极位置信息。因此，只要能够提取出高频负序电流的相位，就可以得到转子位置。

正序电流的旋转轨迹与负序电流的旋转轨迹共同作用会形成一个椭圆。静止两相α、β坐标系下，转子在不同位置上高频电流矢量轨迹如图1所示。由图1可知，转子位置确定后，椭圆的方向也就唯一确定了，故对高频电流进行合理解调就能获取转子位置信息[5]。

图1 α、β坐标下转子不同位置上高频电流矢量轨迹

2 高频载波的信号处理

定子电流中包含电机的基频电流、低频的谐波电流和PWM开关谐波电流，故需要经过一系列的信号处理过程来提取负序分量。

电机的基频电流、低频的谐波电流的频率都低于注入的高频旋转信号的频率，而PWM开关频率远高于给定值，所以可以通过常规的带通滤波器来滤出高频载波电流[6]。

(10)

使用低通滤波器将ipej2ωht滤除,滤波之后的信号就只含有位置信号inej2θ。将inej2θ在两相静止坐标系中用分量形式表示为

(11)

(12)

图2 负序电流提取过程

3 转子磁极位置估计误差解决方法

锁相环技术包含鉴相器、压控振荡器和环路滤波器。鉴相器用来鉴别输入信号与输出信号之间的相位差，并输出误差电压ud。ud中的噪声和干扰成分被低通性质的环路滤波器滤除，形成压控振荡器的控制电压uc。uc作用于压控振荡器使其输出振荡频率拉向环路输入信号频率，二者相等时环路被锁定,称为入锁[7]。维持锁定的直流控制电压

由鉴相器提供,故鉴相器的两个输入信号间留有一定的相位差。锁相环结构如图3所示。

图3 锁相环结构图

使用外差法进行位置误差估计,在锁相环中的鉴相器环节中实现。环路滤波器由一个PI调节环节实现的，压控振荡器环节是一个积分环节。转子位置观测器如图4所示。

图4 转子位置观测器

4 系统仿真及结果

为了验证本文研究的IPMSM无位置传感器控制算法的可行性，搭建如图5所示的MATLAB仿真模型。电流环和速度换都选用经典的比例-积分控制器，采用id=0的矢量控制[8-9]。带阻滤波器的作用是提取出矢量控制中反馈回去的id、iq电流。带通滤波器用来提取高频载波电流。位置跟踪观测器实现对转子的位置和速度估计。注入的旋转高频电压幅值为10V，频率为1000Hz。电机参数如表1所示。

图5 BLDCM无位置传感器控制算法仿真模型

参数值极对数4转子磁链/Wb0.0875定子电阻/Ω2.875转动惯量/(kg·m2)0.0008直轴电感/H3.5e-3交轴电感/H8.5e-3

转子静止时，高频响应电流负序分量在两相静止坐标系下的运动轨迹为一个逆时针旋转的圆；正序分量的运动轨迹则为一个椭圆。基于高频旋转电压注入的仿真检测结果如图6所示。图6给出转子初始位置在0°、45°、90°时载波电流轨迹。随着转子的旋转，载波电流轨迹便会形成一个圆环。

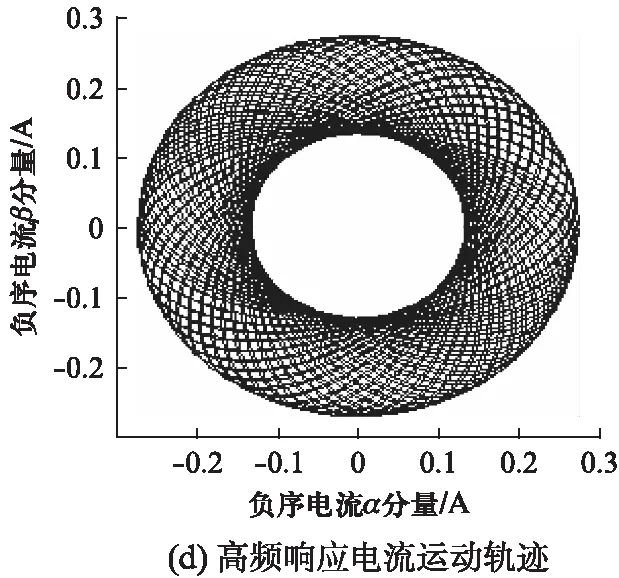
图6 基于高频旋转电压注入的仿真检测结果

给定转速250r/min时，转子位置估计、转速估计及转速误差如图7～图9所示。由图可知，估算所得的转子位置及转速都能很好地跟踪实际值。

图7 给定转速250r/min时的转子位置估计

图8 给定转速250r/min时的转速估计

图9 给定转速250r/min时的转子速度误差

图10～图12为给定转速变化时转子位置估计、转速估计和转速误差波形。由图可知，该方法具有较好的动态跟踪性能。

图10 给定转速变化时的转子位置估计

图11 给定转速变化时的转速估计

图12 给定转速变化时的转速误差

5 结 语

本文研究了一种BLDCM低速运行时的无位置传感器检测方法——高频旋转电压注入法。该方法使得电机在低速甚至零速时的可靠运行成为了可能。跟踪空间凸极位置法使这种无位置传感器方法对电机参数的变化不敏感，对外界的干扰具有很强的鲁棒性。仿真结果表明,该方法在低速及动态条件下均能够准确地观测出转子位置。

【参 考 文 献】

[1] TOSHIHIKO N. Trends of permanentmagnet synchr-onous machine drives[J]. IEEE Transactions on Electrical and Electronic Engineering, 2007, 2(2)： 125-142.

[2] 王高林,杨荣峰,李刚,等.基于高频信号注入的IPMSM无位置传感器控制策略[J].电工技术学报,2012,27(11)： 63-68.

[3] 吴奇,程小华.永磁同步电机的无传感器控制策略[J].电机与控制应用,2009,36(8)： 29-32.

[4] 王丽梅，郑建芬,郭庆鼎.基于载波注入的凸极永磁同步电动机无传感器控制[J].电机与控制学报，2005,9(4)： 334-336.

[5] 杜栩扬,胡育文,鲁文其,等.基于凸极跟踪的IPMSM转子初始位置自检测的研究[J].微电机,2010,43(10)： 55-59.

[6] 王高林,杨荣峰,于泳,等.内置式永磁同步电机无位置传感器控制[J].中国电机工程学报,2010,30(30)： 93-98.

[7] 刘毅.基于高频注入的永磁同步电机无位置传感器运行研究[D].杭州： 浙江大学,2005.

[8] 何继爱,王惠琴.永磁同步电机空间矢量控制系统的仿真[J].电力系统及其自动化学报,2005,17(6)： 15-16.

[9] 程启明,王映婓,胡晓青,等.基于SVPWM的永磁同步电机矢量控制系统的建模与仿真[J].上海电力学院学报,2012,28(4)： 330-335.