内嵌式永磁同步电机参数辨识技术

刘长柱， 张根发， 冯世军， 刘立恒, 夏义本

(1. 上海联孚新能源科技集团有限公司,上海 201201； 2. 上海大学 材料科学与工程学院，上海 200444)

0 引 言

永磁同步电机(Permanent Magnet Synchro-nous Motor, PMSM)具有效率高、体积小、重量轻等优点，被广泛应用于各个领域[1-2]。内嵌式PMSM(Interior PMSM, IPMSM)具有磁路不对称等特点，交直轴电感不同，具有较高的凸极率，可以有效利用磁阻转矩成分，提高PMSM的功率密度[3-6]。由于PMSM工作时温度变化、永磁体性能衰减等因素[8]，造成PMSM参数变化。为了提高PMSM的控制精确度，宋文祥等人研究了基于状态观测器的异步电机定子磁链观测和速度辨识[9]。该算法只针对异步电机进行参数辨识，无法直接应用于PMSM。Aydogmus等人采用扩展卡尔曼滤波对电机参数进行在线辨识[10]。该算法针对AC-AC逆变器控制的无速度传感器系统，算法相对复杂，需要进行大量的矩阵运算，不利于在DSP组成的嵌入式系统中实现在线辨识。Mobarakeh等人提出了基于解耦控制的PMSM在线参数辨识技术[11]。该算法辨识结果必须立即应用到系统控制中，辨识结果的误差对系统控制的精度影响较大，可能会造成系统不稳定。另有研究人员根据模型参考自适应理论提出了模型参考自适应参数在线辨识的方法[12-14]，但仅针对面装式的隐极PMSM。若自适应律选取不合理，极易导致系统不稳定。

本文首先采用离线辨识的方法，识别出PMSM参数，用于矢量控制的基本参数，实现PMSM的控制。因为PMSM参数受到温度、负载大小等影响，变化较大，所以又采用递推最小二乘法对IPMSM多参数进行在线同时辨识，并将辨识结果应用到PMSM矢量控制中，实现了最优控制。该方法可以同时辨识出IPMSM定子电阻、直轴电感、交轴电感、磁链等参数，具有方法简单和系统稳定性好等特点，可以有效提高电机的控制精度。

1 PMSM动态数学模型

忽略谐波、铁心饱和、铁耗、三相电流完全对称及转子无阻尼绕组的前提下，PMSMd、q轴坐标系下的稳态数学模型为[15-16]

(1)

式中：ud、uq——定子电压矢量的d轴、q轴分量；

id、iq——定子电流矢量的d轴、q轴分量；

Rs——定子电阻；

ψf——永磁体转子产生的磁链；

ωe——电动机电角速度；

Ld、Lq——电机定子绕组d、q轴电感。

2 PMSM参数的离线辨识方法

为实现PMSM的矢量控制，需对PMSM的参数进行离线辨识。

2.1 定子电阻的离线辨识

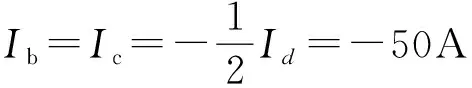
ud=Rsid

(2)

通过式(2)可以获得PMSM的定子电阻。通常情况下，对于大功率PMSM，定子电阻值较小。在实际控制过程中，可以忽略定子电阻。

2.2 磁链的离线辨识

采用Id=0的控制策略，控制电机以固定转速转动，则式(1)中第二式可简化为

uq=Rsiq+ωeψf

(3)

控制电机转速恒定，Rs通过定子电阻离线辨识的方法得到。因此，由式(3)可得PMSM的磁链ψf。

2.3 交直轴电感的离线辨识

类似于电机磁链辨识的方法,采用Id=0的控制策略，控制电机以固定转速转动，则式(1) 中第一式可简化为

(4)

同样，矢量控制时，采用Id≠0的控制策略，控制电机以固定转速转动，可得

(5)

上述离线参数辨识方法不能实时地对电机进行参数辨识。电机工作温度的变化、负载的大小等都会对参数产生影响。为能够准确地获得电机参数，需进行在线辨识。本文采用最小二乘法对电机参数进行在线辨识。

3 带遗忘因子的递推最小二乘法

最小二乘法是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。通常情况下，最小二乘法的系统模型为[17]

y(N)=φNTθ+ε(N)

(6)

式中：y(N)——系统输出序列；

φNT——系统输入序列；

θ——待辨识的参数序列；

ε(N)——修正项；

N——已获得观测数据的长度。

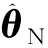
(7)

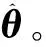
随着观测数据的不断增多，新观测值对参数估计的影响不断减小。最终，新数据的作用将被旧数据作用浸没，出现数据饱和，系统估计参数将不再跟踪系统真实参数变化，失去在线辨识的意义。因此，参数辨识需要将老数据逐渐遗忘，对新数据给予足够的重视。基于这种需求，本文引入了一个遗忘因子λ来解决由于“数据饱和”引起的估计参数不能追踪实时系统真实值的问题。遗忘因子λ一般选取0.950～0.999。遗忘因子越小，旧观测数据对系统估计参数的影响越小，新数据对系统估计参数的影响越大。

带遗忘因子的递推最小二乘法参数估计可以表示为[18]

(8)

K——增益矩阵；

P——协方差矩阵；

I——单位矩阵；

将d、q旋转坐标系下IPMSM的静态模型转化为最小二乘的标准格式。利用递推最小二乘法同时在线辨识出IPMSM定子电阻、直轴电感、交轴电感、磁链等多个参数。

4 IPMSM多参数在线辨识

将式(1)中需要辨识的Rs、Ld、Lq、ψf提取出来，改写成矩阵的形式如下：

(9)

对比式(6)与式(9)，可得

(10)

式(10)中，θ是需要辨识的参数矢量。将新观测到的数据不断迭代，可得IPMSM的Rs、Ld、Lq、ψf。

具体计算过程如下：

(2) 取P(N)为非常大的矩阵，例如P=104×I，I为单位矩阵。

(3) 根据式(8)计算增益矩阵K。

(4) 根据式(8)计算下一个协方差矩阵P(N+ 1)。

(5) 根据式(8)计算出需要辨识的参数θ。

通过循环迭代，最终θ将收敛在PMSM参数的真实值附近，实现PMSM参数辨识。

辨识过程中可能会出现结果的多值性问题。为此，在仿真过程中，人为的在电机转速的控制中加入低频小幅值的波动，从而获得电机不同运行点的数据，保证最小二乘法辨识结果的准确性。

5 系统仿真模型与仿真结果

为了验证方法的有效性，对150kW PMSM进行仿真[19-20]。

电机的参数如下： 额定功率150kW，额定转矩1100N·m，额定转速1300r/min，最高转速3000r/min，额定电压380V，定子电阻0.012Ω，直轴电感0.46mH，交轴电感1.35mH，磁链0.37Wb，极对数为4。

5.1 PMSM参数离线辨识仿真

5.1.1 定子电阻的离线辨识

由于150kW电机定子电阻较小，可以忽略。此次仿真没有对定子电阻进行离线辨识。

5.1.2 磁链的离线辨识

磁链的离线辨识采用Id=0的控制策略，控制PMSM以800r/min固定转速旋转。辨识结果如图1所示。为获得较为准确的磁链数值，将辨识结果导入MATLAB的工作空间，对输出的数据采用mean(simout.signals.values(500： end,1))函数求平均值，得到磁链平均值为0.3646Wb。

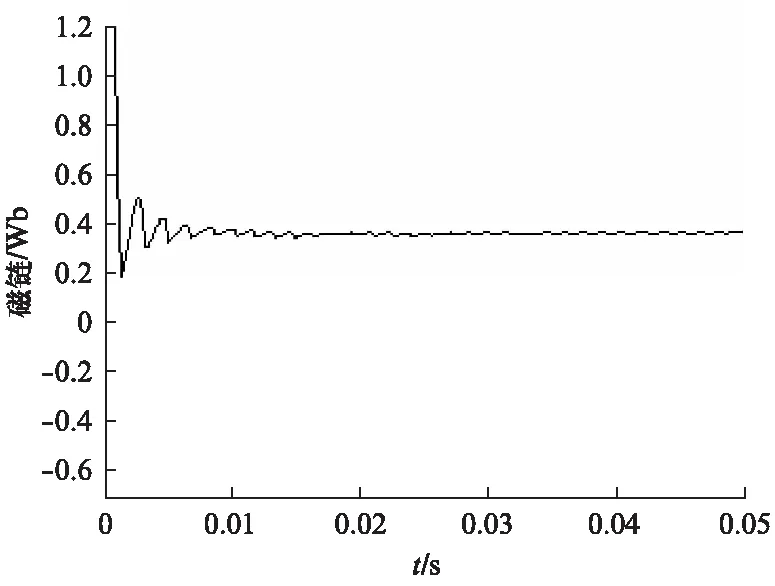
图1 磁链辨识结果

5.1.3 交轴电感的离线辨识

交轴电感的离线辨识采用Id=0的控制策略，控制PMSM以800r/min的固定转速旋转。辨识结果如图2所示。为获得较为准确的交轴电感数值，将辨识的结果导入MATLAB的工作空间，对输出的数据采用mean(simout.signals.values(500： end,1))函数求平均值，得到交轴电感平均值为1.3mH。

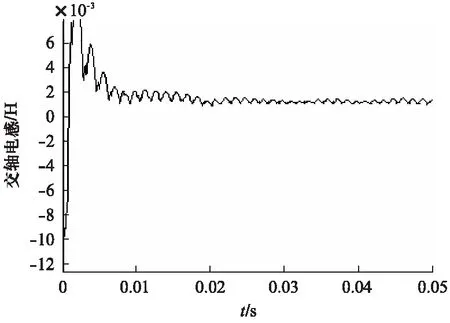
图2 交轴电感辨识结果

5.1.4 直轴电感的离线辨识

由式(5)可知，要对PMSM的直轴电感进行参数辨识，不能继续采用Id=0的控制策略。因此，设定Id的参考值为-10A，电机转速为800r/min。辨识结果如图3所示。

同样地，为获得较为准确的直轴电感数值，将辨识的结果导入MATLAB的工作空间，对输出的数据采用mean(simout.signals.values(500： end,1))函数求平均值，得到直轴电感平均值为0.45145mH。

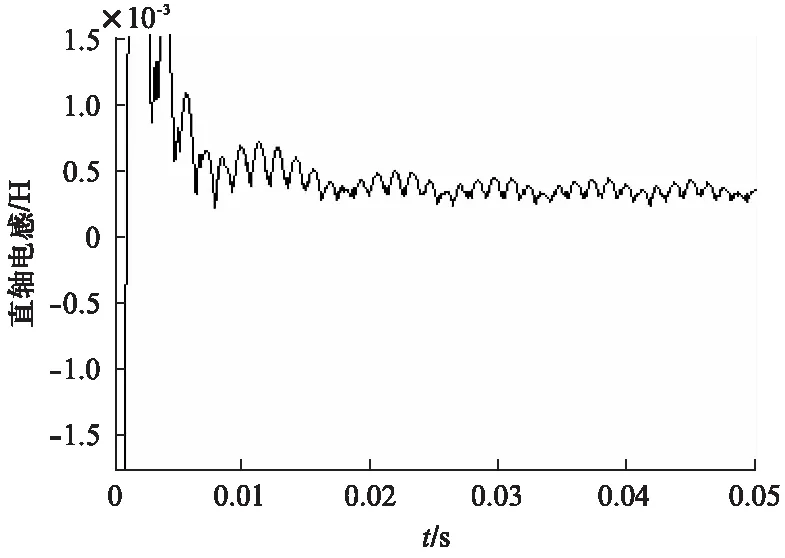
图3 直轴电感辨识结果

5.2 IPMSM参数在线辨识仿真

IPMSM参数辨识系统结构框图如图4所示。

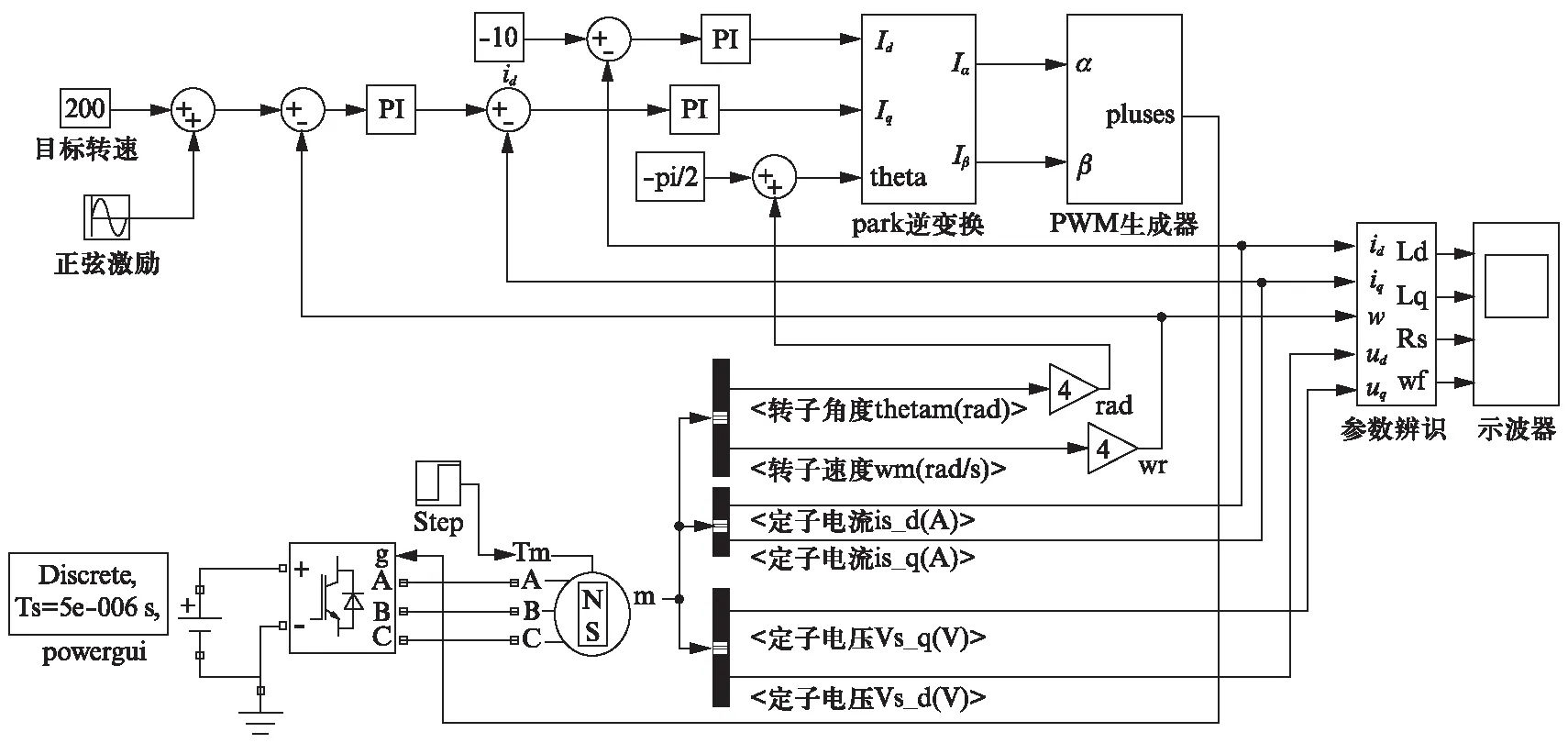
图4 IPMSM参数辨识系统结构框图

参数辨识模块(见图5)采用MATLAB下的S-Function 模块编写，参数辨识模块通过检测id，iq，ud，uq及ω循环迭代，实时更新，最终辨识出电机参数。Ld、Lq、Rs、ψf同时辨识后的结果如图6所示。图6(a)为直轴电感仿真波形，Ld最终收敛在真实值0.46mH附近。交轴电感仿真波形如图6(b)所示，Lq最终收敛在真实值1.35mH附近，定子电阻仿真波形如图6(c)所示，Rs最终收敛在真实值0.012Ω 附近，磁链仿真波形如图6(d)所示，ψf最终收敛在真实值0.37Wb附近。从图6可知，最终4个参数在0.15s的时间内稳定收敛在电机参数的真实值附近。

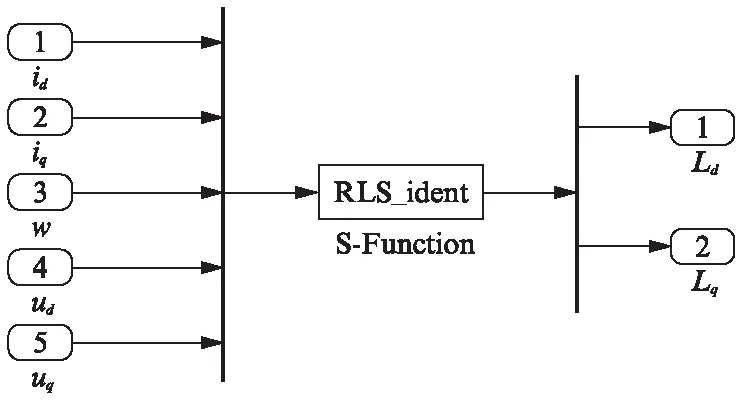
图5 参数辨识模块

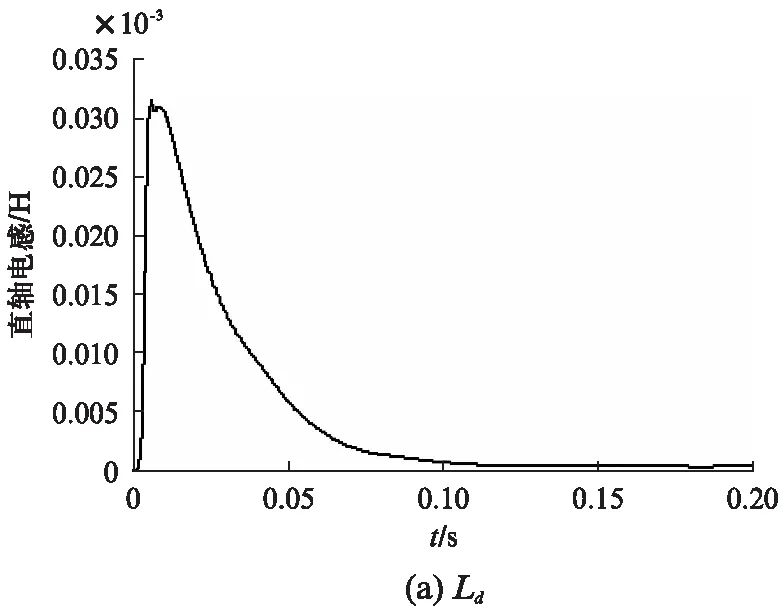
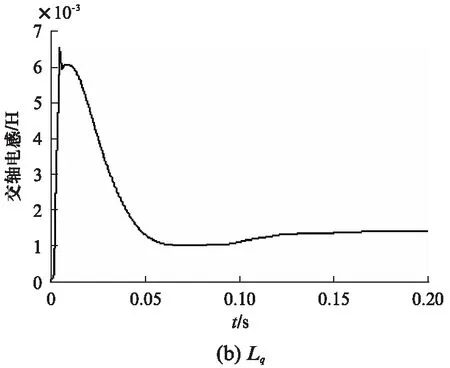
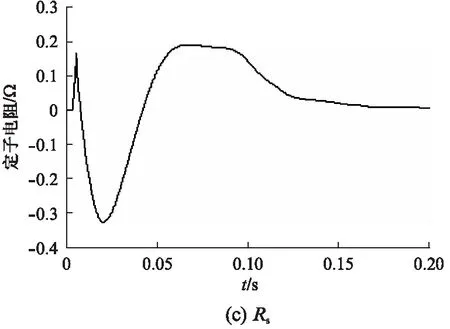
图6 辨识结果

为准确获得IPMSM的参数，将仿真得到的数据通过Simulink中的simout模块导入到MATLAB的工作空间，截取辨识参数稳定后的数据，并对其求平均值处理。与电机参数的真实值进行比较，得到辨识结果与真实值之间的误差。

为验证最小二乘法辨识参数的稳定性，在t=0.2s时添加一个阶跃信号，令负载转矩突增至80N·m，观察参数辨识结果，如图7所示。

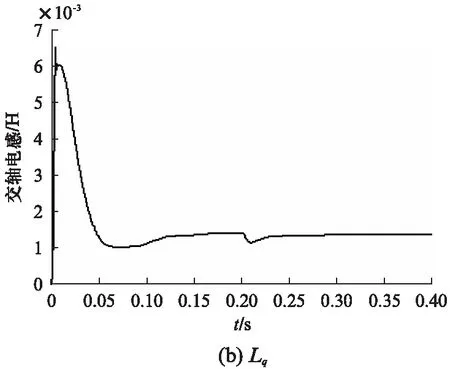
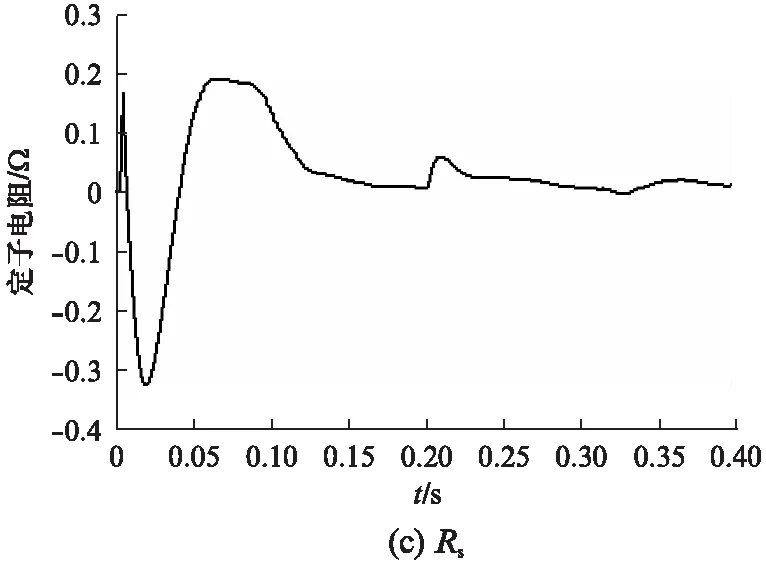
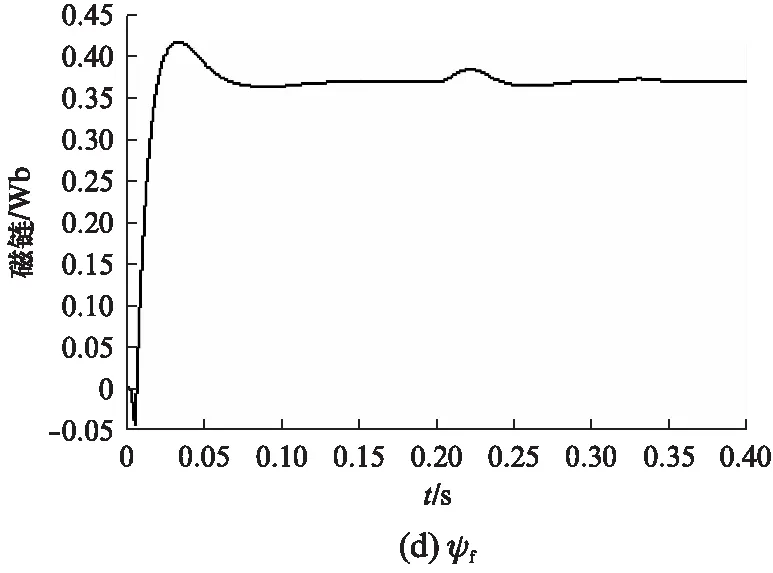
图7 辨识结果的阶跃响应

由图7可知，在t=0.2s时，扭矩突然增至80N·m，辨识结果突然变化，但在很短时间内又重新收敛到电机参数真实值附近。因此，采用遗忘因子的最小二乘法进行参数辨识是稳定可靠的。

5.3 仿真结果对比表

IPMSM参数离线辨识和在线辨识的辨识结果如表1所示。由表1可知，无论是采用离线辨识还是在线辨识，辨识参数与电机的实际参数之间的误差较小。因此，对于一台PMSM的矢量控制，可以先采用离线辨识的方法，初步得到电机的参数，并将该参数用于电机的矢量控制。然后，采用在线辨识的方式，实时辨识电机运行参数，以应对电机工作过程中由于温度变化、长时间运行等原因导致的参数漂移，提高矢量控制的稳定性。

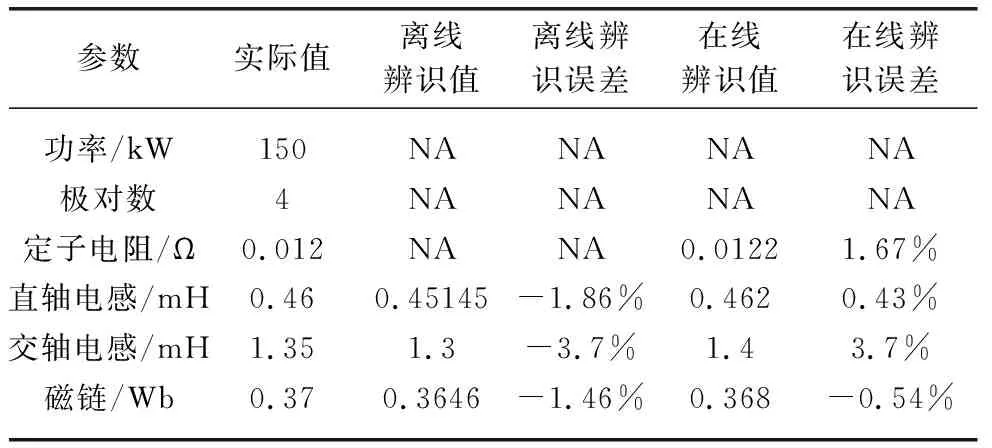
表1 IPMSM参数

6 结 语

PMSM参数离线辨识方法，可迅速得到电机的参数，且精度较高。IPMSM多参数在线辨识方法可在0.2s内收敛到电机参数的真实值附近，且具有误差小、精度高等优点。利用带遗忘因子的递推最小二乘法对IPMSM多参数进行在线辨识，可实时对PMSM参数进行校正，克服电机参数随环境变化、温度升高的影响而引起的较大范围的变动。该方法仅利用电机的直轴电流id、交轴电流iq、直轴电压ud、交轴电压uq及角速度ω，无须增加其他硬件设施，减少了外界干扰对PMSM参数辨识结果的影响，提高了参数辨识的可靠性与准确性。采用该方法可以对IPMSM多参数进行在线同时辨识，可以辨识出IPMSM定子电阻、直轴电感、交轴电感、磁链等参数，具有方法简单、辨识速度快、实时性强及系统稳定性好等优点，可以有效地提高IPMSM的控制精度。

【参 考 文 献】

[1] 郭秀英,赵伟民.永磁电机在抽油机中的应用[J].科技创新导报,2010(5)： 210.

[2] 许峻峰,冯江华.永磁同步传动系统的应用概况[J].大功率变流技术,2010(1)： 38- 43.

[3] 柯以诺.永磁同步电机传动系统在电动车辆上的应用[J].大功率变流技术,2009(5)： 31-37.

[4] 温旭辉.电动汽车电动机驱动技术及其发展[J].电气时代,2010(9)： 58-60.

[5] 王迪.基于矢量控制的纯电动汽车永磁同步电机驱动系统研究[D].哈尔滨： 哈尔滨理工大学,2010.

[6] 宗世勇.混合动力汽车永磁同步电机矢量控制的研究[D].长沙： 湖南大学,2010.

[7] 覃家财.内置式永磁同步电机电感参数对转矩的影响[D].重庆： 重庆大学,2012.

[8] 王艾萌,魏亮,李和明.考虑磁路交叉饱和的内置式永磁同步电动机调速控制[J].微特电机,2010(3)： 42- 45,49.

[9] 宋文祥,曹大鹏,陈国呈,等.基于状态观测器的异步电机定子磁链观测和速度辨识[J].上海大学学报自然科学版,2008,14(4)： 349-354.

[10] AYDOGMUS O, SÜNTER S. Implementation of EKF based sensorless drive system using vector controlled PMSM fed by a matrix converter[J]. International Journal of Electrical Power & Energy Systems, 2012,43(1)： 736-743.

[11] MOBARAKEH B N, FARID M T, SARGOS F M. On-line identification of PMSM electrical parameters based on decoupling control[C]∥Industry Applications Conference, Thirty-Sixth IAS Annual Meeting, Chicago, USA, 2001,1(1)： 266-273.

[12] FRENZEL B, KURZWEIL P, RÖNNEBECK H. Sensorless direct torque control of hybrid stepper motor based on MRAS[J]. Energy Procedia, 2012(14)： 1992-1997.

[13] 陈振锋,钟彦儒,李洁.嵌入式永磁同步电机自适应在线参数辨识[J].电机与控制学报, 2010,14(4)： 9-13.

[14] 赵克,安群涛,孙力.永磁同步电动机参数自适应辨识的建模与仿真[J].系统仿真学报,2009,21(12)： 3352-3356.

[15] 李崇坚.交流同步电机调速系统[M].北京： 北京科学出版社,2006.

[16] 王秀和.永磁电机[M].北京： 中国电力出版社,2007.

[17] 李言俊,张科.系统辨识理论及应用[M].北京： 国防工业出版社,2003.

[18] 李鹏波,胡德文.系统辨识基础[M].北京： 中国水利水电出版社,2006.

[19] 王春民,嵇艳鞠，栾卉等.Matlab/Simulink永磁同步电机矢量控制系统仿真[J].吉林大学学报： 信息科学版,2009,27(1)： 17-22.

[20] 王巍,侯利民,李洪珠.基于Simulink的PMSM矢量控制系统仿真研究[J].自动化技术与应用,2008,27(2)： 43- 45.