平面向量复习要强化“5种意识”的培养

●

(元济高级中学 浙江海盐 314300)

作者简介卢明，1999年至今任海盐元济高级中学校长，现任浙江省中学数学教育学会理事、浙江省中小学信息技术教育学会理事、嘉兴市数学学会副理事长、嘉兴市教育学会理事、嘉兴市中小学信息技术教育学会理事、海盐县教育学会副会长.浙江省特级教师，省首批中小学正高级教师、浙派教育家发展共同体成员、省“5522”中小学名校长培养人选、嘉兴市首批中小学名校长、省“第16届春蚕奖”获得者、省劳动模范、嘉兴市新世纪专业技术带头人，连续4届被评为海盐县有突出贡献的专业技术人才、海盐县首批功勋教师.

主要社会兼职有：教育部中小学教师“国培计划”专家库成员、华东师范大学教研员研修中心特聘讲座教授、浙江省基础教育研究中心特聘教授、湖州师范学院客座教授、浙江省普通高中新课程实验工作专业指导委员会专家组成员、山东和海南省中小学教师新课程远程研修项目团队特聘专家、中国西部地区教育顾问.

主要科研成果有：近10年中，主持过3项省级规划课题、2项省级专项课题、4项嘉兴市级规划课题的研究，成果分别获得省级一、二、三等奖和嘉兴市一、二等奖，公开发表论文40多篇，曾承担国家级、省级、市级学术报告(讲座)100多场.

平面向量是高中数学的重要内容，也是高考的热点之一．平面向量作为一块独立的内容，有其自身的知识体系和独特的思想方法．它有别于代数、几何和三角，但又与它们有着紧密的联系．鉴于平面向量内容的上述特点，许多学生到了高三对向量学习尚未入门，没有形成“向量思想”，遇到较灵活的题不知所措，思维没有方向，错误率较高．高三平面向量复习如何解决以上问题，是困扰教师的一大难题．

笔者连续带了6届高三毕业生，结合自己对向量题目的解题规律研究，摸索出了一套从培养学生的“5种意识”入手，帮助学生形成“向量思想”，突破向量问题的解题困境，收到了良好的效果．现撰文与大家分享，以求共同探讨．

1 “投影”意识

所谓“投影”意识，就是能自觉运用向量的“投影”来解决实际问题的一种思维方式．其实，它是对向量数量积本质的理解和把握．向量的数量积是向量知识中非常重要的核心知识，但许多学生对它的掌握往往只停留在肤浅运用的层面，只会机械地套用公式、计算2个向量的数量积和求2个向量的夹角(或夹角的三角函数值)，缺乏对公式中隐含的“本质信息”——向量“投影”的意义和价值的认识．要想让学生较深刻地理解和把握向量数量积的概念，必须强调对向量“投影”概念的理解与应用．如：(1)让学生结合数量积公式，说出b在a方向上的投影如何表示？(2)结合图形，正确作出b在a方向上的投影；(3)通过直观图形，理解b在a方向上的“投影”|b|cos是一个数值，且可以为正数、0或负数，“投影”的符号取决于a与b夹角的大小，然后通过典型例题，进一步强化“投影”思想在解决实际问题中的运用．

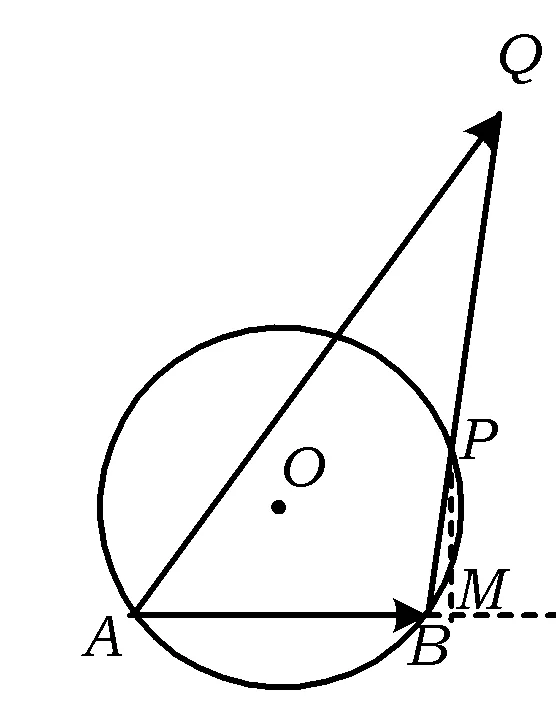
图1

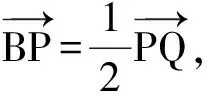
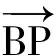
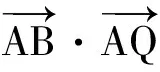
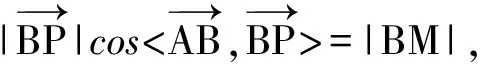
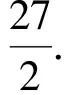
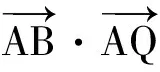
向量的“投影”思想在高考命题中也颇受关注．

( )

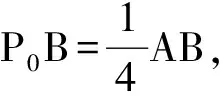
A．∠ABC=90° B．∠BAC=90°

C．AB=ACD．AC=BC

(2013年浙江省数学高考理科试题)

本题解法较多，然而运用“投影思想”和“排除法”，解题过程简洁且通俗易懂．

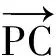
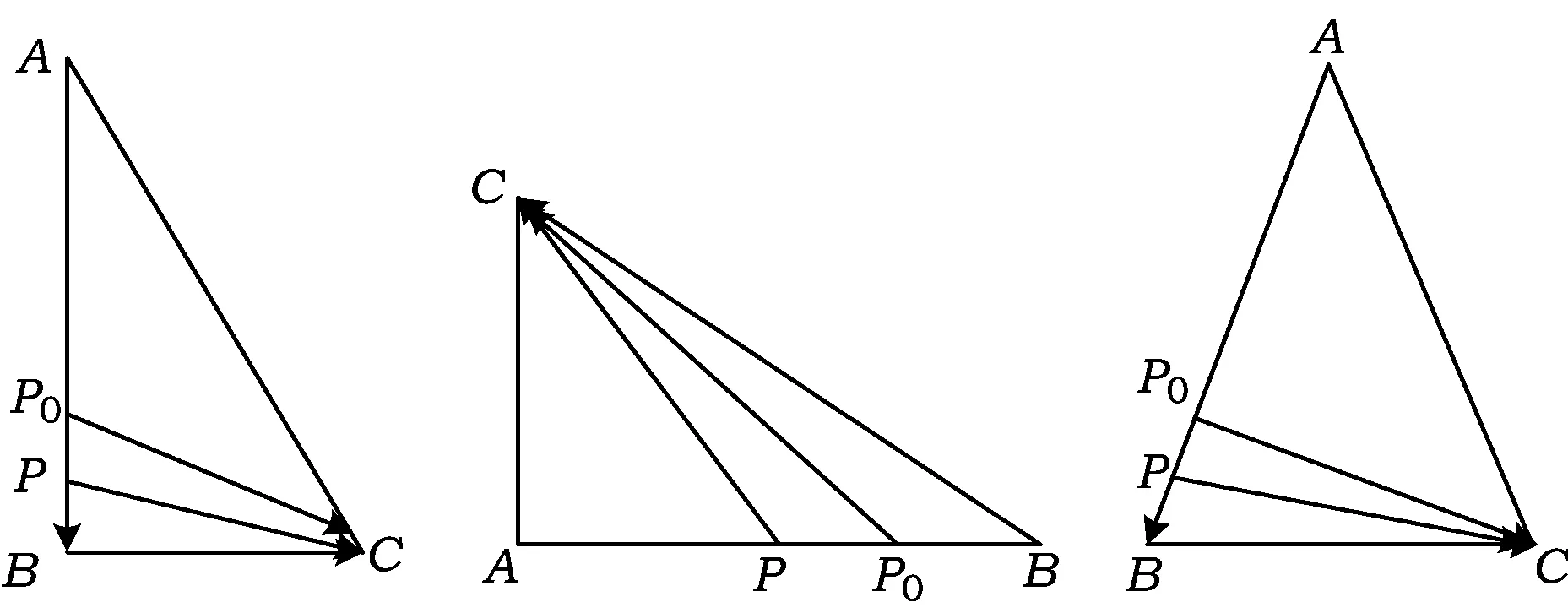
图2 图3 图4

若∠BAC=90°，设P为AB的中点，则P0是PB的中点(如图3)，于是

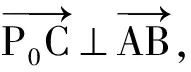
综上所述，选项D正确．

2 “几何”意识

所谓“几何”意识，是指能主动挖掘向量问题的几何背景用以解题的一种思维方式．这种解题方法称之为“几何法”．我们知道，向量不仅拥有数的特性，还有形的特性，如向量的加法、减法符合平行四边形法则和三角形法则；再如，若|a|=2，则向量a的几何背景可以与圆建立联系，等等．如果能将向量问题置于适当的几何背景之中，就能够使抽象问题直观化，实现快速解题之目的．纵观历年浙江省平面向量高考试题的命题风格，几乎每道题都有一定的几何背景，这种命题风格充分体现了对向量本质和数形结合思想的考查，突出了对考生思维灵活性和空间想象能力的检测．因此在复习时，一方面要启发学生主动挖掘向量的几何背景，另一方面要让学生注意总结向量问题中常用的一些几何图形和几何元素．笔者认为，向量问题中常用的几何图形主要有平行四边形、三角形和圆；常用的几何元素主要有平行四边形的对角线，三角形的边、中线、外心、重心、垂心，圆的半径、圆周角、圆心角等．

例3已知a,b是平面内2个互相垂直的单位向量，若向量c满足(a-c)·(b-c)=0,则c的最大值是

( )

(2008年浙江省数学高考理科试题)

解由(a-c)·(b-c)=0知向量(a-c)⊥(b-c)，故可联想到直径上的圆周角．构造圆O，使向量a-c和b-c的夹角恰为直径上的圆周角(如图5)．

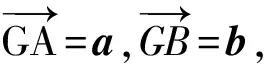
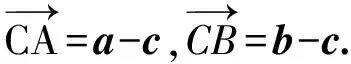
由a⊥b得AB为直径，故

(a-c)⊥(b-c)，

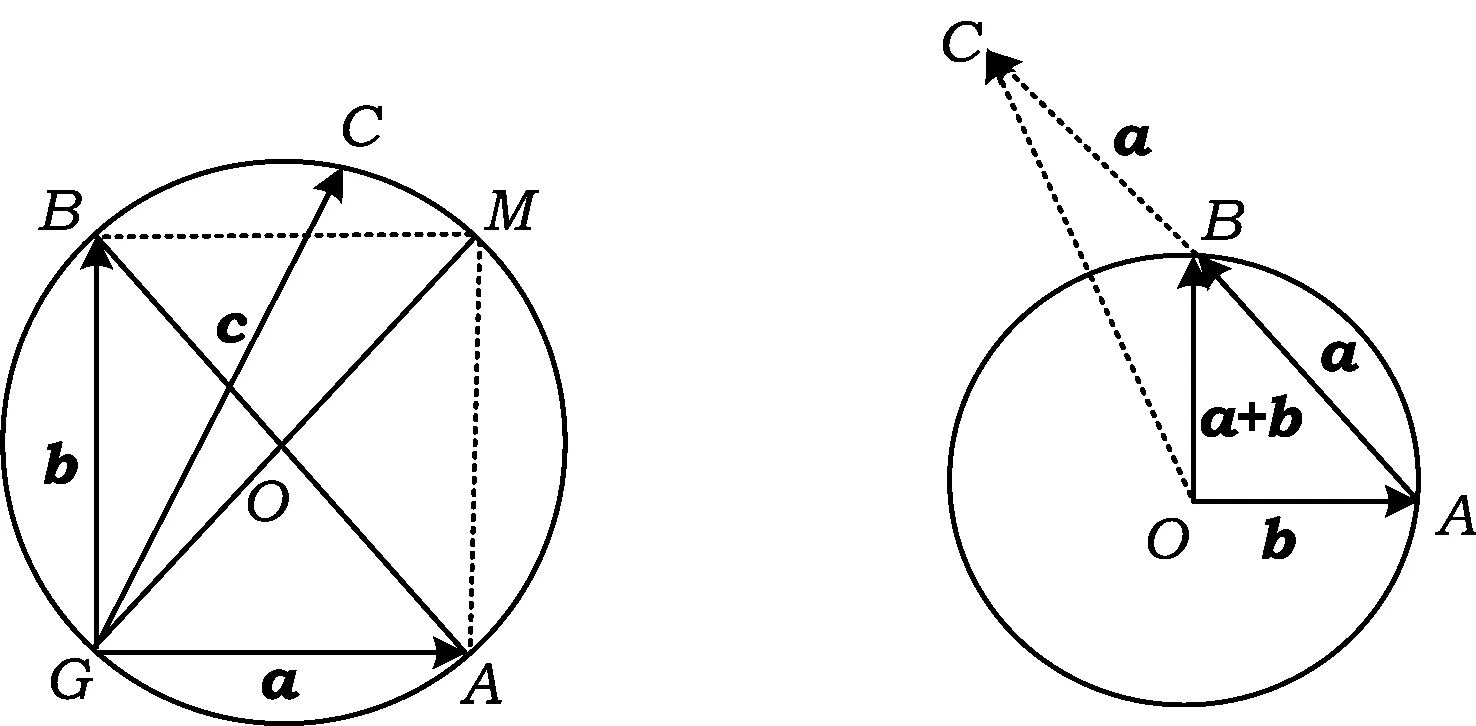
图5 图6

例4若非零向量a,b满足|a+b|=|b|，则

( )

A．|2a|>|2a+b| B．|2a|<|2a+b|

C．|2b|>|a+2b| D．|2b|<|a+2b|

(2007年浙江省数学高考理科试题)

分析注意挖掘|a+b|=|b|的“几何背景”，将它们看作是一个圆的2条半径．

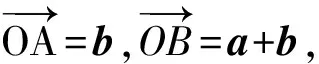
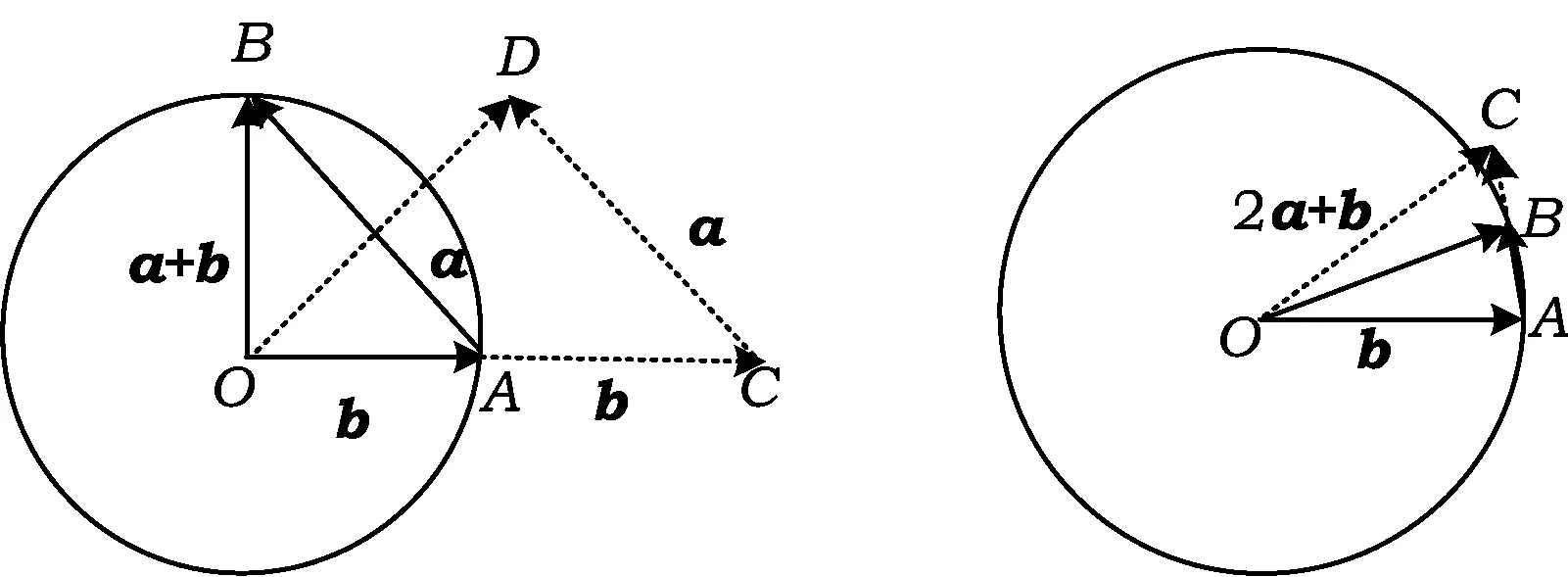
图7 图8

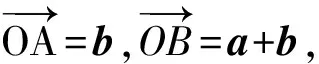
综上所述，选项C正确．

点评以上解法，通过挖掘向量的几何背景，利用数形结合的方法，对一些几何元素进行分析，避免了复杂的运算过程，既直观又形象，达到了事半功倍的效果．在构造几何图形的过程中，充分发挥了学生的空间想象力，促进了数学思想的形成．

3 “坐标”意识

所谓“坐标”意识，是指通过构建直角坐标系，将向量改用坐标来表示，使向量问题转化为代数问题来处理的一种思维方式．这种解题方法称之为“坐标法”．“坐标法”是解决向量问题的一条重要途径，其优点是思维方式比较“固定”，学生容易掌握，关键是合理建立直角坐标系，准确算出关键点的坐标．为强化学生的“坐标”意识，可以经常提醒学生，当用别的方法难以奏效时，不妨用“坐标法”来尝试一下．

例5已知向量a,b满足|a|=|b|=a·b=2，且(a-c)·(b-2c)=0，则|b-c|的最大值为______．

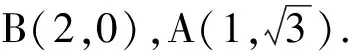
(a-c)· (b-2c)=

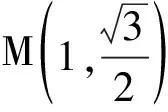
显然，当C运动到点B与点M之间，且点B,C,M共线时，

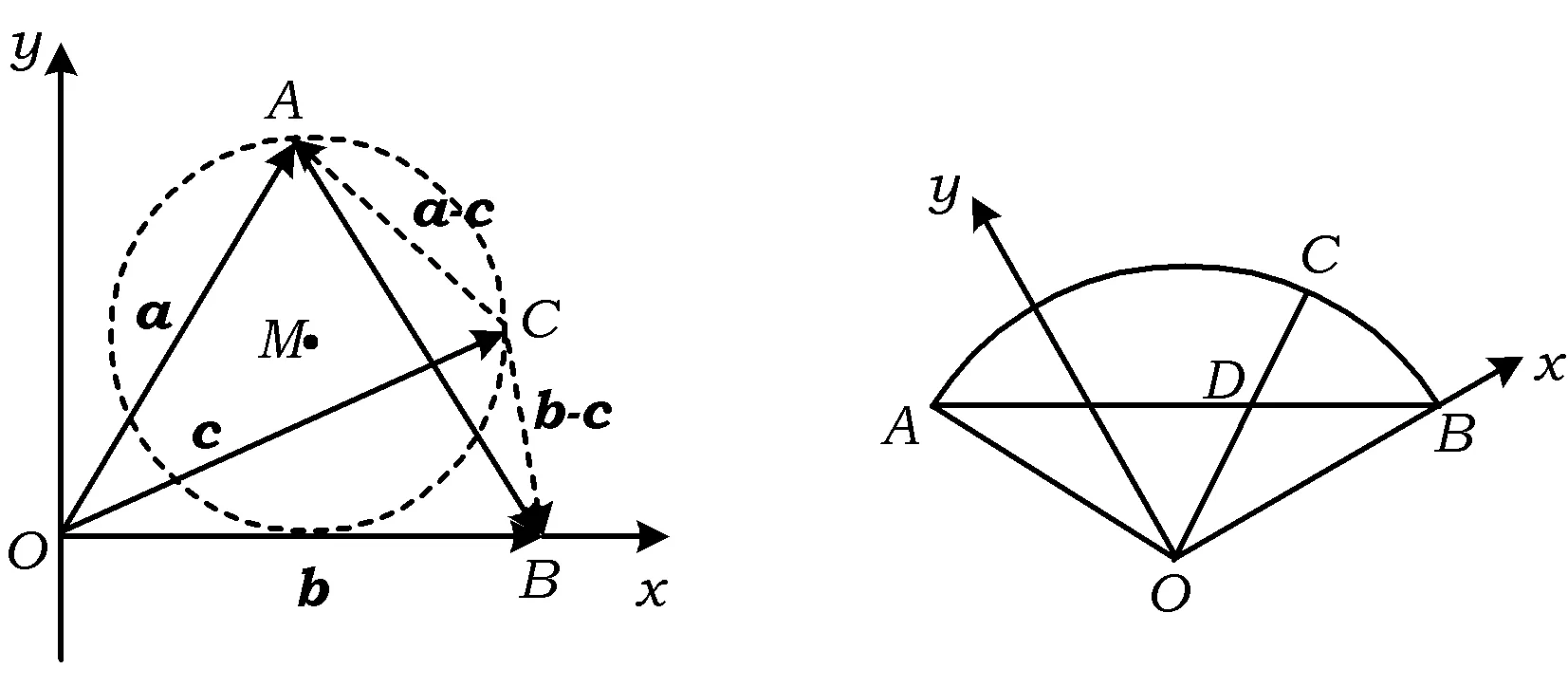
图9 图10

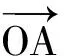
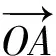
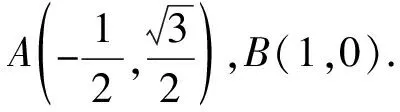
于是

从而

1≤x+y≤2．

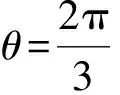
点评教师要提醒学生：在构建坐标系时，2个坐标轴不一定要处于“标准”位置．对于可变向量c的坐标的设法可以有不同的形式，如例5采用的是“实数式”，变式采用的是“参数”(θ为参数)，目标都是为了构造熟悉的问题情境，从而方便后面的计算，实现解题策略的优化．

如果将变式中的“求x+y的最值”改为“求x+3y的最值”，请读者尝试解答一下，进一步体会“坐标法”的优势．

4 “点积”意识

所谓“点积”意识，就是在一个含有向量关系的等式2边同时“点积”一个适当的非零向量，把向量关系的等式转化为代数方程，实现化简之目的的一种思维方式．用到的知识点还是向量的数量积，问题的关键是要斟酌“点积”一个什么向量容易达成化简目的．“点积”也包括对含有向量关系的等式2边同时进行平方，下面结合实例进行说明．

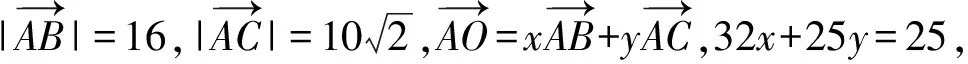
解三角形的外心是3条边中垂线的交点．设D,E分别为AB,AC的中点(如图11)，则

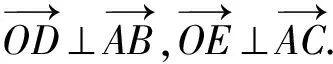
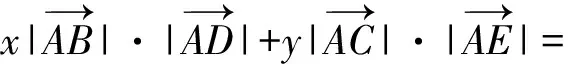
128x+100y=4(32x+25y)=100,

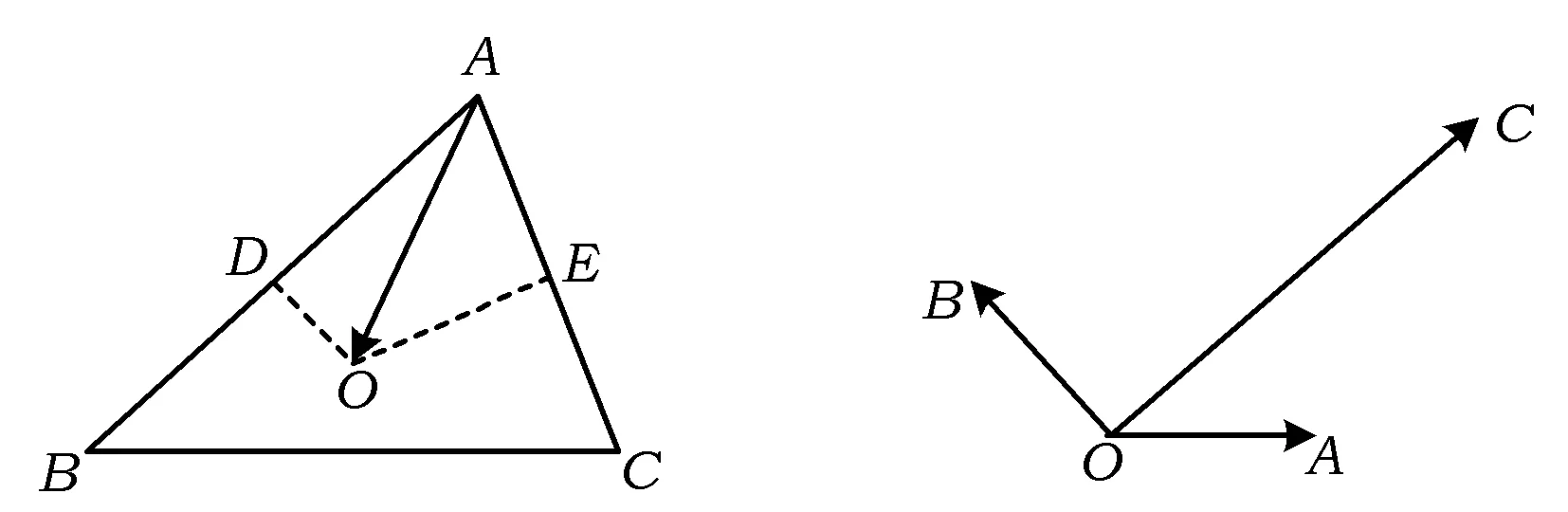
图11 图12

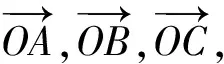
(2007年陕西省数学高考理科试题)

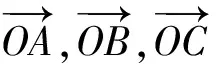
即

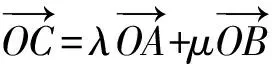
5 “基底”意识

所谓“基底”意识，是指有预见性地选择适当的“基底”，并用“基底”来表示有关向量，以实现化归的一种思维方式．“基底”意识的本质是平面向量基本定理的灵活运用，难点是如何选择“基底”有利于简化运算．下面结合实例加以说明．

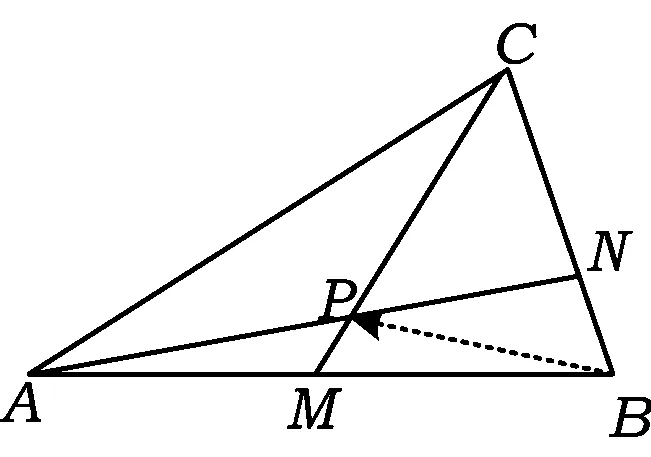
图13

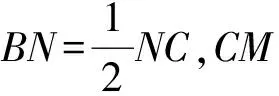
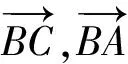
又点A,P,N共线，同理

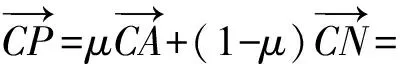
由式(1)，(2)得

故

CP∶PM=4∶1．

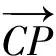
又点A,P,N共线，于是

由式(3)，(4)得

故

CP∶PM=4∶1．

点评由例8的2种解法不难发现，“基底”选的是否恰当直接影响解题过程的简洁性．2种解法中多处涉及到了3个点共线时如何选择“基底”．要使学生能够具备有预见性地选择“基底”的能力，需要平时有意识地加强培养，帮助学生积累经验．

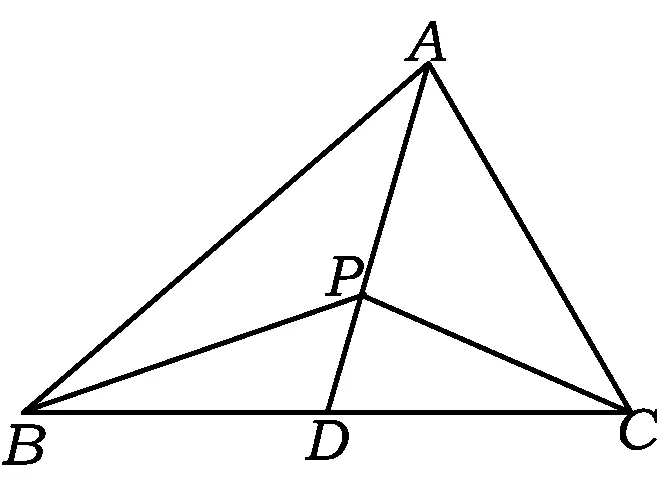
图14

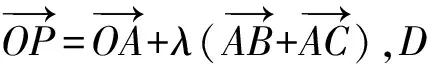
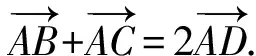
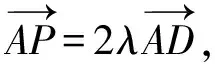
故点A，P，D共线．

再由“中线向量”模型得

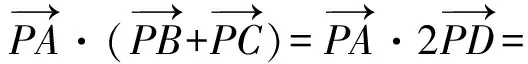
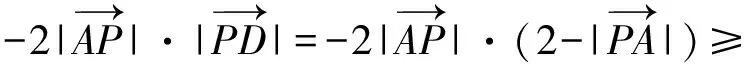
点评例9的解答2次用到了三角形“中线向量”模型．

总之，平面向量复习强调关注学生“5种意识”的培养，其目的就是帮助学生解决向量学习的入门问题，即“授之以渔”．有了这“5种意识”，学生就能形成“向量思想”，能够在解决实际问题时迅速找到思维的突破口，形成有效的思维成果．需要指出的是，这“5种意识”对应着5种不同的解题方法，每一种方法都有其优势和局限性．不同的问题需要用不同的方法，尽管有的问题可以用多种方法去解决，但是仔细考量后不难发现：不同的方法其解题过程的复杂程度差异较大．

数学学习追求的不仅仅是把题做“对”，更看重的是要把题做“好”，即追求解题策略的“最优化”．为此，只让学生拥有这“5种意识”还不够，还要在面对具体问题时能够迅速作出判断，选择“最优化”解题策略．这是一种学习境界，要达到这样的境界，需要伴随丰富的学习经历和经验的积累，而不是简单的模仿操练．以笔者之见，知识不是教师教会的，而是学生自己学会的，学习应该是学生亲力亲为的事，别人无法替代．基于这样的认识，笔者在向量复习时非常重视学生学习经历的设计，精心组织课程资源，积极创造条件让学生多尝试、多交流，鼓励学生一题多解，在各种不同的解法中让学生自己去比较、体会、发现规律，积累经验，从而提升能力．