基于层次分析法的运输提升限制因素权重分析

薛振林 吴爱祥 王贻明 黄明清 杨 鹏

(1.北京科技大学土木与环境工程学院，北京 100083;2.金属矿山高效开采与安全教育部重点实验室，北京 100083)

基于层次分析法的运输提升限制因素权重分析

薛振林1,2吴爱祥1,2王贻明1,2黄明清1,2杨 鹏1,2

(1.北京科技大学土木与环境工程学院，北京 100083;2.金属矿山高效开采与安全教育部重点实验室，北京 100083)

为更科学合理地优化矿山运输提升系统，在分析某矿山运输提升运行限制因素的基础上，运用层次分析法建立了这些限制因素的AHP层次结构模型。通过构造判断矩阵和AHP模型的求解，得到了限制因素的权重结果：其中多级提升效率低权重比例最大，达35.2%，斜井缺乏统一设计和中段运输效率低权重分别达到15.04%与14.55%，其余各因素均未达10%。单排序和总排序判断矩阵一致性检验均有，一致性良好。表明通过层次分析法确定矿山运输提升运输系统限制因素相对重要性是可行的。分析结果为运输提升系统的优化决策提供了依据，进而给出优化意见，重点从改善多级斜井串车提升方式、做好深部运输提升的统一设计和发挥大中段运输作用3方面进行。

运输与提升 层次分析法 权重分析 AHP

矿山运输提升系统是矿山生产作业的关键环节之一，其安全高效的运行是地下矿山正常生产的重要前提，其合理性与高效性直接影响着矿山生产能力和企业效益的提高。在矿山生产过程中，运输提升任务主要是运送和提升矿石、废石、材料、设备和人员等。国内很多矿山由于设计之初缺乏长远考虑，并未进行深部探矿工作，或者前期设计规模较小，后期需要进行扩产等，致使现有的运输提升系统制约着矿山产量的提高，成为企业发展的瓶颈问题。很多矿山亟需对现有运输系统进行优化设计，从而保证矿山提升运输工作长期高效的进行。然而在运输提升系统的优化工作中，由于限制因素较多，不同矿山限制因素也不尽相同，这就给优化的决策带来了一定的困难。如果不充分调查实际情况、不分重点地盲目优化，效果必定不够理想，也会带来不必要的经济损失。目前，针对此类具有不确定性多因素的决策问题，国内外学者研究出很多的优选方法，常用的主要有专家评价法、层次分析法、投影寻踪法，神经网络法等[1]。这些方法具有各自的特点和使用范围，且在某些方面各有优势。层次分析法具有可以利用少量的信息使决策的思维过程数学化的特点，从而为复杂的决策问题提供简便而实用的决策参考依据[2]。

1 某矿山运输提升系统概述

云南某矿为铅锌为主的多金属矿山，年产能力120万t/a，现有4个工区同时生产作业。但各工区的运输提升系统相对独立，未形成统一协同作业，运输提升系统复杂多变。各工区开拓方案主要为平硐+多级盲斜井联合开拓或单独的多级斜井开拓，提升系统主要采用斜井单钩串车提升，井下运输以人力推车方式为主，主要运输中段采用少量柴油机或电机车牵引串车。随着开拓深度的增加，提升已多达4～5级，既增加了提升的费用，又增加了安全风险。同时，设备老化和设备选型缺陷等问题也影响着效率的提高，矿山亟需对现有运输系统进行优化设计。经过现场调研可知，该矿山生产过程中暴露出运输提升限制因素较多，各因素相互作用且相互影响，形成了一个复杂系统，给系统优化工作带来了一定的困难。

AHP层次分析法在各种工程决策分析问题和复杂问题的多因素权重分析方面有其独到的优势，有着广泛的应用[3-6]。它可以在对运输提升系统优化问题的本质、效率提高的限制性因素及其内在关系等进行深入分析的基础上，用数量的形式条理化、科学化的表达人的主观想法。可避免由于主观原因导致的权重计算结果与实际情况相矛盾的现象产生[7-8]。所以，对于该矿山运输提升系统权重分析及其优化的问题，其决策结果难以直接准确计量，采用AHP层次分析法尤其适合。

2 运输提升限制因素权重分析

2.1 建立层次结构模型

为了能够更具有针对性的对现有问题进行优化和改善，在深入分析运输与提升系统制约因素的实际问题基础上，根据层次分析法的基本步骤，分析该体系所包含各因素及各因素之间的相互关系。将限制因素进行分类整理，按照不同从属类别将层次结构自上而下地分为3个层次。目标层为运输提升限制因素权重分析；准则层分为3个影响因素，分别为设计问题、设备和技术问题、人员操作问题；子准则层分为9个因素，分别为缺乏统一设计、提升能力不足、多级提升效率低、中段运输效率低、设备选型不合理、机械化程度低、钢丝绳寿命短、员工安全意识差、提升员工不足。从而建立了提升运输限制因素递阶层次结构模型，如图1。

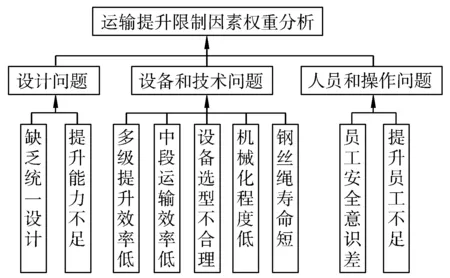
图1 运输提升系统限制因素权重分析层次结构模型Fig.1 Weighting analysis hierarchy model of transport hoisting system limiting factors

2.2 构造判断矩阵

在建立模型的层次结构后，对于从属于同一个因素的每个限制因素进行两两比较，按Satty等人提出的1～9级标度法比较其重要程度，从目标层至9个限制因素间依次构造成判断矩阵[9-10]。运输提升限制因素的判断矩阵中，1～9标度具体含义的确定，主要是在矿山现场调研基础上，根据矿山单位与采矿行业专家评估给出，或由之前类似矿山历史经验数据得出。1～9标度意义如表1。

表1 1～9标度的意义Table 1 The meaning of 1-9 scaling

针对本矿山的运输提升限制因素递阶层次结构模型，由顶层开始分别对各级进行编号：A；B1，B2，B3；C1，C2，…,C9。结合根据本矿山实际情况确定的标度级别意义，对模型第一层与第二层，第二层与第三层之间的各级相互影响因素构造判断矩阵如下。

目标层A与准则层B之间构造判断矩阵

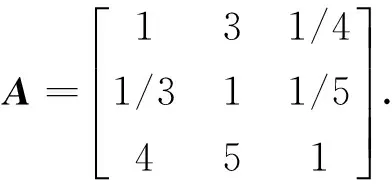
(1)

准则层B1与子准则层C1，C2之间构造判断矩阵

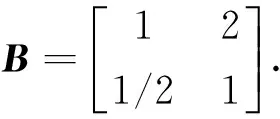
(2)

准则层B2与子准则层C3，C4，C5，C6，C7之间构造判断矩阵

(3)

准则层B3与子准则层C8，C9之间构造判断矩阵

(4)

2.3 计算权向量并做一致性检验

对于每一个判断矩阵，计算各因素针对其所属准则的权重。计算权向量，判断矩阵A对应于最大特征值λmax的特征向量W，经归一化后为相应因素对于上一层次因素相对重要性的排序权值。权重和权向量计算结束后，需对结果进行一致性检验。只有通过检验，才能表明判断矩阵在逻辑上是合理的，进而对结果进行后续分析。若不具有一致性，需重新构造成对比较阵。

对判断矩阵进行一致性检验，需计算

CI=CI/RI，

(5)

式中，CR为一致性比例，当CR=0时，判断矩阵具有完全的一致性；当CR<0.10时，判断矩阵的一致性认为是可以接受的，CR越大，一致性越差。CI为一致性指标，按下式计算：

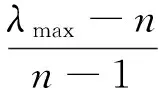
(6)

式中，λmax为判断矩阵的最大特征根；n为成对比较因子个数；RI为随机一致性指标，如表2。

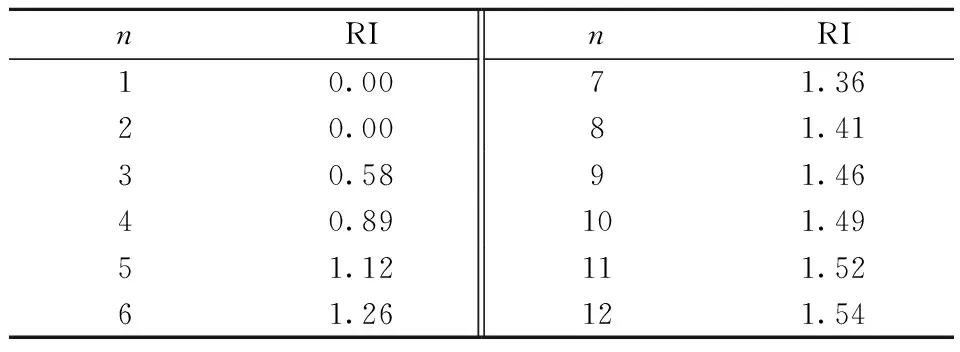
表2 随机一致性指标RI值Table 2 Random consistency index RI values

分别计算矩阵A、B1、B2、B3最大特征根及对应特征向量，并利用随机一致性指标和一致性比率做一致性检验，结果如下。

A矩阵：运输提升限制因素权重分析，矩阵最大特征值λmax=3.085 8，矩阵特征向量W=(w1,w2,w3)=(0.025 5,0.100 7,0.673 8)，一致性比例CR=0.082 5<0.1，一致性是可以接受的。对运输提升制约因素的权重1.000 0。

B1矩阵：设计问题，矩阵最大特征值λmax=2.000 0，矩阵特征向量W=(w1,w2)=(0.666 7，0.333 3)。一致性比例CR=0.000 0<0.1，一致性是可以接受的。对运输提升制约因素的权重0.225 5。

B2矩阵：人员和操作问题，矩阵最大特征值λmax=2.000 0，矩阵特征向量W=(w1,w2)=(0.250 0,0.750 0)。一致性比例CR=0.000 0<0.1，一致性是可以接受的。对运输提升制约因素的权重0.100 7。

B3矩阵：设备和技术问题，矩阵最大特征值λmax=5.389 1，矩阵特征向量W=(w1,w2,w3,w4,w5)=(0.426 5,0.245 0,0.134 2,0.107 8,0.086 5)。一致性比例CR=0.086 9<0.1，一致性是可以接受的。对运输提升制约因素的权重0.100 7。

各矩阵权向量与一致性计算结果表明，所有单排序的矩阵一致性比例CR<0.1，所以每个判断矩阵的一致性均是可以接受的。

2.4 总排序及一致性检验

要最终得到各元素特别是子准则层各影响因素对于目标的权重，需要进行权重的总排序。总排序是所有因素对于目标层的重要性的排序权重。利用同一层次所有的单排序的结果，通过逐层计算相对权重，即可得到最底层各限制因素对目标层的总权重。计算运输提升系统中各限制因素对目标层的总权重并进行排序，如表3。

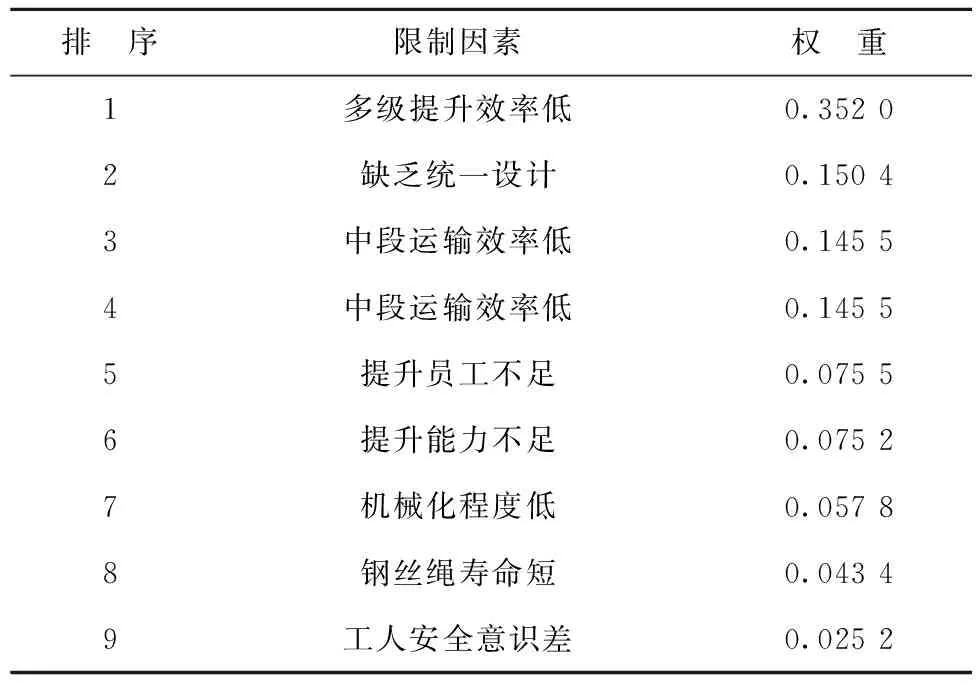
表3 运输提升系统限制因素权重排序Table 3 Transport hoisting system limiting factors weighting results

对总排序进行一致性检验，计算总权重一致性：

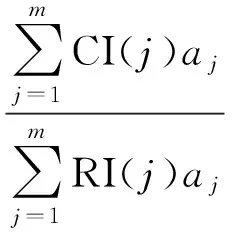
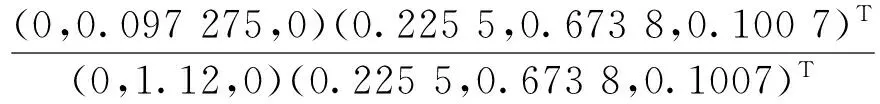
0.086 852 68<0.1.

可以认为，总排序的一致性是可以接受的。因此，用层次分析法对矿山运输提升运输系统限制因素进行权重分析，确定各限制因素之间的相对重要性程度是可行的。

2.5 结果与建议

权重分析结果表明，在诸多限制因素中多级提升系统效率低占据了最大的权重，达到35.2%，这说明多级斜井串车提升方式是制约该矿山运输提升系统的最主要因素。斜井缺乏统一设计和中段运输效率也占据了较大比重，这2个限制因素权重分别达到了15.04%与14.55%，而其余各因素均为超过10%。

各限制因素权重分析结果为优化运输提升系统的开展提供了依据。下一步优化工作应以此权重分析结果为依据进行，重点完成高权重限制因素优化。首先，针对多级斜井串车的提升方式进行优化，结合矿山实际提出3种备选优化方案：单一竖井提升、平硐加盲竖井、平硐加盲斜井提升，然后进行后续的方案设计和优选工作。其次，做好深部运输提升的统一设计工作，由矿山技术科人员联合科研单位共同完成4个工区整体设计，改变以往各工区自行组织的格局，减少重复工作。最后，要重视发挥大运输中段的作用，合理设计级数、位置、数量和连接中段，以大运输中段间定期稳定提升作业形式代替多斜井、多中段、分散作业的形式。增强机械化作业方式，通过电机车集中运输，增强提升工作能力，全面改善矿山运输提升系统面貌。重点优化工作完成后可根据权重分析结果进行针对后续限制因素的优化工作。

3 结 论

(1)针对矿山运输系统亟需优化的实际情况，在分析运输提升系统实际运行限制因素的基础上，运用层次分析法建立了矿山运输提升系统限制因素的3层递阶层次结构模型。

(2)通过构造判断矩阵和求解AHP模型得到一致性检验均有CR<0.1，表明单排序和总排序判断矩阵均具有良好的一直性。说明通过层次分析法对矿山运输提升运输系统限制因素进行权重分析，确定各限制因素相对重要性是可行的。

(3)多级提升系统效率低占据了最大权重，达到35.2%，斜井缺乏统一设计和中段运输效率权重分别达到了15.04%与14.55%，而其余各因素均为超过10%。权重分析结果为提升运输系统评价及优化决策提供了依据，优化工作重点从多级斜井串车提升方式、做好深部运输提升的统一设计工作、重视发挥大运输中段的作用3方面进行。

[1] 荆全忠，姜秀慧，杨鉴淞,等.基于层次分析法(AHP)的煤矿安全生产能力指标体系研究[J].中国安全科学学报，2007，9(16)：74-79. Jing Quanzhong，Jiang Xiuhui，Yang Jiansong，et al.Study on index system of capability of production safety in coal mine based on AHP[J].China Safety Science Journal,2007，9(16)：74-79.

[2] Saaty T.The Analytic Hierarchy Process[M].New York：McGraw-Hill Inc，1980.

[3] 郭金玉，张忠彬，孙庆云.层次分析法的研究与应用[J].中国安全科学学报，2008，18(5)：148-153. Guo Jinyu，Zhang Zhongbin，Sun Qingyun.Study and applications of analytic hierarchy process[J].China Safety Science Journal，2008，18(5)：148-153.

[4] 白怀良，钟 铁，常前发.用模糊层次分析法优选矿山废水治理方案[J].金属矿山，2007(4)：71-73. Bai Huailiang，Zhong Tie，Chang Qianfa.Application of fuzzy analytic hierarchy process in optimization of scheme for acid mine drainage treatment[J].Metal Mine，2007(4)：71-73.

[5] 龚 剑,胡乃联,张延凯,等.基于AHP-FCE法的高海拔地区采矿方法优选[J].金属矿山,2013(9):1-5. Gong Jian，Hu Nailian，Zhang Yankai，et al.Optimization of mining methods in high-altitude areas based on AHP-FCE[J].金属矿山,2013(9):1-5.

[6] 王新民，赵 彬，张钦礼.基于层次分析和模糊数学的采矿方法选择[J].中南大学学报:自然科学版，2008，39(5)： 875-880. Wang Xinmin，Zhao Bin，Zhang Qinli.Mining method choice based on AHP and fuzzy mathmetics[J].Journal of Central South Uinversity:Science and Techologyedition Edition,2008，39(5):875-880.

[7] 刘亚静，毛善君，姚纪明,等.基于层次分析法的煤矿安全综合评价[J].矿业研究与开发，2007，27(2)：82-84. Liu Yajing，Mao Shanjun，Yao Jiming，et al.Comprehensive safety evaluation of coal mine based on analytic hierarchy proces.

[8] 陈 桥，胡 克，雒昆利，等.基于AHP法的矿山生态环境综合评价模式研究[J].中国矿业大学学报，2006,3(25):377-383. Chen Qiao，Hu Ke，Luo Kunli，et al.Study on synthetical assessment model of mine eco-environments based on AHP[J].Journal of China University of Mining & Technology,2006，3(25):377-383.

[9] 朱 茵,孟志勇,阚叔愚.用层次分析法计算权重[J].北方交通大学学报，1999,5(23)：119-122. Zhu Yin，Meng Zhiyong，Kan Shuyu.Determination of weight value by AHP[J].Journal of Northern Jiaotong University，1999,5(23)：119-122.

[10] 常建娥，蒋太立.层次分析法确定权重的研究[J].武汉理工大学学报：信息与管理工程版，2007，29(1)：153-156. Chang Jian′e，Jiang Taili.Research on the weight of coefficient through analytic hierarchy process[J].Journal of Wuhan University of Technology:Information & Management Engineering Edition，2007，29(1)：153-156.

(责任编辑 徐志宏)

Weighting Analysis of Transportation and Lift Limiting Factors Based on AHP

Xue Zhenlin1,2Wu Aixiang1,2Wang Yiming1,2Huang Mingqing1,2Yang Peng1,2

(1.CivilandEnvironmentalEngineeringSchool，UniversityofScienceandTechnologyBeijing，Beijing100083，China；2.StateKeyLaboratoryofHigh-EfficientMiningandSafetyofMetalMinesMinistryofEducation，Beijing100083，China)

In order to reasonably optimize the mine transportation and hoisting system，an AHP(Analytic Hierarchy Process)model of haulage and hoisting limiting factors was established based on the analysis of the factor limiting the transportation and hoisting operation in a certain mine by using the AHP.The weights of the limiting factors were obtained by constructing judgment matrix and solving the AHP model.The multistage lift was low efficient and had the largest weight of 35.2%.The shaft lacks of unified design and the transport efficiency at middle is lower.These two factors' weight occupied 15.04% and 14.55%，respectively.The rest of the factors were not up to 10%.The judgment matrix consistency of single order and the total order are checked as with good consistency.The results showed that it was feasible to obtain the relative importance of limiting factors in mine transport and hoisting transport system by AHP.The analysis results provided the basis for optimizing decision and some recommendations were given.The work should focus on improving the multistage slope lift way，accomplishing the uniform design in deep transportation promotion and paying attention to sublevel haulage.

Transportation and lift，Analytic hierarchy process，Weight analysis，AHP

2013-11-09

国家“十二五”科技支撑计划项目(编号：2012BAB08B02)，国家自然科学基金重点项目(编号：50934002)，国家自然科学基金项目(编号：51104011)。

薛振林(1988—)，男，硕士研究生。

TD52

A

1001-1250(2014)-03-124-04