淮河蚌埠以下河道治理前后糙率变化

王守勤,胡 星,储德义

(1.中水淮河规划设计研究有限公司,安徽蚌埠 233001;2.水利部淮河水利委员会,安徽蚌埠 233001)

淮河蚌埠以下河道治理前后糙率变化

王守勤1,胡 星1,储德义2

(1.中水淮河规划设计研究有限公司,安徽蚌埠 233001;2.水利部淮河水利委员会,安徽蚌埠 233001)

为了给平原河道治理工程提供参考和借鉴,针对淮河蚌埠以下河道建立一维水动力模型,采用1991年及2008年测量的河道断面资料及相应的实测洪水资料率定模型,就河道治理前后的糙率参数变化进行分析评价。结果表明:对于无水生植物生长的平原河道,经过挖泥船水下作业、局部堤防退建、抛石护岸等治理后,主槽和滩地的糙率均有不同程度的增加。

河道糙率;平原河流;水下挖疏;堤防退建;抛石护岸;淮河

河道糙率作为表征水流能量沿程损失的重要参数,不仅是河流水沙输移模拟中必须考虑的问题,而且该参数的取值对河道治理规划设计也起到至关重要的作用。河道糙率选择正确与否,直接影响河道的防洪安全和防洪措施安排。曼宁糙率系数表问世以后,人们采用查表法选用糙率,虽然简便,但表中只有影响因素的定性描述,缺乏定量指标,加之制表时对影响因素归纳不全,选用糙率时带有很大的主观任意性和经验性,难以获得满意的成果[1]。因此,探求糙率的变化规律一直是水力学中重要研究课题之一。

随着计算机和数值计算技术的提高,糙率自动反演成为水力学计算中备受关注的课题,国内外学者对此做了诸多研究。Becker等[2]构建了一个关于明渠非恒定流参数辨识的影响系数算法来对糙率进行反演计算。Fread等[3]将河网分解成单个河道分别进行校正,采用最小化误差进行参数优化反演,取得了一定成果,只是在实际工程中河网是个复杂的系统,如果将河网分成单个河道进行反演工作量非常大,而且很多人工处理难免出现很大误差。金忠青等[4]从糙率的物理意义出发,根据河道规模及水力特性,将河道分成若干等级,将同一级河道看成相同的糙率,并将各级糙率的率定问题,提为反问题中的参数,首先根据实测资料,选择水位过程或流量过程作为目标函数的变量,构建各河段误差平方和目标函数。董文军等[5]对一维圣维南方程中曼宁糙率的参数辨识问题进行了研究与计算。李光炽等[6-7]提出了利用卡尔曼滤波来求解河道糙率,应用离散优化方法求解一维河道糙率的分布。

本文选取一段平原河道,建立一维水动力模型,采用1991年、2008年的实测河道断面资料及相应的洪水资料率定模型,就河道治理前后的糙率参数变化进行分析评价,以期为今后更加科学地进行工程规划设计和平原河道治理提供参考和借鉴。

1 河道概况

选取的河段为淮河中游蚌埠闸至洪泽湖入口河段,长约110km。从上游至下游,依次分布有蚌埠闸水文站(A)、吴家渡水文站(B)、临淮关水位站(C)、浮山水位站(D)和小枊巷水文站(E),该河段属平原河道,河道主槽为三级航道,河槽内无水生植物生长。

河道深泓高程一般为-7～7m(1985国家高程基准,下同),河道最低处深泓高程为-11.9m,最浅处深泓高程为7.77m,二者相差较大。总体而言,河段纵剖面为下凹型,总的趋势是以D为转折点,AD段平均深泓高程沿程降低,深泓高程为-10.78～7.77m,呈正比降,河底比降约为1/40000;而DE段河道平均深泓高程沿程增大,河床呈倒比降,河道纵剖面形态见图1。

图1 河道纵剖面形态

2 基础资料

水文资料主要是河道AE控制站1991年、2007年的汛期水位、流量资料,包括A、C、D站的水位过程与B、E站的水位及流量过程。地形资料主要是1991年及2008年测量的河道断面资料。

所选河道在1991年前的20多年间基本未进行疏浚治理,在1991—2005年,先后在AC段全面进行疏浚和堤防退建;CD段部分险工段进行护岸、切滩、退堤;DE段基本没有治理。在2005—2008年研究河道基本没有治理工程实施。因此选择1991年为治理前的典型年,2007年为治理后的典型年,分别以1991年、2007年的汛期实测资料对此河道的糙率进行率定。

3 计算模型

采用Preissmann四点隐式格式离散圣维南方程组,再利用三系数追赶法消元,得到河道首、末断面的水位、流量表示的方程,结合边界条件,解出节点水位后代回到各河段差分方程,求出各河段的流量和水位。描述河道水流运动的圣维南方程组[8-9]为

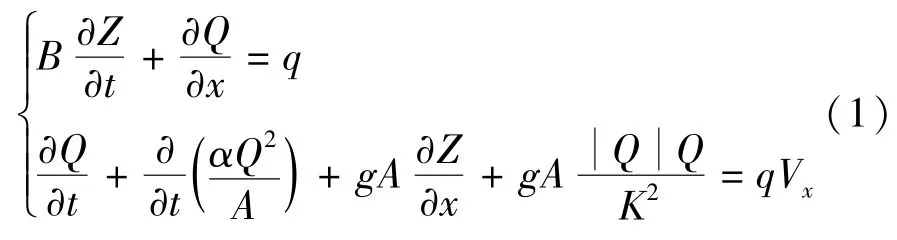
式中:q为旁侧入流流量;Q、A、B、Z分别为河道断面流量、过水面积、河宽和水位;Vx为旁侧入流流速在水流方向上的分量,一般可以近似为零;K为流量模数;α为动量校正系数;u为主流断面平均流速;g为重力加速度。

对断面i与断面i+1组成的河段Δxi,式(1)采用四点线性隐式差分格式进行数值离散,得任一河段的差分方程:

图2为计算河段示意图,节点I、J分别为河道的首节点、末节点。

图2 计算河段示意图

该河道共有L2-L1个河段,共有2(L2-L1)个差分方程,包含2(L2-L1)+2个未知量,以首节点和末节点的水位为自由变量,采用三系数追赶法消去中间断面的水位和流量,最后得到首、末断面的流量与首、末节点水位关系的方程:

采用分段率定的方法率定糙率,即将该河道分成AB、BC、CE这3段来分别率定各段的糙率。AB河段率定时上、下边界均采用水位边界,率定B站流量过程;BC河段率定时上边界采用B站流量过程,下边界采用C站水位过程,率定B站水位过程;CE河段率定时上边界采用C站水位过程,下边界采用E站水位过程,率定E站流量过程;AE整体演算时,上边界采用A站水位过程,下边界采用E站水位过程,分段率定糙率。

4 整治前后糙率分析

4.1 模拟结果

河道整治前后的糙率计算结果见表1,1991年及2007年河道沿程各站的水位峰值计算值与实测值对比见表2、表3,河道沿程各站的水位及流量过程计算值与实测值对比见图3～5。

表1 河道整治前后糙率计算结果

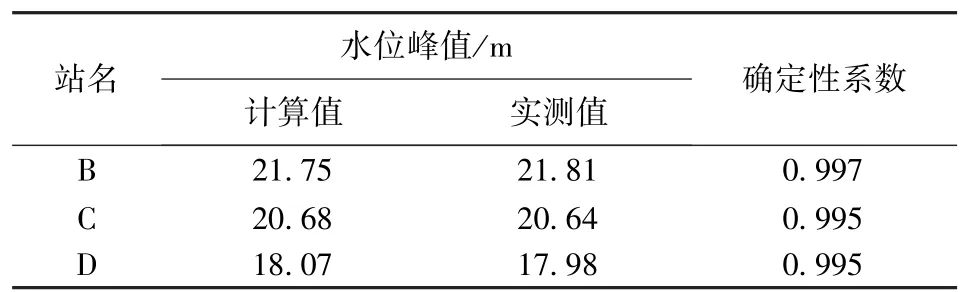
表2 1991年河道沿程各站的水位峰值计算值与实测值对比

表3 2007年河道沿程各站的水位峰值计算值与实测值对比

由表2、表3及图3～5可知,河道沿程各站的水位峰值计算值与实测值误差在10cm以内,水位及流量过程的计算值与实测值吻合较好,确定性系数均在0.99以上,据此分析计算结果满足精度要求。

4.2 结果分析

AE河段治理前后主槽和滩地糙率率定结果对比见表4、表5。由表4可知,AB河段主槽糙率治理后比治理前增加了13.51％;BC河段主槽糙率治理后比治理前增加了19.04％～6.38％;CD河段主槽糙率治理后比治理前增加了4.55％～8.70％;DE河段主槽糙率没有变化。治理后河段的主槽糙率均有不同程度的增加,其中BC河段主槽糙率治理前后变化最大,最大增加19.04％;AB河段主槽糙率治理前后变化也比较大,增加13.51％。

图3 1991年河道沿程各站的水位过程

图4 2007年河道沿程各站的水位过程

由表5可知,AB河段滩地糙率治理后比治理前增加了5.13％;BC河段主槽糙率治理后比治理前增加了1.29％～7.69％;CD河段主槽糙率治理后比治理前增加了3.90％～7.95％;DE河段滩地糙率没有变化。治理后河段的滩地糙率均有不同程度的增加,其中BC、CD河段滩地糙率治理前后变化最大,最大增加7.95％;AB河段滩地糙率治理前后变化也比较大,增加5.13％。

对于原来无水生植物生长的河槽,由于主槽经过水下挖泥船扩挖疏浚治理,使得原来平滑的河槽表面糙度加大,故而主槽糙率有所增加,如上述河段分析中的AB、BC两段;而CD河段河槽主要是对局部险工段采取抛石护岸,局部河槽的糙度有所增加,河段糙率略有增加;而DE河段没有经过任何治理,主槽糙率没有变化。

AB、BC、CD这3河段滩地的糙率由于受到局部退堤影响,滩地变宽,退出的滩区原来土地肥沃,植物生长较茂盛,加上退堤段防浪林的种植,使得滩区糙度增加,致使滩区糙率略有增加;DE河段没有经过任何治理,滩地糙率也基本没有变化。

图5 2007年河道沿程各站的流量过程

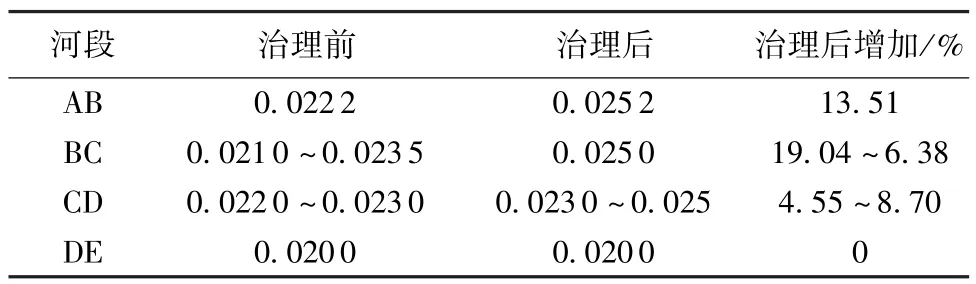
表4 AE河段治理前后主槽糙率率定结果对比

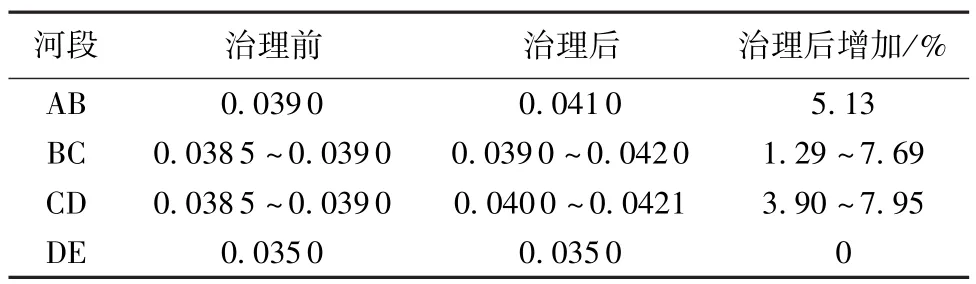
表5 AE河段治理前后滩地糙率率定结果对比

5 结语

a.对于宽浅自然河道而言,治理后河道糙率一般会有所减小,但由于影响河道糙率的因素错综复杂,对于本文研究的淮河中游蚌埠闸至洪泽湖入口河段,受工程措施实施导致的河槽粗糙、纵横断面等变化影响,河道治理后的糙率较治理前反而增加。因此,河道治理前后糙率变化应视具体情况研究确定。虽然研究河段河道治理后的糙率较治理前有所增加,由于治理后河道行洪断面面积增加,河道治理后的行洪流量较治理前还是增加的。

b.对于水生植物生长较少的平原河道,挖泥船水下作业而非水上明挖疏浚,局部堤防退建、抛石护岸等治理措施,可能导致原河道近期内主槽和滩地的糙率有不同程度的增加。但随着时间的推移,河床在水流的作用下也有可能趋于平滑稳定,河道主槽和滩地的糙率也可能会随之变化,这将有待今后对此进行跟踪研究。

c.河道糙率与河床组成、床面特征、平面形态、水流特征、岸壁特征等有关,它是反映河道阻力的综合系数。在制定河道治理规划目标时,可以对治理前后影响河道糙率的各种因素进行综合分析论证,合理确定规划参数和治理方案。

[1]袁世琼.天然河道的糙率计算[J].水电站设计,1997,13(1):82-85.(YUAN Shiqiong.Calculation of the roughness ofnaturalriverchannel[J].Designof Hydroelectric Power Station,1997,13(1):82-85.(in Chinese))

[2]BECKER L,YEH W W G.Identification of parameters in unsteady open channelflows[J].WaterResources Research,1972,8(4):956-965.

[3]FREAD D L,SMITH G F.Calibration techniques for 1-D unsteady flow models[J].Journal of Hydraulic Division,ASCE,1977,104(7):1027-1043.

[4]金忠青,韩龙喜.复杂河网的水力计算及参数反问题[J].水动力学研究与进展,1998,13(3):280-285.(JIN Zhongqing,HAN Longxi.Hydrodynamic calculation and parameter inverse problem for complex flow in open-channel networks[J].Journal of Hydrodynamics,1998,13(3):280-285.(in Chinese))

[5]董文军,杨则燊.一维圣维南方程的反问题研究与计算方法[J].水利学报,2002,9:61-65.(DONG Wenjun,YANG Zeshen.Calculation method for inverse problem of 1-D St.Venant equations[J].Journal of Hydraulic Engineering,2002,9:61-65.(in Chinese))

[6]李光炽,周晶晏,张贵寿.用卡尔曼滤波求解河道糙率参数反问题[J].河海大学学报:自然科学版,2003,31(5):490-493.(LI GuangZhi,ZHOU Jingyan,ZHANG Guishou.The Application of Kalman filter technique in inverse analysis of river channel roughness parameter[J].Journal of Hohai University:Natural Sciences,2003,31(5):490-493.(in Chinese))

[7]李光炽.流域洪水演进模型及其参数反问题研究[D].南京:河海大学,2001.

[8]李家星,赵振兴.水力学[M].南京:河海大学出版社,2001.

[9]芮孝芳.水文学原理[M].北京:中国水利水电出版社,2005.

Analysis of the river roughness of Huaihe River channels in lower reaches of Bengbu before and after its regulation

//WANG Shouqin1,HU Xing1,CHU Deyi2(1.China Water Huaihe Planning,Design and Research Co.,Ltd.,Bengbu 233001,China;2.The Huaihe River Commission of the Ministry of Water Resources,Bengbu 233001,China)

In order to provide reference for plain river regulation project,this study established a one-dimensional hydrodynamic mathematical model of Huaihe River channels in lower reaches of Bengbu,and then analyzed the roughness from beginning to the end of the river regulation based on the bathymetry from 1991 and the re-surveyed data in 2008.Overall,the results showed:in plain river channels without hydrophyte,the river roughness increased in varying degrees after river regulation including dredge of underwater operation,retreat built embankments and riprap bank.

river channel roughness;plain river;dredge of underwater operation;retreat built embankments;riprap bank;Huaihe River

TV133.2

:A

:1006-7647(2014)06-0062-04

10.3880/j.issn.1006-7647.2014.06.013

2013-09-24 编辑:周红梅)

王守勤(1963—),女,安徽亳州人,高级工程师,主要从事水利规划研究。E-mail:wangshouqin1@126.com