谈裂隙岩质边坡稳定性

杨 志 强

(北京华宇工程有限公司平顶山分公司，河南 平顶山 467002)

谈裂隙岩质边坡稳定性

杨 志 强

(北京华宇工程有限公司平顶山分公司，河南 平顶山 467002)

通过建立岩质边坡裂隙场网络模型，讨论了大孤山岩质边坡在裂隙场中的稳定性，结果表明连通度越大，风化越严重，坡体越容易沿连通度高的区域的潜在滑动弱面失稳破坏。

裂隙岩质边坡，稳定性，连通度

0 引言

岩质边坡稳定性的评价与预测是边坡工程研究的根本问题，也是边坡工程研究中最难和最迫切的课题之一[1]。随着国民经济的快速发展，矿山开采，交通运输，水利水电，国防工程等建设工程越来越多，工程开发就会对原有边坡进行人为改造，从而扰动或破坏了本来稳定的边坡，形成了新的人工边坡。大孤山露天矿高边坡就是在人类无序开采矿石下形成的，由于边坡在漫长的地质作用过程中，就一直存在潜在的变化，构造作用下边坡裂隙扩展发育，风化作用下边坡岩体物理化学性质渐变，如今在人类活动作用下边坡地貌特征改变。这些因素使得大孤山高边坡变得越来越复杂多变。其复杂多变性使得人们的认识受到限制，存在很多随机性、不确定性和模糊性[2]。但对其风化稳定性评价是非常必要的。

1 岩体裂隙网络模型

通常发育于岩石中的裂隙是有一定的展布规律的[3]，根据裂隙发育的宏观分布规律，可建立相应的裂隙场网络模型，通过裂隙场网络模型分析，可确定岩体裂隙场强度，即裂隙发育的连通程度。在岩体裂隙场中，裂隙发育的迹长总是有限长的，且由多组裂隙组成，通常按裂隙发育的空间方位特征来划分裂隙组[4，5]，可知同组的各个裂隙单体是互不相交，互不连续的。但只要不同方位的多组裂隙组彼此交切，就会构成在不同程度上相互连通的裂隙场网络系统。裂隙场连通度指用以说明裂隙场网络系统中裂隙连通程度的一种定量指标，其大小可反映出裂隙场网络系统的连通程度[6]。故根据其特性我们可作这样的规定：当连续裂隙场网络系统中每一条裂隙都无限延伸或与选取面域边界相交时，且每一条裂隙都相交，不是独立的单体，这样就可构成一相互连通的通路，其连通度量化为1，为极大值；相反，若裂隙场网络系统中各组裂隙互不相交，没有联系，不能形成一定的通路时，则其连通度量化为0，为极小值。因此在一般情况下，连通度的上下值是一个介于0与l之间的无量纲数。然而，我们所指的连通度不能代表裂隙的发育程度，它只是一个相对的概念。裂隙场网络系统中连通度的大小主要受裂隙发育的方向、组数、各组裂隙的迹长、密度、裂隙排列方式及裂隙连续系数等因素控制，其中大部分是属常规性的裂隙特征，不同之点在于后面两项，通常这些因素都可通过野外现场实测及现场研究确定，连续系数用以表示某一条或某一组裂隙的连续性，一般裂隙组是不连续的，所以连续系数也是一个介于0与l之间的无量纲数，用δ表示。若裂隙在切面上与外界是连通的，则这条裂隙的连续系数δ为1。统计域内的连续系数可用来表征一定面积域内的一组裂隙的连续系数。设统计域为正方形，面与裂隙走向垂直，见图1。

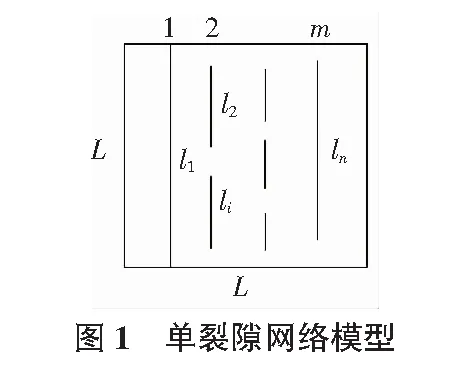
则正方形统计域内的连续系数可由式(1)求出。

(1)

其中，li为单个裂隙长度；n为统计域内裂隙总条数；m为裂隙组总行数；L为统计域边长。

在现场裂隙统计中发现，所测得的连续系数的大小不仅与选取的代表性面域有关，还与统计域面积的大小有密切关系。如果所选定的统计域面积过小，则连续系数的随机波动性将会非常大，数值没有固定的总趋势，可以突然变为0，有时甚至可接近于1。统计可知当统计域面积的边长为裂隙平均迹长的3倍～5倍时，连续系数则趋于稳定，故此时的统计域就可定义为可信域，据此可确定合理统计域的面积大小。在区域范围内对裂隙网络格局的形成、风化作用加速及地下水运移起控制作用的裂隙组称为控制性裂隙组，由各控制性裂隙组所奠定的裂隙场网络系统，一般为分布较均匀的规律性裂隙场网络系统。连续系数只是确定了一组裂隙的发育情况，它们互不相交，只是一个独立的系统，它们之间没有通路联系，故它们的连通系数δii=0，连通度亦为0。若控制裂隙场网络系统包含两组控制性裂隙组，则其连通度不仅与两组裂隙的连通系数δij有关，还与裂隙相互连接排列形式有关，裂隙相互交联的数量占裂隙总量越多，说明裂隙场网络连通性较好，因此可以用连通百分率表示裂隙交联相关度。若裂隙场网络模型由三组或三组以上的控制性裂隙组组成，则应将裂隙组分解为两两相交子网络模型分别计算连通度，最后将计算结果叠加起来计算出裂隙场网络模型连通度,如图2所示。

确定各控制性裂隙组的连续系数后，就可以得出统计域内裂隙组间连通系数δij，因δij与δji相等，故不重复计算，当i=j时，δij为0，进而根据两控制性裂隙组连通百分率求出连通度φ。公式如下：

δij=δi×δj

(2)

(3)

2 大孤山场地裂隙网络模型分析

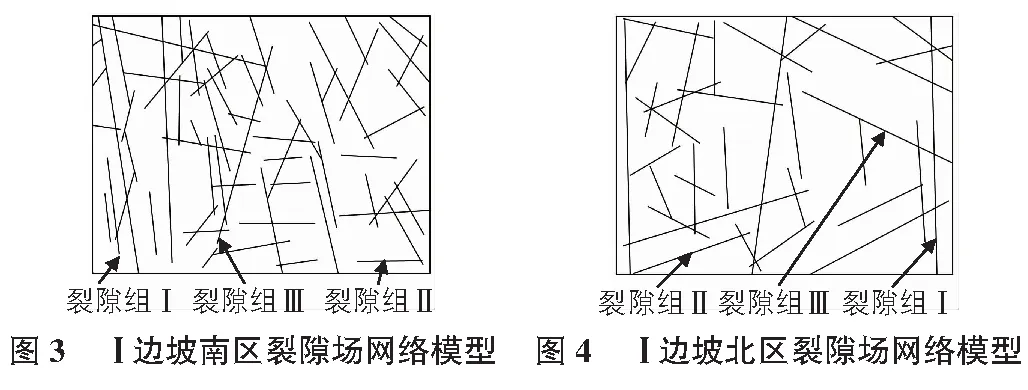
由区域构造特征可知，大孤山裂隙场主要是在三条断层的影响下形成的，裂隙非常发育，排列较杂乱，我们对大孤山地区不同构造分区进行边坡岩体裂隙实测后，建立了岩质边坡裂隙场网络模型(见图3～图7)，裂隙场模型总体反映出裂隙主要由三组控制性裂隙组组成，分别为裂隙组Ⅰ、裂隙组Ⅱ、裂隙组Ⅲ，裂隙组数与此地区构造活动造成三条大断层的应力场环境比较吻合。

根据各分区裂隙场网络中裂隙平均迹长大约为3m，故可确定模型统计面域为9m×9m，选取的统计面域也能较好的反映各分区裂隙分布特征。统计裂隙后对各分区进行了连通度计算，经验系数取1.0，表1列出了部分计算结果。

从表1分析结果可知，裂隙场网络模型计算结果反映出该区岩质边坡裂隙场网络连通度具有不均匀性和各向异性的特点。

Ⅰ边坡南区裂隙组受底部挤压断层和爆破震动影响各组裂隙交联度很好，连通性较好，连通度为0.51。此处裂隙错综复杂，分布较密集，隙宽较大，最宽的可达10cm，风化剧烈，裂隙结构面很粗糙，并且分布有风化强发育带，凸出岩体具有沿连通度高的岩溶发育带滑动的趋势；

Ⅰ边坡北区裂隙主要是在正断层影响下，由两条剪切裂隙派生出很多的张裂隙网络，剪切裂隙连续性很好，迹长也较长，且剪切裂隙结构面较粗糙，但整体连通性一般，在漫长风化历史过程中整体风化不太严重，只是在局部可见风化剧烈的表象，但此处的正断层附近的较破碎岩体具有沿裂隙场连通度较高的剪切面滑动的趋势；

表1 大孤山各区连通度计算结果

而Ⅱ边坡区裂隙是受顺层断层影响，裂隙场网络主要由两条控制性裂隙组组成，裂隙压密后隙宽较小，裂隙发育较好，连通性较好，切割的岩体风化迹象不太明显，由于裂隙场强度较高，所以边坡还是存有潜在危险性，有可能沿裂隙场连通度较高的断层结构面发生滑动；

Ⅲ边坡区裂隙主要由竖直张裂隙控制，裂隙整体连通性不太好，受风化影响较小，只是在局部连通较好的裂隙场中风化较剧烈，没有明显的滑动优势结构面；

Ⅳ边坡区裂隙组排列杂乱，分布不均不密集且相互联系很弱，其连通性很小，风化不明显，也没有发现潜在的滑动弱面。

最终结果表明结合构造特征和裂隙发育特性裂隙场网络模型在探讨岩质边坡风化和稳定性方面具有一定的实用性。裂隙连通性越好，风化程度越剧烈，同时在断层发育带，裂隙连通性较好，岩体风化薄弱带的裂隙场强度较高，而风化剧烈的薄弱带又是岩体滑动优势结构面的场所，这些都表明裂隙场连通度高的区域通常存有滑动优势结构面。

3 结语

1)岩质边坡裂隙场内部裂隙连通性越好，风化作用越剧烈，而裂隙连通性主要受裂隙发育的组数、方向、各组裂隙的密度、迹长、裂隙连通系数及裂隙排列方式等因素控制，这些裂隙就组成一个裂隙网络系统。而一个统计域内的裂隙网络模型主要由控制性裂隙组控制。由控制性裂隙组支配的裂隙场连通程度就可以用连通度定量表示。

2)对大孤山地区5个边坡裂隙实测后建立裂隙网络模型，模型分析结果表明连通度理论对裂隙场定量分析、边坡风化程度和潜在优势滑动面判定具有很好的指导意义。

[1] 姚爱军，薛廷河.复杂边坡稳定性评价和工程实践[M].北京：科学出版社，2008:5-7.

[2] 王 沁.时间序列的确定性分析[M].西安：西安交通大学出版社，2008:11-15.

[3] 沈明荣,陈建峰.岩体力学[M].上海：同济大学出版社,2006:12-15.

[4] 徐耀鉴.岩石学[M].北京：地质出版社,2007:16-19.

[5] 周维垣,刘元高.含裂隙组岩体的稳定问题[J].岩土力学,2003，10(24):13-15.

[6] 碳酸盐岩的裂隙网络连通度及其对岩溶的控制[J].地球科学，1991，1(16)：71-77.

Discussion on stability of fractured rock slope

YANG Zhi-qiang

(PingdingshanBranch,BeijingHuayuEngineeringCo.,Ltd,Pingdingshan467002,China)

This paper establishes the fracture field network model and mainly discuss the stability in the fracture rock slope, the results show that the greater of the connectivity degree, the more serious of the weathering, and the slope is more likely to fail along the potential weak sliding surface where the connectivity degree is high.

fracture rock slope, stability, connectivity degree

1009-6825(2014)13-0066-03

2014-02-22

杨志强(1985- )，男，工程师

TU413.62

A