基于反馈线性化的直驱风力发电机组控制系统

张文秀， 武新芳， 孙 娟

(1. 南京理工大学 能源与动力工程学院，江苏 南京 210094;2. 上海电力学院 能源与机械工程学院，上海 200090)

0 引 言

随着化石能源的不断消耗，以风能为代表的可再生能源受到了世界各国的广泛关注并得到了快速发展。截止2011年底，全球风电装机总容量达到237669MW，占全球总发电量的2.5%。2010年开始，中国已经取代美国成为全球风电装机容量最大的国家[1]。风力发电技术成为了国内外研究的热点。

控制技术是整个风电系统的关键技术之一，研究风电系统高性能的优化控制方法，可提高机组能量装换效率、输出电能质量以及可靠性[2]。风电系统是一个复杂的非线性系统。风速波动范围宽、机械阻尼的影响及空气的气动力特性等造成了系统的控制困难[3]。传统的控制方法在实现高精度控制上已显不足，在风速大范围扰动下，仅仅基于某一特定工况点附近线性化的模型所设计的控制器不能满足控制性能要求。

近年，基于反馈线性化思想的非线性控制理论取得了很大进展，成功解决了电机驱动、电力系统等的非线性控制问题[4-7]。不同于局部线性化方法借助与不同工况点的线性近似，反馈线性化可以在大范围内实现精确解耦线性化，从而用线性最优控制实现最大风能捕获，同时也能改善系统的动态特性。本文基于反馈线性化理论，建立了直驱风电机组模型，设计了非线性控制器，控制风电机组能在最大功率曲线上运行，并进行仿真分析。仿真结果验证了所提出的控制策略的有效性。

1 直驱风电机组模型

1.1 空气动力学模型

由空气动力学的Betz理论[8],风力机的输出功率为

(1)

输出转矩为

(2)

式中：ρ——空气密度；

R——风轮半径；

ω——风力机转速；

λ——叶尖速比；

β——桨距角；

Cp(λ，β)——风能利用系数。

1.2 传动系统模型

直驱风电机组省去了传统风机中的齿轮箱，风力机转轴直接与发电机转子相连。为简化分析，忽略传动系统的柔性和损耗，则直驱型同步发电机组的轴系动态方程可用一阶动态微分方程表示[9]，如式(3)所示。

(3)

式中：Te——电磁转矩；

Jeq——机组等效转动惯量；

Bm——转动粘滞系数。

1.3 PMSG模型

经过Park变换,可得d、q轴同步旋转坐标系下PMSG的数学模型[10]为

(4)

式中：R——定子电阻；

ud、uq——d轴、q轴的定子电压；

Ld、Lq——定子d、q轴的电感；

id、iq——定子d、q轴的电流；

p——极对数；

φm——永磁体产生的磁通；

ωe——转子旋转的电角速度，ωe=pω。

本文将发电机的终端等效成由一固定电感Ls和可变电阻Rs的负载，其中Rs是控制变量，其阻值随着变换器的控制脉冲占空比的变化而变化[11]。直驱风电机组的等效控制模型如图1所示。

图1 直驱风电机组的等效控制模型

2 反馈线性化原理

反馈线性化是设计非线性系统反馈控制器的一种方法，主要思想是利用微分几何工具，通过非线性反馈和同胚映射，将非线性系统全部或部分转换为线性系统[12]。它主要通过状态反馈和坐标变换，得到精确线性化，在整个状态空间都有效，这与传统的线性化方法只在系统工况点附近进行线性化有很大的区别，具体的过程如下。

设有单输入输出的仿射非线性系统[13]为

(5)

式中，x是状态向量，f(x)和g(x)为矢量函数。

如果非线性系统的相对阶与系统阶相等，那么系统将能够通过选定一个坐标闭环，全局线性化为一个线性系统，反之，则可实现部分线性化。

选择坐标映射,得

z(x)=[h(x) Lfh(x) … Lfn-1h(x)]T

(6)

则系统变换为

(7)

式中，υ为线性化系统虚拟输入变量向量，系数矩阵A、B、C分别为

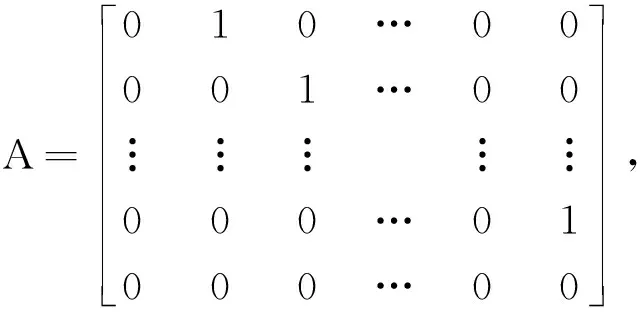
系统线性反馈化控制的基本思想是反复对输出变量y求导，直到y的表达式中出现有输入变量u为止，然后再设计u来抵消非线性项。

首先对输出变量y求导，得

(8)

如果上式中的Lgh(x)≠0，则y的表达式中包含输入变量u,此时可取输入量为

(9)

就可得到y与v的线性控制关系y=v。反之，如果Lgh(x)=0，则继续对y求导，直到LgLfn-1h(x)≠0为止，此时有

(10)

可得到原非线性系统的控制律为

(11)

由上式可以看出，一旦v确定，控制量u也随之确定。

3 非线性控制器设计

3.1 系统控制目标

风电机组的控制目标主要是在额定风速以下，实现最大风能捕获，额定风速以上，机组按恒功率方式运行。对于特定的风力机，都有一条特定的最优的转速-功率曲线，最优功率曲线可以通过实验确定，生产厂家可以将最优功率曲线整定进系统，风电机组的功率控制目标，就是使得机组运行在最优功率曲线上[14]。本文以最优转速yref=ωref作为转速参考值，控制系统通过调节可变电阻Rs的大小，实现风能最优功率的追踪控制。

3.2 直驱风电机组的仿射模型

(12)

(13)

h(x)=ω

(14)

3.3 线性化条件检验

计算系统的相对阶，输出函数关于f(x)和g(x)的Lie导数为

Lfh(x)=d1v2+d2vx3+d3x32-d4x2，

LgLfh(x)≠0。

由于LgLfh(x)≠0，n=1,所以系统的相对阶为2，而系统阶为3，故只能实现部分线性化。

3.4 控制器设计

将系统的数学模型部分线性化，首先要进行坐标变换[15],以满足可微分条件。引入Z坐标，非线性Z坐标变换为

(15)

经过Z坐标变换的线性系统状态方程为

(16)

设yref为输出y要跟踪的参考输入，为了使系统在稳态时无静态偏差，引入误差ε=yref-y，此时误差的积分量为

两边积分得

uv=-k1z1-k2z2-k3ε，由反馈线性化原理可知，非线性系统的输入u与控制输入uv的关系为

(17)

式中，uv通过选取适当加权阵Q=diag(400,400,0),R=1。利用MATLAB函数care()求解代数Riccati(黎卡提)矩阵[K,P,L]=care(A,B,Q,R)求得[16]，其中L是闭环状态方程参数矩阵特征值，P是代数黎卡提方程的解，K为最优反馈线性矩阵。求解结果为

uv=-4000z1-150z1-30000ε

本文设计的线性系统的状态反馈框图如图2所示，状态反馈部分为Lie导数Lf2h(x)和LgLfh(x)。

图2 线性系统状态反馈控制框图

4 仿真分析

为了验证本文基于反馈线性化理论设计的非线性控制器的正确性和有效性，利用MATLAB/Simulink仿真平台搭建了直驱风电机组模型，分别采用阶跃风速和随机风速进行仿真以验证系统保持最优功率运行的能力。仿真主要参数如表1所示。

表1 仿真参数

应用反馈线性化控制的功率曲线追踪框图如图3所示。

图3 基于直驱风电机组的反馈线性化控制框图

4.1 阶跃风速

在t=25s时，风速由7m/s阶跃到9m/s时的仿真结果如图4所示。

图4 阶跃风速下仿真结果

由图4可看出，当风速上升时，由于风力机所受的力矩变大，风轮转速随之上升，风能利用系数基本维持在0.47～0.48，与叶尖速比的变化趋势吻合。

4.2 风速扰动

风速扰动下仿真结果如图5所示，平均风速为8m/s,波动范围为5～11m/s。

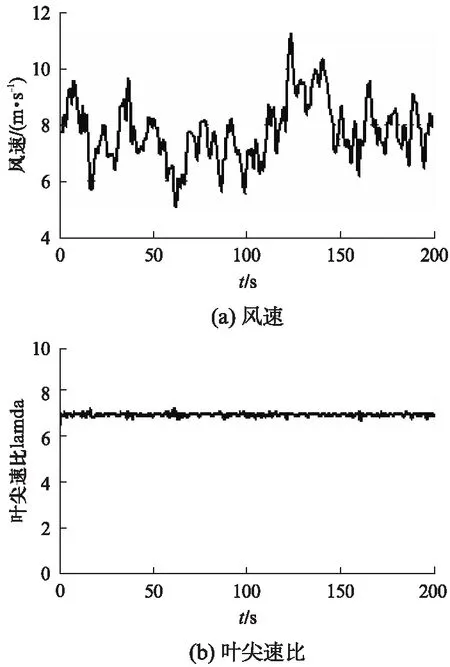
图5 风速扰动下仿真结果

由图5可看出，在风速扰动情况下，控制器响应迅速，使机组的输出在其后的输出超调量很小，风轮转速跟随变化，由于建模过程中忽略了传动系统的柔性和损耗，机械能由风力机传递到发电机转子，同时发电机也是按照理想电机的条件进行建模，实际风机模型中存在的如机械摩擦造成的迟滞现象并未表现得明显，风能利用系数在0.476上下幅值内小范围波动，叶尖速比恒定在7附近，控制效果较好。

基于反馈线性化理论设计的直驱风电系统在风速阶跃变化和扰动时，响应迅速且平稳，超调量很小，具有较强的鲁棒性，风轮转速能够动态跟踪风速的变化，风能利用系数Cp和叶尖速比λ在最优值附近波动，即表明机组运行在最优功率曲线上，这有利于风电机组的良好运行和降低负荷波动引起的不良影响。仿真结果验证了所提出控制策略的正确性及所设计的控制器良好的性能，能实现风电机组最优功率的跟踪控制，具有良好的闭环控制效果。必须指出的是，所提出的控制策略在机组起始运行阶段响应较慢，稳定性不太好，这还需要进一步的深入研究。

5 结 语

为了提高直驱风力发电机组的控制性能，使得风电机组能运行在最优功率曲线上，本文提出了一种反馈线性化控制策略，建立了风电机组各个组成部分的模型，并在所设计出的对应控制器的基础上进行仿真验证。仿真结果证明该控制策略对风速变化具有很好的鲁棒性，并且具有较好的动态控制性能这对于实际风力发电系统控制器的优化设计和研发有一定的参考意义。

【参考文献】

[1] Global Wind Energy Council. Global wind report-annual market update 20011[R]. Brussels Belgg-ium： Global Wind Energy Council, 2012.

[2] 李元龙，朱芸，纪志成.风能转换系统优化控制策略综述[J].微特电机，2009,2(2)： 59-63.

[3] SENJYU T, SAKAMOTO R, URASAKI N, et al. Output power leveling of wind turbine generator for all operating regions by pitch angle control[J]. IEEE Transactions on Energy Conversion, 2006, 21(2)： 467- 475.

[4] LEE T S. Input-output linearization and zero-dy-namics control of three-phase AC/DC voltage-source converters[J]. IEEE Transactions on Power Electronics, 2003,18(1)： 11-22.

[5] 石峰，查晓明.应用微分几何理论的三相并联型有源电力滤波器解耦控制[J].中国电机工程学报，2008,28(15)： 92-97.

[6] 乐江源，谢运祥，张志，等.三相有源电力滤波器精确反馈线性化空间矢量PWM复合控制[J].中国电机工程学报，2010,30(15)： 32-39.

[7] 江道灼，张振华.单相H 桥级联静止同步补偿器反馈线性化解耦控制[J].电网技术，2011,35(11)： 74-79.

[8] 叶杭冶.风力发电机组的控制技术[M].北京： 机械工业出版社，2006.

[9] 陈浩，胡晓波，严干贵，等.直驱永磁风力发电机组低电压穿越的协调控制策略[J].电网技术，2013,37(5)： 1466-1470.

[10] ARKADAN A A, VYAS R. Effects of toothless stator design on dynamic model parameters of permanent magnet geneators[J]. IEEE Transactions on Energy Conversion, 1993, 8(2)： 243-250.

[11] NICOLAS A C, EMIL C, ANCA D H, et al.Robust multi-model control of an autonomous wind power system [J]. Wind Energy, 2006, 9(5)： 399- 419.

[12] 林辉，王永宾，计宏.基于反馈线性化的永磁同步电机模型预测控制[J].测控技术，2011，30(3)： 53-57.

[13] JEAN-JACQUES E S. Applied nonlinear control [M]. Beijing： China Machine Press, 2004.

[14] 严干贵，魏治成，穆钢，等.直驱永磁同步风电机组的最优功率控制[J].电机与控制学报， 2009, 1(13)： 56-60.

[15] INLIAN M, ANTONETA I B, NICOALS A C, et al.Optimal control of wind energy systems[M]. London： Springer, 2008.

[16] 刘豹.现代控制理论[M].北京： 机械工业出版社，2000.