基于景观生态学的人口空间数据适宜格网尺度研究——以山东省为例

李月娇，杨小唤，王静

（1.中国科学院地理科学与资源研究所资源环境信息系统国家重点实验室，北京 100101；2.中国科学院大学，北京 100049；3.宁夏地震局，宁夏 银川 750001）

0 引言

近年来，国内外学者在不同地区建立了不同尺度的空间人口数据库，但以往的研究是在省级、市级、县级或是格网尺度上进行的单一尺度研究，而地理学研究对象格局与过程的发生、时空分布、相互耦合等特性都有尺度依存性［1］，人口的空间分布亦具有一定的尺度依赖性［2］，不同尺度上人口空间分布格局的特征往往不同。因此，若要更确切、真实地揭示人口空间分布规律，需要从不同尺度上对人口空间分布格局进行分析［3］。

不同格网尺度表达人口空间分布适宜性的研究国内外关注较少。叶靖建模生成20m至1km系列的浙江省义乌市格网人口数据，运用空间分析和数理统计方法，通过比较不同的格网人口与乡镇统计人口误差，分析人口空间化的格网尺度效应，充分证明了人口空间化数据并不是尺度越细精度越高，不同空间化方法有各自的适宜尺度［4］。杜国明等在对沈阳市人口统计数据进行空间化的基础上，从统计特征、空间自相关性和空间格局三方面分析人口密度在10种粒度下的异同，证明了人口密度尺度效应的存在［5］。王静运用空间自相关方法和统计相关分析方法，比较山东省市级、县级、1km 3个尺度人口分布的空间自相关性及其与环境—经济因子的统计相关性，发现从不同尺度对人口的空间分布格局进行分析，得到从宏观到微观不同详细程度的信息，且不同尺度上人口空间分布格局特征不同［3］。

本文基于GIS技术，利用山东省2005年土地利用数据和人口统计数据生产100m、200m、300m、400m、500m、600m、700m、800m、900m、1km 10个格网尺度人口空间数据，引入景观生态学的相关指数和方法，分析人口分布景观格局随着人口空间化尺度的变化趋势，对山东省不同格网尺度表达人口空间分布的适宜性进行科学分析，可以为指导人口空间数据的生产和应用提供科学依据，也可为今后其他类型的数据空间化处理提供借鉴，最终为人文科学和自然科学的融合研究、政府相关决策、灾害防治和灾情评估等提供高精度的数据支持。

1 数据源与研究方法

本文使用的原始数据为山东省2005年县级人口数据（源于山东省统计年鉴2005，Excel格式）和山东省2005年土地利用数据（源于中国科学院遥感应用研究所，grid格式），其中土地利用数据为百分比数据，即1km2内某种土地利用类型所占比例，包括耕地、城镇用地、农村居民点3种土地利用类型。

本文选用传统的基于土地利用／覆被的人口数据空间化方法进行人口格网数据的生产［6，7］，假设研究区内同一土地利用类型内人口均匀分布，以耕地面积、城镇居民地用地面积、农村居民点用地面积为自变量，县（市、镇）统计人口为因变量，建立回归模型，推演城镇居民点用地、农村居民点用地人口分布系数，模拟县级人口分布模式，模型的一般形式为：

式中：Pi为某地区第i县（市、镇）的统计人口数；aj为j类土地利用的人口分布初始系数（人／km2）；Sij为i县（市、镇）j类土地利用的面积（km2）；n＝3代表3种土地利用类型；根据无土地则无人口的原则，常数项b为0。

模型假定某分区同一土地利用类型人口分布系数相同，因此人口空间数据总数与统计人口数据必然存在一定的误差。为确保各县（市、镇）内所有格网中的人口数据之和与实际统计人口相等，通过平差对各县（市、镇）的人口分布初始系数aj进行校正，得到校正后的人口分布系数aij。校正公式为：

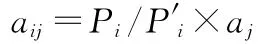
式中：aij表示i县（市、镇）j类土地利用的人口分布系数（人／km2）；校正系数为Pi／P′i，Pi为i县（市、镇）统计人口数据，P′i为根据模型反算的i县人口数据。由此得到各县耕地人口分布系数、城镇居民点用地人口分布系数、农村居民点用地人口分布系数。

假设格网人口与县级人口具有相同的分布模式，将县级人口空间分布模型应用于格网尺度，以城镇居民点用地人口分布系数、城镇居民点面积、农村居民点用地人口分布系数、农村居民点用地面积反算格网人口，计算公式如下：

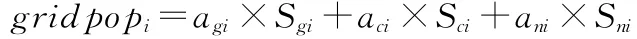
式中：gridpopi为某栅格i上的人口值；agi、aci、ani分别为栅格i上的耕地人口分布系数、城镇居民点用地人口分布系数和农村居民点用地人口分布系数；Sgi、Sci、Sni分别为栅格i上的耕地面积、城镇居民点面积和农村居民点面积。

本文使用Fragstats软件计算人口的景观格局指数，共选取了13个景观指标（表1）［8－17］。

表1 本文选取的景观指标Table 1 The landscape indicators selected in this paper

2 景观指数随尺度的变化

2.1 景观指数随尺度变化有规律波动，并出现拐点

斑块数量（NP）、加权平均斑块面积（AWMPS）、斑块面积变异系数（PSCV）、形状指数变异系数（SICV）、香农多样性指数（SHDI）和香农均度指数（SHEI）6个景观指数随尺度变化有规律波动，并出现拐点（图1）。

NP随尺度变化而波动，在400m和800m尺度时有明显的极大值拐点，分别为22 934和22 152，其余尺度间差异较小。图2为1km、400m、300m尺度下某一小区域的人口聚居图，一个较大的人口聚居区被其他小的人口聚居区包围。在400m尺度，一些被隐藏在其他聚居区中的小的聚居区显现出来，人口聚居区数量最多，人口景观最破碎，可见400m尺度人口景观密度所反映的人口分布信息最全面、最细致。

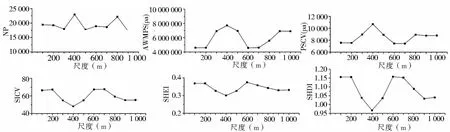
图1 有规律波动式景观指数的变化趋势Fig.1 Trend figure of regular fluctuation landscape indices

图2 1km、400m、300m人口聚居图Fig.2 Population map of 1 km，400 m，300 m

加权平均斑块面积（AWMPS）和斑块面积变异系数（PSCV）随尺度变化呈正弦式波动，在各尺度之间差异较大，且在400m尺度时达到极大值。这表明，在400m尺度时人口聚居区的加权平均斑块面积达到最大，且人口聚居区之间的面积差异最大。400m尺度时，一些小型人口聚居区从较大的人口聚居区中分离出来而得以显现，加大了人口聚居区面积的变异，同时人口景观中的优势人口聚居区吞噬周围小的人口聚居区而扩张，使得人口聚居区加权平均面积增加。

形状指数变异系数（SICV）随尺度变化呈正弦式波动，在各尺度之间差异较大，在400m尺度时达到最小值，这表明在400m处人口聚居区形状指数的差异最小，人口聚居区倾向于最简单分布或复杂分布。

香农多样性指数（SHDI）和香农均度指数（SHEI）随尺度变化均呈正弦式波动，且均在400m尺度达到极小值，在该尺度优势人口聚居区类型吞噬了周围小的人口聚居区斑块，具有更大的优势性，从而增加了各人口聚居区类型的非均衡分布程度。400m尺度人口景观密度不仅较全面细致地反映了人口分布信息，且反映的信息也较完整。

2.2 景观指数随尺度变化下降

聚合指数（AI）、蔓延度指数（CONTAG）、斑块结合度（COHESION）均随尺度的变大而减小（图3）。这表明，随着尺度的增加，景观中不同斑块之间的团聚性减小，斑块之间的粘合程度和连通性减小，人口聚居区的集聚程度减小。蔓延度指数在200～600m之间存在一个尺度变化域，且在400m尺度处存在拐点。

图3 下降式景观指数变化趋势Fig.3 Trend figure of descending landscape indices

2.3 景观指数随尺度呈无规律变化

总边缘长度（TE）、面积加权平均形状因子（AWMSI）、景观丰度（PR）、散步与并列指数（IJI）随尺度变化无规律波动（图4）。总边缘长度随尺度变化缓慢波动，在900m～1km和300～500m为两个低值区域，在600～800m及100～200m存在两个高值区域。总边缘长度是形状和斑块数量的函数，在400m尺度时斑块数量最大而总边缘长度较小，说明在该尺度虽然斑块数量的增加使得总边缘长度增大，但同时斑块形状也趋于简单，使得总边缘长度减小。这表明，400m尺度时，虽然人口聚居区的数量较多，但由于各聚居区的形状较简单，人口聚居区的总边缘长度不大。面积加权平均形状因子虽然随尺度呈无规律变化，但在400m处有极小值，这与上文分析的400m尺度总边缘长度较小、人口聚居区数量较多、可能形状复杂程度小相吻合。景观丰度、散步与并列指数随尺度变化而波动，且都在400m尺度处有拐点。

图4 随尺度变化无规律波动Fig.4 The irregular fluctuation of landscape indices

3 结论

在用传统的基于土地利用／覆被的人口数据空间化方法进行人口空间化的过程中，并不是尺度越精细所能表达的信息越细致、完整。本文利用景观生态学的相关指数和方法，探索不同格网尺度表达人口空间分布的适宜性。研究发现：随着尺度减小，山东省人口分布景观格局的变化趋势为：斑块的团聚程度、粘合度增大，人口聚居区的集聚程度增大；400m尺度是该区域人口空间化数据的特征尺度，此时人口聚居区的数量最多，且各聚居区之间的面积差异最大，形状最简单，景观中优势人口聚居区类型的优势最大，各类型间非均衡程度最高。400m是一个人口尺度变化上的特征点，所反映的人口分布信息最细致且完整性好。由此可得，在进行山东省人口空间化的过程中，400m是一个比较适宜的尺度。

［1］ 李双成，蔡运龙.地理尺度的转换若干问题的初步探讨［J］.地理研究，2005，24（1）：11－18.

［2］ 杜国名，张树文，张有全.城市人口密度的尺度效应——以沈阳市为例［J］.中科院研究生院学报，2007，24（2）：186－192.

［3］ 王静，杨小唤，石瑞香.山东省人口空间分布格局的多尺度分析［J］.地理科学进展，2012，31（2）：176－182.

［4］ 叶靖，杨小唤，江东.乡镇级人口统计数据空间化的格网尺度效应分析［J］.地球信息科学，2010，12（1）：40－47.

［5］ 杜国明，张树文，张有全，城市人口分布的空间自相关分析——以沈阳市为例［J］.地理研究，2007，26（2）：383－390.

［6］ 杨小唤，江东，王乃斌.人口数据空间化的处理方法［J］.地理学报，2002，57（增刊）：70－75.

［7］ YANG X H，HUANG Y H，DONG P An updating system for the gridded population database of China based on remote sensing，GIS and spatial database technologies［J］.Sensors，2009，9（2）：1128－1140.

［8］ 蔡博峰，于嵘.景观生态学中的尺度分析方法［J］.生态学报，2008，28（5）：2279－2287.

［9］ 杜秀敏，黄义雄，叶功富.厦门市景观格局的尺度效应分析［J］.测绘科学，2010，35（4）：71－74.

［10］ 吕一河，傅伯杰.生态学中的尺度及尺度转换方法［J］.生态学报，2001，21（12）：2097－2105.

［11］ 吕志强，吴志峰，张景华.基于最佳分析尺度的广州市景观格局分析［J］.地理与地理信息科学，2007，23（4）：89－92.

［12］ 邬建国.景观生态学——格局，过程，尺度与等级［M］.北京：高等教育出版社，2000.

［13］ 肖笃宁.景观生态学［M］.北京：科学出版社，2003.

［14］ 张娜.生态学中的尺度问题：内涵与分析方法［J］.生态学报，2006，26（7）：2340－2355.

［15］ 赵磊.基于多源遥感数据的区域景观格局尺度效应［J］.遥感应用，2009（8）：54－61.

［16］ PETERSON G D.Scaling ecological dynamics：Self－organization，hierarchical structure，and ecological resilience［J］.Climatic Change，2000，44（3）：291－309.

［17］ VELDKAMP A，KOK K，DE KONING G.Multi－scale system approaches in agronomic research at the landscape level［J］.Soil and Tillage Research，2001，58（3－4）：129－140.