基于GIS的时空节点规划与优化方法研究

刘钊，罗智德，张耀方，高培超，谢美慧

（1.清华大学地球空间信息研究所，北京 100084；2.中国科学院水利部水土保持研究所，陕西 杨凌 712100）

0 引言

社会生活中的一些活动需要人与人之间会面才能完成，例如应急救灾中的物资发放、物流运输中的货物交接、校车接送学生、医疗救护车接收病人等；这些活动都有一个活动发起者（如物资车、送货员、校车等）和至少一个活动参与者（如灾民、顾客、家长等），为使活动顺利展开并尽可能提高效率，往往需要对会面的时间和地点提前预约。本文将此类活动中预约的时间点和空间位置称为时空节点。

在上述活动中，规划活动发起者的空间移动路径可用旅行商问题（TSP）的算法求解，即设计一条从确定起点出发，途经所有目标节点并只访问一次，最终回到出发点的最短路径［1，2］。众多学者对此进行了深入研究，已有许多适用于具体问题的成熟算法［2］和软件产品，如遗传算法［3］、蚁群算法［4］、神经网络算法［5］等。在现有的GIS软件如ESRI、Intergraph中，已嵌入了一些成熟的最短路径算法［6］，得到最短路径后，活动发起者根据路网属性推断到达每个目标点的时间，实现对时空节点的预约。旅行商问题的算法从活动发起者的角度规划线路，较少考虑活动参与者在时间和空间上的限制条件，其得到的方案仍然可以进一步优化。

本文基于时间地理学框架，将活动发起者提前预计的活动轨迹表达为时空路径，根据活动参与者时空约束类型的不同分别将其表达为时空路径、圆柱和棱镜；在此基础上求解发起者和参与者之间的时空交集，以规划双方会面的时空节点并优化活动发起者的行进线路。

1 研究方法

1.1 时间地理学工具

时间地理学将个体作为研究主体，在时空背景下研究其行为，通过分析人类活动的时空约束条件，建立一个动态描述和解释行为活动的框架［7－9］，认为个体活动有三类限制：能力限制、组合限制和权威限制［9］，某项具体活动只能出现在指定的地点和时间段，个体能借助交通实现用时间换取空间的目标［8，10］。时空路径和时空棱镜是实现时间地理理论的两个最核心的工具［11］。

时空路径记录了个体在时间和空间上的移动，由控制点和路径段落构成，控制点是已知具体位置和时间属性的点，路径段落是点与点之间的连线［11］。图1为时空路径的示意图，其中的垂直段落代表个体在该时段内停留在特定地点，倾斜段落代表个体在该时段内有位置上的移动。时空路径详尽地记录了个体活动的时空属性［12］。不同个体能见面需要他们的时空路径有交集，图1中的个体A和个体B于T2时刻在Pi处相遇。本文用时空路径表达活动发起者和严格限定位置的参与者的时空约束。

时空棱镜表达了在已知起点、终点、出发时刻、结束时刻、最高旅行速度等限制条件的情况下，个体所能到达的所有时空区域［13］，时空棱镜的边界就是个体所能到达的最大时空范围［14］。图2为时空棱镜的示意图，L1是起点、L2是终点，时间窗口是t1到t2［15］。若某活动在时空棱镜内发生，如活动a，时空棱镜所表示的个体即可参与其中；若某活动在时空棱镜以外发生，如活动b和c，则时空棱镜所表达的个体将不能参与其中［15］。本文用时空棱镜表达限定可用时间起点和终点的活动参与者的时空约束。

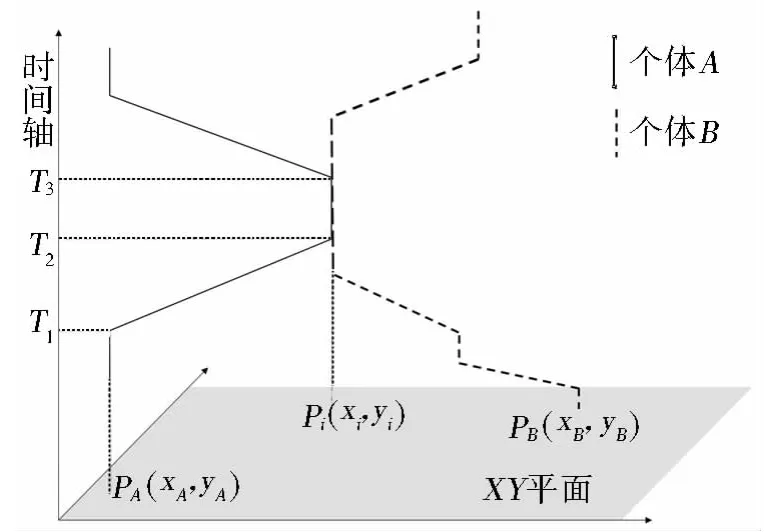
图1 时空路径示意Fig.1 Space－time path

图2 时空棱镜和潜在路径区域［15］Fig.2 Space－time prism and potential path area

Yu、Shaw等学者对时间地理学工具进行了拓展，用于表达虚拟空间的活动［14，15］。用一条垂直的时空路径表示有线网络接入点，以无线网信号发射点的空间位置为圆心，最大影响距离为半径作圆，再沿时间轴拉伸形成圆柱，用于表示无线网络的时空可达性［15］。本文用此方式表达限定可用时间长度的活动参与者的时空约束。

1.2 基于时间地理学的时空约束表达

本文将活动发起者的时空约束表达为时空路径，将活动参与者的时空约束分为三类，分别用时空路径、圆柱和棱镜表达。

活动发起者的行进线路在时空环境中抽象为由控制点和点之间的片段组成的时空过程对象，将这些时空对象用三维方式表达，构成一条时空路径。设活动发起者开始行动的时间为tS，预计结束的时间为tE，规划路径中会经过的点作为控制点，每个点都有对应的x、y坐标和预计到达该点的时间t，则控制点序列可以表示为［9－11］：

点与点间由直线片段连接，每个片段表达了发起者在该时段内的时空属性变化［11］；每个控制点既是上一片段的结束，也是下一片段的开始。片段的性质由首尾的两个控制点决定，由式（2）和式（3）描述［10，11］。式（2）表示Ci和Cj两个相邻控制点间的片段，片段Sij除了控制点Ci和Cj外的其余部分的横坐标、纵坐标和时间属性由线性插值获取。

对于严格限定位置的参与者而言，其空间位置保持不变。此类参与者的时空约束类似于文献［15］中有线网络的时空约束，可表达为一条垂直的时空路径，如式（4）所示。式中，x0、y0表示参与者的横、纵坐标，ts、te为该个体可支配时间的起点和终点。该路径位于参与者所在的平面位置上，且沿着时间轴在可支配时间内延伸。

对于限定可用时间长度的活动参与者而言，其位置是变化的，但必须满足可用时间长度的限制。此类活动参与者的时空约束类似于文献［15］中无线网络的时空约束。在可用的时间范围内，参与者可以到达的空间范围是以其位置为圆心，以最长可达距离为半径的一个圆，将这个圆沿着时间轴拉升，形成一个圆柱。对于落在圆柱体内的任何时空点P（x，y，t）都满足式（5），Δt为可支配时间长度，v是最高旅行速度。考虑到参与者需要返回原位置，其潜在活动区域是以起始位置（x0，y0）为圆心、以r＝v·Δt／2为半径的圆。任意时刻，参与者所处的位置P（x，y，t）距圆心的距离应小于或等于半径r。

限定可用时间起点和终点的活动参与者可以从时间起点出发，在限定时段内活动，在时间终点回到原地。此类参与者的时空约束可用时空棱镜表达，时空棱镜的起点和终点都在参与者起始的位置上，可达空间范围受可支配时间长短和旅行速度的影响。时空棱锥的外边界由起始点Xi、终结点Xj、起始时间ti、终结时间tj、最高旅行速度vij5个条件决定。每个时空棱镜是由前后两个相向圆锥组成的交集，如式（6）［10］所示。前向圆锥表示从起点出发可能到达的所有时空点，后向圆锥表示要在指定时间到达终点，个体可能位于的时空点［16］。前棱锥fi的顶点在出发点，底面位于t＝（ti＋tj）／2处，位于前棱锥体的点X（x，y，t）满足式（7）［10］；后棱锥pj的顶点位于终结点上，底面也位于t＝（ti＋tj）／2处，位于后棱锥中的点 X（x，y，t）满足式（8）［10］。

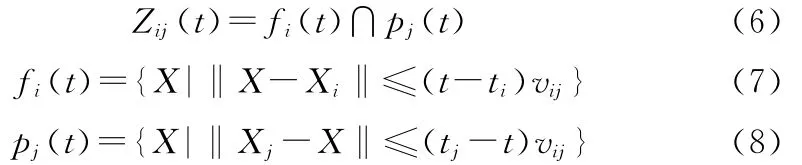
1.3 时空节点的规划和优化

将一个完整的预约活动进行简化：活动发起者通过旅行商算法得到了一条设定的线路，活动参与者拥有自己的时空限制，发起者和参与者需要会面，意味着他们的潜在活动区域有交集，有共同的时空节点。对时空节点的规划就是寻找到既满足活动参与者的时空限制条件，又尽量节约发起者时间成本的会面地点和时间。时间地理学工具的优势在于它将个体的时间维和空间维信息放在同一个框架下进行分析［7，12］。两个个体在时间和空间上有交集，那么他们的时空约束就有共同的时空节点［10］。本文将预约活动双方的时空约束条件用时间地理学工具表达，在此基础上寻找其间的时空交集，确定适合的预约时间和地点，并据此进行线路调整，实现对时空节点的规划和优化。

ArcGIS三维环境中，二维平面坐标X、Y和时间信息T构成了可视化环境中的3个坐标轴。1.2节的时空路径由三维点和三维线段构成，圆柱和圆锥则由三维体构成。寻找潜在的活动时空节点就转化为确定活动发起者的时空路径与活动参与者的时空路径、圆柱、棱镜间的交集。当限定了参与者的活动地点时，联立式（1－4）得到的交点即是可预约会面的时空节点。当限定了参与者的可用时间长度时，联立式（1－3）和式（5），求解出既在活动发起者行进线路上又满足活动参与者的时空约束的时空节点P（x，y，t），即可预约的时间和地点，最先出现的时空节点就是可最早预约的点。当限定了参与者的可用时间起点和终点时，联立式（1－3）与式（6－8），求解出满足式（1－3）和式（6－8）的点P（x，y，t），即可预约的时间和地点，最先出现的点就是可最早预约的点。

如果一个活动只有一个参与者，那么直接求解最早会面的时空节点，即可完成会面过程。如果一个活动有多个参与者，需要在每实现一个参与者的会面后，将该参与者从清单中删除；再以活动发起者所处的位置和时间作为其新的时空路径的起点，根据剩下的参与者的时空约束重新规划活动方案；亦可将新的活动参与者添加进列表，进行整体的规划。通过这种方式确定活动发起者与每个活动参与者会面的时空节点，以实现对整个过程的优化。

2 应用案例

在Visual Studio 2010环境中，利用C＃语言进行代码编写，基于ESRI公司的ArcGIS Engine搭建了原型系统，实现了本文的方法。活动发起者和参与者的时空约束都需进行设置，求解结果以点层的方式分别展现在三维地图和二维平面地图中，同时以文本的方式标注其时空属性。图3是原型系统主界面，用于显示和操作相关的时空数据，道路网络、背景地图、活动参与双方的时空约束等都表达在三维地图中。图4是一个二维地图界面，用于展示求解得到的时空节点的平面位置。

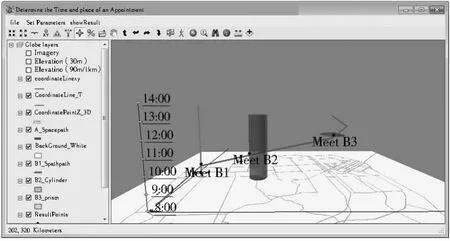
图3 原型系统主界面Fig.3 The main interface of the prototype

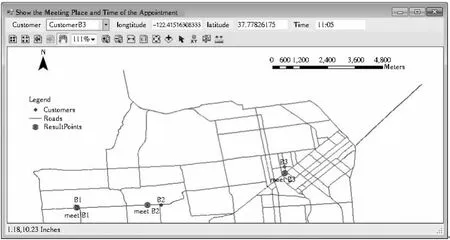
图4 显示预约点的二维平面位置Fig.4 The position of the reservation points showed on a two－dimensional plane

本文利用ESRI公司提供的旧金山城市路网数据和某电子商务网站一次物流配送过程数据，模拟了一个实例。A作为物流配送员，根据最短路径算法得到一条设定的线路，线路上已有一些预期会到达的点和到达该点的时间。本文模拟了3个具有不同时空约束的顾客：B1要求货物送到指定地点，时间上不限定；B2只有20min可用于配合接收货物，最高旅行速度是1m／s；B3只能在11∶00－11∶30配合接收货物，最高旅行速度是1 m／s。将A表达为时空路径，由式（1－3）描述；B1表达为特殊的时空路径，由式（4）描述；B2表达为棱柱，由式（5）描述；B3表达为时空棱镜，由式（6－8）描述；如图3所示。定量化的求解过程在后台运行，求解得到的预约地点和时间分别展示在三维地图（图3）和二维平面地图（图4）中，并以文本的方式标明其时空属性。

由于B1有严格的地点限制，利用本文方法得到的预约时空节点与传统方法一样，没有优化。而对于B2，传统方法不考虑B2对物流配送过程的配合，快递员应该于10∶00将货物送到B2所处位置，而本文方法求解结果表明应该在9∶51在图4所示的位置处会面，随后送货员可以调整线路进行下一个送货任务，实现了对路径的优化。B3不在A设定的线路上，传统方法只能让A将货物送到最临近的区域，时间和具体位置都不易控制；利用本文的方法，在考虑B3配合的情况下，得出应该在11∶05时会面。本案例中，原型系统利用时间地理学工具在GIS环境下实现了对活动预约时空节点的规划和优化；求解得到的时空节点既能满足顾客的时空约束条件，又能尽量节约送货员的时间，便于快递员根据实际送货进度和剩余顾客的时空约束及时调整路线，提高了物流配送的准确度和效率。

3 结论与讨论

针对日常生活中的时间和地点预约问题，本文首先介绍了进行时空节点规划的传统做法即旅行商问题的相关算法。在此基础上，结合GIS技术，将时间地理理论应用于表达活动发起者和参与者的时空约束中，根据最短路径算法解得活动发起者的起始路线，用时空路径表达活动发起者预计的时空轨迹，将活动参与者分为限定位置、限定时间长度和限定时段3类，分别用时空路径、圆柱和棱镜表达。于是，将求解活动双方会面的时间和地点的问题转换为求解双方的时空交集的问题，可在GIS环境下定量地求解。最后，利用ArcGIS Engine开发原型系统，实现了该时空节点规划和优化方法。用模拟数据进行了实例检验，结果显示此方法能够辅助节省活动发起者的时间成本，便于对活动过程的把控和及时对行进路线进行优化和调整。本研究应用于应急救灾、物流管理、旅游等活动中，可辅助决策者对时间和空间预约有更为准确的规划。

本文将活动参与者的时空约束理想化地表达为规则的几何体，现实生活中的个体潜在活动范围还会受到道路、地形、障碍物等因素的限制，而时间约束也是多样的，这些都是下一步需要研究的。在活动发起者设定最初的路线时，如何将每个目标点的时空约束考虑进去，也就是在旅行商问题的算法中加入对参与者的时空约束的分析也值得进一步研究。

［1］ GILBERT L.The traveling salesman problem：An overview of exact and approximate algorithms［J］.European Journal of Operational Research，1992，59（2）：231－247.

［2］ 王剑文，戴光明，谢柏桥，等.求解TSP问题算法综述［J］.计算机工程与科学，2008，30（2）：73－74.155.

［3］ BRAUN H.On solving traveling salesman problems by genetic algorithms［J］.Lecture Notes in Computer Science，1991，496：129－133.

［4］ DORIGO M，GAMBARDELLA L M.Ant colonies for the travelling salesman problem［J］.BioSystems，1997，43（2）：73－81.

［5］ GHAZIRI H，OSMAN I H.A neural network algorithm for the traveling salesman problem with backhauls［J］.Computers and Industrial Engineering，2003，44（2）：267－281.

［6］ CURTIN K M.Network analysis in geographic information science：Review，assessment，and projections［J］.Cartography and Geographic Information Science，2007，34（2）：103－111.

［7］ YU H，SHAW S L.Exploring potential human activities in physical and virtual spaces：A spatio－temporal GIS approach［J］.International Journal of Geographical Information Science，2008，22（4）：409－430.

［8］ NEUTENS T，VAN DE WEGHE N，WITLOX F，et al.A three－dimensional network－based space－time prism［J］.Geographical Systems，2008，10（1）：89－107.

［9］ 赵莹，柴彦威，陈洁，等.时空行为数据的GIS分析方法［J］.地理与地理信息科学，2009，25（5）：1－5.

［10］ MILLER H J.A measurement theory for time geography［J］.Geographical Analysis，2005，37（1）：17－45.

［11］ MILLER H J，BRIDWELL S A.A field－based theory for time geography［J］.Association of American Geographers，2009，99（1）：49－75.

［12］ YU H.Spatio－temporal GIS design for exploring interactions of human activities［J］.Cartography and Geographic Information Science，2006，33（1）：3－19.

［13］ KUIJPERS B，MILLER H J，NEUTENS T，et al.Anchor uncertainty and space－time prisms on road networks［J］.International Journal of Geographical Information Science，2010，24（8）：1223－1248.

［14］ SHAW S L，YU H.A GIS－based time－geographic approach of studying individual activities and interactions in a hybrid physical－virtual space［J］.Transport Geography，2009，17：141－149.

［15］ YU H，SHAW S L.Exploring potential human activities in physical and virtual spaces：A spatio－temporal GIS approach［J］.International Journal of Geographical Information Science，2008，22（4）：409－430.

［16］ DELAFONTAINE M，NEUTENS T，VAN DE WEGHE N.A GIS toolkit for measuring and mapping space－time accessibility from a place－based perspective［J］.International Journal of Geographical Information Science，2012，26（6）：1131－1154.